1．棱镜对光的偏折作用

一般所说的棱镜都是用光密介质制作的。入射光线经三棱镜两次折射后，射出方向与入射方向相比，向底边偏折，虚像向顶角偏移。

[例7]　 如图所示，一细束红光和一细束蓝光平行射到同一个三棱镜上，经折射后交于光屏上的同一个点M，若用n₁和n₂分别表示三棱镜对红光和蓝光的折射率，下列说法中正确的是

A.n₁<n₂，a红光，b蓝光　　 B.n₁<n₂，a蓝光，b红光

C.n₁>n₂，a红光，b蓝光　　 D.n₁>n₂，a蓝光，b红光　

解：由图可知，b光线经过三棱镜后的偏折角较小，因此折射率较小，是红光。

3．光导纤维，海市蜃楼和内窥镜

全反射的一个重要应用就是用于光导纤维(简称光纤)。光纤有内、外两层材料，其中内层是光密介质，外层是光疏介质。光在光纤中传播时，每次射到内、外两层材料的界面，都要求入射角大于临界角，从而发生全反射。这样使从一个端面入射的光，经过多次全反射能够没有损失地全部从另一个端面射出。

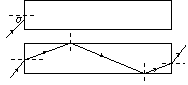[例6]如图所示，一条长度为L=5.0m的光导纤维用折射率为n=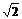的材料制成。一细束激光由其左端的中心点以α= 45°的入射角射入光导纤维内，经过一系列全反射后从右端射出。求：⑴该激光在光导纤维中的速度v是多大？⑵该激光在光导纤维中传输所经历的时间是多少？

解：⑴由n=c/v可得v =2.1×10⁸m/s

⑵由n=sinα/sinr可得光线从左端面射入后的折射角为30°，射到侧面时的入射角为60°，大于临界角45°，因此发生全反射，同理光线每次在侧面都将发生全反射，直到光线达到右端面。由三角关系可以求出光线在光纤中通过的总路程为s=2L/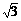，因此该激光在光导纤维中传输所经历的时间是t=s/v=2.7×10^-8s。

2．全反射现象

(1)现象：光从光密介质进入到光速介质中时，随着入射角的增加，折射光线远离法线，强度越来越弱，但是反射光线在远离法线的同时强度越来越强，当折射角达到90度时，折射光线认为全部消失，只剩下反射光线--全反射。

(2)条件：①光从光密介质射向光疏介质；② 入射角达到临界角，即

(3)临界角: 折射角为90⁰(发生全发射)时对应的入射角,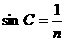

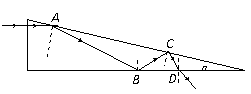[例5] 直角三棱镜的顶角α=15°， 棱镜材料的折射率n=1.5，一细束单色光如图所示垂直于左侧面射入，试用作图法求出该入射光第一次从棱镜中射出的光线。

解：由n=1.5知临界角大于30°小于45°，边画边算可知该光线在射到A、B、C、D各点时的入射角依次是75°、60°、45°、30°，因此在A、B、C均发生全反射，到D点入射角才第一次小于临界角，所以才第一次有光线从棱镜射出。

1．折射定律 (荷兰　 斯涅尔)

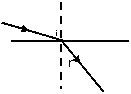光射到两种介质的界面上后从第一种介质进入第二种介质时，其传播规律遵循折射定律．折射定律的基本内容包含如下三个要点：

① 折射光线、法线、入射光线共面；

② 折射光线与入射光线分居法线两侧；

③ 入射角的正弦与折射角的正弦之比等于常数，即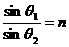

折射定律的各种表达形式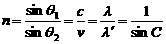： (θ₁为入、折射角中的较大者，C为全反射时的临界角。)

④折射光路是可逆的。

⑤n＞1

⑥介质确定，n确定。(空气1.00028 　水n＝1.33　 酒精n＝1.6)(不以密度为标准)

⑦光密介质和光疏介质--(1)与密度不同(2)相对性 (3)n大角小，n小角大

5．利用边缘光线作图确定范围

[例3] 如图所示，画出人眼在S处通过平面镜可看到障碍物后地面的范围。

解：先根据对称性作出人眼的像点S^/，再根据光路可逆，设想S处有一个点光源，它能通过平面镜照亮的范围就是人眼能通过平面镜看到的范围。图中画出了两条边缘光线。

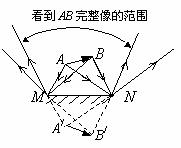
[例4]如图所示，用作图法确定人在镜前通过平面镜可看到AB完整像的范围。

解：先根据对称性作出AB的像A^/B^/，分别作出A点、B点发出的光经平面镜反射后能射到的范围，再找到它们的公共区域(交集)。就是能看到完整像的范围。

4．充分利用光路可逆--在平面镜的计算和作图中要充分利用光路可逆。(眼睛在某点A通过平面镜所能看到的范围和在A点放一个点光源，该点光源发出的光经平面镜反射后照亮的范围是完全相同的。)

3．光路图作法--根据成像的特点，在作光路图时，可以先画像，后补画光路图。

2．平面镜成像的特点--平面镜成的像是正立等大的虚像，像与物关于镜面对称

1、反射定律

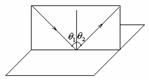光射到两种介质的界面上后返回原介质时，其传播规律遵循反射定律．反射定律的基本内容包含如下三个要点：

① 反射光线、法线、入射光线共面；

② 反射光线与入射光线分居法线两侧；

③ 反射角等于入射角，即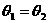　

2．光在同一种均匀介质中是沿直线传播的

注意前提条件：在同一种介质中，而且是均匀介质。否则，可能发生偏折。如光从空气斜射入水中(不是同一种介质)；“海市蜃楼”现象(介质不均匀)。

点评：光的直线传播是一个近似的规律。当障碍物或孔的尺寸和波长可以比拟或者比波长小时，将发生明显的衍射现象，光线将可能偏离原来的传播方向。

[例1]如图所示，在A点有一个小球，紧靠小球的左方有一个点光源S。现将小球从A点正对着竖直墙平抛出去，打到竖直墙之前，小球在点光源照射下的影子在墙上的运动是

A.匀速直线运动　　　 　　　B.自由落体运动

C.变加速直线运动　　 　　　D.匀减速直线运动

解：小球抛出后做平抛运动，时间t后水平位移是vt，竖直位移是h=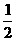gt²，根据相似形知识可以由比例求得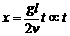，因此影子在墙上的运动是匀速运动。

[例2]某人身高1.8 m，沿一直线以2 m/s的速度前进，其正前方离地面5 m高处有一盏路灯，试求人的影子在水平地面上的移动速度。

解析：如图所示，设人在时间t内由开始位置运动到G位置，人头部的影子由D点运动到C点。

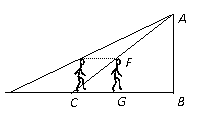三角形ABC∽FGC，有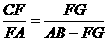

因为三角形ACD∽AFE，所以有

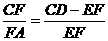
由以上各式可以得到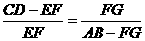

即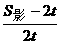=　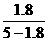 解得S_影=3.125t　 。

可见影的速度为3.125m/s 。