
题目列表(包括答案和解析)
1.质量为m的物体,在距地面h高处以g/3 的加速度由静止竖直下落到地面.下列说法中正确的是B
A.物体的重力势能减少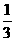 mgh B.物体的动能增加
mgh B.物体的动能增加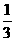 mgh
mgh
C.物体的机械能减少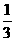 mgh
D.重力做功
mgh
D.重力做功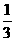 mgh[
mgh[
4.利用动能定理巧求机车脱钩问题
[例9]总质量为M的列车,沿水平直线轨道匀速前进,其末节车厢质量为m,中途脱节,司机发觉时,机车已行驶L的距离,于是立即关闭油门,除去牵引力。设运动的阻力与质量成正比,机车的牵引力是恒定的。当列车的两部分都停止时,它们的距离是多少?
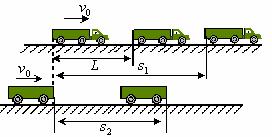 解:对车头,脱钩后的全过程用动能定理得:
解:对车头,脱钩后的全过程用动能定理得:
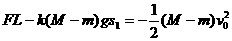 对车尾,脱钩后用动能定理得:
对车尾,脱钩后用动能定理得:
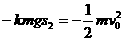
而 ,由于原来列车匀速,所以F=kMg,以上方程解得
,由于原来列车匀速,所以F=kMg,以上方程解得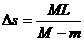 。
。
3.利用动能定理巧求动摩擦因数
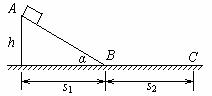
[例8] 如图所示,小滑块从斜面顶点A由静止滑至水平部分C点而停止。已知斜面高为h,滑块运动的整个水平距离为s,设转角B处无动能损失,斜面和水平部分与小滑块的动摩擦因数相同,求此动摩擦因数。
解析:滑块从A点滑到C点,只有重力和摩擦力做功,设滑块质量为m,动摩擦因数为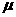 ,斜面倾角为
,斜面倾角为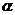 ,斜面底边长s1,水平部分长s2,由动能定理得:
,斜面底边长s1,水平部分长s2,由动能定理得:
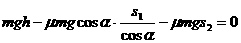
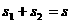 由以上两式得
由以上两式得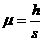
从计算结果可以看出,只要测出斜面高和水平部分长度,即可计算出动摩擦因数。
2.应用动能定理简解多过程问题。
物体在某个运动过程中包含有几个运动性质不同的过程(如加速、减速的过程),此时可以分段考虑,也可以对全过程考虑。
 [例7]
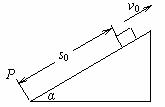
如图所示,斜面足够长,其倾角为α,质量为m的滑块,距挡板P为s0,以初速度v0沿斜面上滑,滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于滑块沿斜面方向的重力分力,若滑块每次与挡板相碰均无机械能损失,求滑块在斜面上经过的总路程为多少?
[例7]
如图所示,斜面足够长,其倾角为α,质量为m的滑块,距挡板P为s0,以初速度v0沿斜面上滑,滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于滑块沿斜面方向的重力分力,若滑块每次与挡板相碰均无机械能损失,求滑块在斜面上经过的总路程为多少?
解析:滑块在滑动过程中,要克服摩擦力做功,其机械能不断减少;又因为滑块所受摩擦力小于滑块沿斜面方向的重力分力,所以最终会停在斜面底端。
在整个过程中,受重力、摩擦力和斜面支持力作用,其中支持力不做功。设其经过和总路程为L,对全过程,由动能定理得:
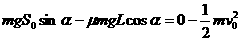 得
得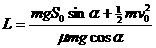
1.应用动能定理巧求变力的功
如果我们所研究的问题中有多个力做功,其中只有一个力是变力,其余的都是恒力,而且这些恒力所做的功比较容易计算,研究对象本身的动能增量也比较容易计算时,用动能定理就可以求出这个变力所做的功。
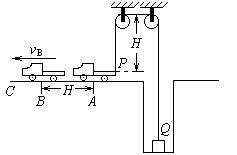 [例5]一辆车通过一根跨过定滑轮的绳PQ提升井中质量为m的物体,如图所示.绳的P端拴在车后的挂钩上,Q端拴在物体上.设绳的总长不变,绳的质量、定滑轮的质量和尺寸、滑轮上的摩擦都忽略不计.开始时,车在A点,左右两侧绳都已绷紧并且是竖直的,左侧绳长为H.提升时,车加速向左运动,沿水平方向从A经过B驶向C.设A到B的距离也为H,车过B点时的速度为vB.求在车由A移到B的过程中,绳Q端的拉力对物体做的功.
[例5]一辆车通过一根跨过定滑轮的绳PQ提升井中质量为m的物体,如图所示.绳的P端拴在车后的挂钩上,Q端拴在物体上.设绳的总长不变,绳的质量、定滑轮的质量和尺寸、滑轮上的摩擦都忽略不计.开始时,车在A点,左右两侧绳都已绷紧并且是竖直的,左侧绳长为H.提升时,车加速向左运动,沿水平方向从A经过B驶向C.设A到B的距离也为H,车过B点时的速度为vB.求在车由A移到B的过程中,绳Q端的拉力对物体做的功.
解析:设绳的P端到达B处时,左边绳与水平地面所成夹角为θ,物体从井底上升的高度为h,速度为v,所求的功为W,则据动能定理可得:
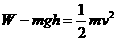 因绳总长不变,所以:
因绳总长不变,所以:
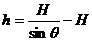
根据绳联物体的速度关系得:v=vBcosθ 由几何关系得: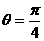
由以上四式求得: 
3.应用动能定理解题的步骤
(1)确定研究对象和研究过程。和动量定理不同,动能定理的研究对象只能是单个物体,如果是系统,那么系统内的物体间不能有相对运动。(原因是:系统内所有内力的总冲量一定是零,而系统内所有内力做的总功不一定是零)。
(2)对研究对象受力分析。(研究对象以外的物体施于研究对象的力都要分析,含重力)。
(3)写出该过程中合外力做的功,或分别写出各个力做的功(注意功的正负)
(4)写出物体的初、末动能。按照动能定理列式求解。
[例2] 将小球以初速度v0竖直上抛,在不计空气阻力的理想状况下,小球将上升到某一最大高度。由于有空气阻力,小球实际上升的最大高度只有该理想高度的80%。设空气阻力大小恒定,求小球落回抛出点时的速度大小v。
解:有空气阻力和无空气阻力两种情况下分别在上升过程对小球用动能定理:
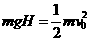 和
和 ,可得H=v02/2g,
,可得H=v02/2g,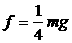
再以小球为对象,在有空气阻力的情况下对上升和下落的全过程用动能定理。全过程重力做的功为零,所以有: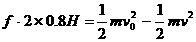 ,解得
,解得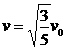
[例3]如图所示,质量为m的钢珠从高出地面h处由静止自由下落,落到地面进入沙坑h/10停止,则
(1)钢珠在沙坑中受到的平均阻力是重力的多少倍?
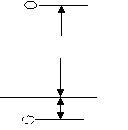 (2)若让钢珠进入沙坑h/8,则钢珠在h处的动能应为多少?设钢珠在沙坑中所受平均阻力大小不随深度改变。
(2)若让钢珠进入沙坑h/8,则钢珠在h处的动能应为多少?设钢珠在沙坑中所受平均阻力大小不随深度改变。
解析:(1)取钢珠为研究对象,对它的整个运动过程,由动能定理得W=WF+WG=△EK =0。取钢珠停止处所在水平面为重力势能的零参考平面,则重力的功WG=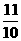 mgh,阻力的功WF=
mgh,阻力的功WF=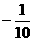 Ff h, 代入得
Ff h, 代入得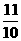 mgh
mgh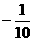 Ff h=0,故有Ff /mg=11。即所求倍数为11。
Ff h=0,故有Ff /mg=11。即所求倍数为11。
(2)设钢珠在h处的动能为EK,则对钢珠的整个运动过程,由动能定理得W=WF+WG=△EK =0,进一步展开为9mgh/8-Ff h/8= -EK,得EK=mgh/4。
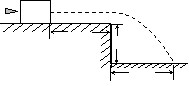 [例4] 质量为M的木块放在水平台面上,台面比水平地面高出h=0.20m,木块离台的右端L=1.7m。质量为m=0.10M的子弹以v0=180m/s的速度水平射向木块,并以v=90m/s的速度水平射出,木块落到水平地面时的落地点到台面右端的水平距离为s=1.6m,求木块与台面间的动摩擦因数为μ。
[例4] 质量为M的木块放在水平台面上,台面比水平地面高出h=0.20m,木块离台的右端L=1.7m。质量为m=0.10M的子弹以v0=180m/s的速度水平射向木块,并以v=90m/s的速度水平射出,木块落到水平地面时的落地点到台面右端的水平距离为s=1.6m,求木块与台面间的动摩擦因数为μ。
解:本题的物理过程可以分为三个阶段,在其中两个阶段中有机械能损失:子弹射穿木块阶段和木块在台面上滑行阶段。所以本题必须分三个阶段列方程:
子弹射穿木块阶段,对系统用动量守恒,设木块末速度为v1,mv0= mv+Mv1……①[
木块在台面上滑行阶段对木块用动能定理,设木块离开台面时的速度为v2,
有: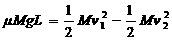 ……②
……②
木块离开台面后平抛阶段,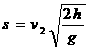 …③
, 由①、②、③可得μ=0.50
…③
, 由①、②、③可得μ=0.50
2.对外力做功与动能变化关系的理解:
外力对物体做正功,物体的动能增加,这一外力有助于物体的运动,是动力;外力对物体做负功,物体的动能减少,这一外力是阻碍物体的运动,是阻力,外力对物体做负功往往又称物体克服阻力做功.
功是能量转化的量度,外力对物体做了多少功;就有多少动能与其它形式的能发生了转化.所以外力对物体所做的功就等于物体动能的变化量.即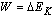 .
.
1. 动能定理的推导
物体只在一个恒力作用下,做直线运动
w=FS=m a ×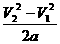 即 w=
即 w=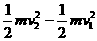
推广: 物体在多个力的作用下、物体在做曲线运动、物体在变力的作用下
结论: 合力所做的功等于动能的增量 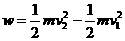 合力做正功动能增加,合力做负功动能减小
合力做正功动能增加,合力做负功动能减小
注:动能定理表达式是一个标量式,不能在某一个方向上应用动能定理。
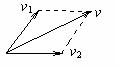 [例1] 一个质量为m的物体静止放在光滑水平面上,在互成60°角的大小相等的两个水平恒力作用下,经过一段时间,物体获得的速度为v,在力的方向上获得的速度分别为v1、v2,那么在这段时间内,其中一个力做的功为
[例1] 一个质量为m的物体静止放在光滑水平面上,在互成60°角的大小相等的两个水平恒力作用下,经过一段时间,物体获得的速度为v,在力的方向上获得的速度分别为v1、v2,那么在这段时间内,其中一个力做的功为
A.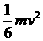 B.
B.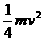 C.
C.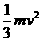 D.
D.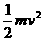
错解:在分力F1的方向上,由动动能定理得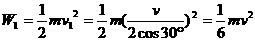 ,故A正确。
,故A正确。
正解:在合力F的方向上,由动动能定理得,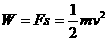 ,某个分力的功为
,某个分力的功为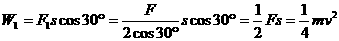 ,故B正确。
,故B正确。
2、弹性势能(Ep) 弹性形变
弹性形变
发生形变的物体,在恢复原状时能够对外做功,因而具有能量,叫弹性势能,跟物体形变和材料有关。
1、重力势能(Ep) 举高。物体由于受到重力的作用,而具有的与其相对位置有关的能量叫做重力势能。 Ep=m g h (h是重心相对于零势能面的高度)[
举高。物体由于受到重力的作用,而具有的与其相对位置有关的能量叫做重力势能。 Ep=m g h (h是重心相对于零势能面的高度)[
(1)、相对性 ①“零高度”或“零势能面”,(大地或最低点)
②势能的正负和大小是相对于零势能面的
③势能的正负和大小于零势能面的选取有关
(2)重力势能变化量的绝对性--
①跟物体的初位置的高度和末位置的高度有 关,跟物体运动的路径无关。
②重力势能改变量与零势能面的选取无关
③重力势能的改变量与路径无关
(3)重力势能的改变--重力做正功,重力势能减 小,重力做负功,重力势能增大(等值变化)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com