
题目列表(包括答案和解析)
6、解题方法指导:
解题步骤:
(1)确定研究对象。(2)明确物体作什么运动,并且画出运动示意图。(3)分析研究对象的运动过程及特点,合理选择公式,注意多个运动过程的联系。(4)确定正方向,列方程求解。(5)对结果进行讨论、验算。
解题方法:
(1)公式解析法:假设未知数,建立方程组。本章公式多,且相互联系,一题常有多种解法。要熟记每个公式的特点及相关物理量。
(2)图象法:如用v-t图可以求出某段时间的位移大小、可以比较vt/2与vS/2,以及追及问题。用s-t图可求出任意时间内的平均速度。
(3)比例法:用已知的讨论,用比例的性质求解。
(4)极值法:用二次函数配方求极值,追赶问题用得多。
(5)逆向思维法:如匀减速直线运动可视为反方向的匀加速直线运动来求解。
综合应用例析
 [例1]在光滑的水平面上静止一物体,现以水平恒力甲推此物体,作用一段时间后换成相反方向的水平恒力乙推物体,当恒力乙作用时间与恒力甲的作用时间相同时,物体恰好回到原处,此时物体的速度为v2,若撤去恒力甲的瞬间物体的速度为v1,则v2∶v1=?
[例1]在光滑的水平面上静止一物体,现以水平恒力甲推此物体,作用一段时间后换成相反方向的水平恒力乙推物体,当恒力乙作用时间与恒力甲的作用时间相同时,物体恰好回到原处,此时物体的速度为v2,若撤去恒力甲的瞬间物体的速度为v1,则v2∶v1=?
[解析]
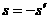 ,而
,而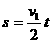 ,
,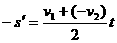 得v2∶v1=2∶1
得v2∶v1=2∶1
思考:在例1中,F1、F2大小之比为多少?(答案:1∶3)
 [例2]一辆汽车沿平直公路从甲站开往乙站,起动加速度为2m/s2,加速行驶5秒,后匀速行驶2分钟,然后刹车,滑行50m,正好到达乙站,求汽车从甲站到乙站的平均速度?
[例2]一辆汽车沿平直公路从甲站开往乙站,起动加速度为2m/s2,加速行驶5秒,后匀速行驶2分钟,然后刹车,滑行50m,正好到达乙站,求汽车从甲站到乙站的平均速度?
解析:起动阶段行驶位移为:
s1=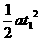 ……(1)
……(1)
匀速行驶的速度为: v= at1 ……(2)
匀速行驶的位移为: s2 =vt2 ……(3)
刹车段的时间为: s3 =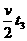 ……(4)
……(4)
汽车从甲站到乙站的平均速度为:
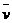 =
=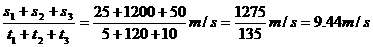
[例3]一物体由斜面顶端由静止开始匀加速下滑,最初的3秒内的位移为s1,最后3秒内的位移为s2,若s2-s1=6米,s1∶s2=3∶7,求斜面的长度为多少?
解析:设斜面长为s,加速度为a,沿斜面下滑的总时间为t 。则:
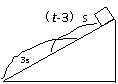 斜面长: s =
斜面长: s = 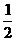 at2 …… ( 1)
at2 …… ( 1)
前3秒内的位移:s1
= 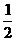 at12 ……(2)
at12 ……(2)
后3秒内的位移:
s2 =s -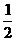 a (t-3)2 …… (3)
a (t-3)2 …… (3)
s2-s1=6 …… (4) s1∶s2 = 3∶7 …… (5)
解(1)-(5)得:a=1m/s2 t= 5s s=12 . 5m
 [例4]物块以v0=4米/秒的速度滑上光滑的斜面,途经A、B两点,已知在A点时的速度是B点时的速度的2倍,由B点再经0.5秒物块滑到斜面顶点C速度变为零,A、B相距0.75米,求斜面的长度及物体由D运动到B的时间?
[例4]物块以v0=4米/秒的速度滑上光滑的斜面,途经A、B两点,已知在A点时的速度是B点时的速度的2倍,由B点再经0.5秒物块滑到斜面顶点C速度变为零,A、B相距0.75米,求斜面的长度及物体由D运动到B的时间?
解析:物块匀减速直线运动。设A点速度为VA、B点速度VB,加速度为a,斜面长为S。
A到B: vB2 - vA2 =2asAB ……(1)
vA = 2vB … …(2)
B到C: 0=vB + at0 ……..(3)
解(1)(2)(3)得:vB=1m/s a= -2m/s2
D到C 0 - v02=2as (4) s= 4m
从D运动到B的时间: D到B: vB =v0+ at1 t1=1.5秒
D到C再回到B:t2 = t1+2t0=1.5+2´0.5=2.5(s)
[例5]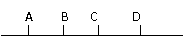 一质点沿AD直线作匀加速直线运动,如图,测得它在AB、BC、CD三段的时间均为t,测得位移AC=L1,BD=L2,试求质点的加速度?
一质点沿AD直线作匀加速直线运动,如图,测得它在AB、BC、CD三段的时间均为t,测得位移AC=L1,BD=L2,试求质点的加速度?
解:设AB=s1、BC=s2、CD=s3 则:
s2-s1=at2 s3-s2=at2
两式相加:s3-s1=2at2
由图可知:L2-L1=(s3+s2)-(s2+s1)=s3-s1
则:a = 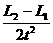
[例6]一质点由A点出发沿直线AB运动,行程的第一部分是加速度为a1的匀加速运动,接着做加速度为a2的匀减速直线运动,抵达B点时恰好静止,如果AB的总长度为s,试求质点走完AB全程所用的时间t?
解:设质点的最大速度为v,前、后两段运动过程及全过程的平均速度相等,均为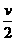 。
。
全过程: s=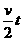 ……(1)
……(1)
匀加速过程:v = a1t1 ……(2) 匀减速过程:v = a2t2 ……(3)
由(2)(3)得:t1=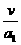
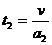 代入(1)得:
代入(1)得:
s = 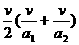 s=
s=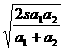
将v代入(1)得: t = 
[例7]一个做匀加速直线运动的物体,连续通过两段长为s的位移所用的时间分别为t1、t2,求物体的加速度?
解:方法(1):设前段位移的初速度为v0,加速度为a,则:
前一段s: s=v0t1
+ 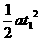 ……(1)
……(1)
全过程2s: 2s=v0(t1+t2)+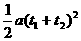 ……(2)
……(2)
消去v0得: a = 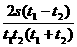
方法(2):设前一段时间t1的中间时刻的瞬时速度为v1,后一段时间t2的中间时刻的瞬时速度为v2。所以:
v1=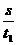 ……(1) v2=
……(1) v2=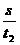 ……(2)v2=v1+a(
……(2)v2=v1+a(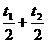 ) ……(3)
) ……(3)
解(1)(2)(3)得相同结果。
方法(3):设前一段位移的初速度为v0,末速度为v,加速度为a。
前一段s: s=v0t1
+ 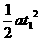 ……(1)
……(1)
后一段s: s=vt2 +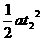 ……(2) v = v0 + at ……(3)
……(2) v = v0 + at ……(3)
解(1)(2)(3)得相同结果。
例8.某航空公司的一架客机,在正常航线上做水平飞行时,突然受到强大的垂直气流的作用,使飞机在10 s内下降高度为1800 m,造成众多乘客和机组人员的伤害事故,如果只研究在竖直方向上的运动,且假设这一运动是匀变速直线运动.
(1)求飞机在竖直方向上产生的加速度多大?
(2)试估算成年乘客所系安全带必须提供多大拉力才能使乘客不脱离座椅.
解:由s=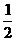 at2及:a=
at2及:a=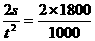 m/s2=36 m/s2.
m/s2=36 m/s2.
由牛顿第二定律:F+mg=ma得F=m(a-g)=1560 N,成年乘客的质量可取45 kg~65 kg,因此,F相应的值为1170 N~1690 N
5.一种典型的运动
经常会遇到这样的问题:物体由静止开始先做匀加速直线运动,紧接着又做匀减速直线运动到静止。用右图描述该过程,可以得出以下结论:
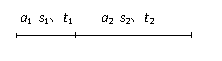 ①
①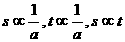 ②
②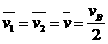
4.初速为零的匀变速直线运动
①前1秒、前2秒、前3秒……内的位移之比为1∶4∶9∶……
②第1秒、第2秒、第3秒……内的位移之比为1∶3∶5∶……
③前1米、前2米、前3米……所用的时间之比为1∶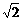 ∶
∶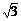 ∶……
∶……
④第1米、第2米、第3米……所用的时间之比为1∶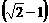 ∶(
∶(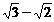 )∶……
)∶……
对末速为零的匀变速直线运动,可以相应的运用这些规律。
3.初速度为零(或末速度为零)的匀变速直线运动
做匀变速直线运动的物体,如果初速度为零,或者末速度为零,那么公式都可简化为:
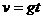 ,
, 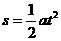 ,
, 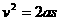 ,
, 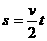
2.匀变速直线运动中几个常用的结论
①Δs=aT 2,即任意相邻相等时间内的位移之差相等。可以推广到sm-sn=(m-n)aT 2
②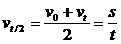 ,某段时间的中间时刻的即时速度等于该段时间内的平均速度。
,某段时间的中间时刻的即时速度等于该段时间内的平均速度。
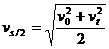 ,某段位移的中间位置的即时速度公式(不等于该段位移内的平均速度)。
,某段位移的中间位置的即时速度公式(不等于该段位移内的平均速度)。
可以证明,无论匀加速还是匀减速,都有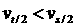 。
。
1.常用公式有以下四个
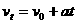
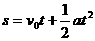
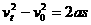
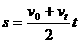
5.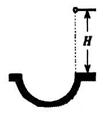 如图所示,质量m=0.5kg的小球从距地面高H=5m处自由下落,到达地面恰能沿凹陷于地面的半圆形槽壁运动,半圆槽半径R=0.4m。小球到达槽最低点时速率为10m/s,并继续沿槽壁运动直到从槽右端边缘飞出……,如此反复几次,设摩擦力恒定不变,求:(设小球与槽壁相碰时不损失能量)
如图所示,质量m=0.5kg的小球从距地面高H=5m处自由下落,到达地面恰能沿凹陷于地面的半圆形槽壁运动,半圆槽半径R=0.4m。小球到达槽最低点时速率为10m/s,并继续沿槽壁运动直到从槽右端边缘飞出……,如此反复几次,设摩擦力恒定不变,求:(设小球与槽壁相碰时不损失能量)
(1)小球第一次离槽上升的高度h;
(2)小球最多能飞出槽外的次数(取g=10m/s2)。
解析:(1)小球落至槽底部的整个过程中,由动能定理得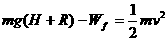 得
得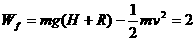 J
J
由对称性知小球从槽底到槽左端口摩擦力的功也为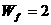 J,则小球第一次离槽上升的高度h,由
J,则小球第一次离槽上升的高度h,由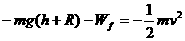 得
得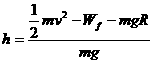 =4.2m
=4.2m
(2)设小球飞出槽外n次,则由动能定理得
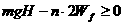 ∴
∴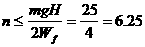
即小球最多能飞出槽外6次。
4.质量为m的飞机以水平速度v0飞离跑道后逐渐上升,若飞机在此过程中水平速度保持不变,同时受到重力和竖直向上的恒定升力(该升力由其他力的合力提供,不含重力),今测得当飞机在水平方向的位移为l时,它的上升高度为h,求:(1)飞机受到的升力大小;(2)从起飞到上升至h高度的过程中升力所做的功及在高度h处飞机的动能.
解析:(1)飞机水平速度不变
l=v0t y方向加速度恒定 h=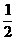 at2 即得a=
at2 即得a=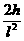
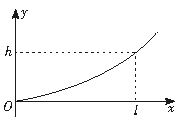 由牛顿第二定律 F=mg+ma=mg(1+
由牛顿第二定律 F=mg+ma=mg(1+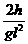 v02)
v02)
(2)升力做功W=Fh=mgh(1+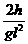 v02) [
v02) [
在h处vt=at=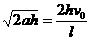
Ek=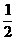 m(v02+vt2)
=
m(v02+vt2)
=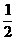 mv02(1+
mv02(1+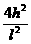 )
)
3. 如图所示,木板长为l,板的A端放一质量为m的小物块,物块与板间的动摩擦因数为μ。开始时板水平,在绕O点缓慢转过一个小角度θ的过程中,若物块始终保持与板相对静止。对于这个过程中各力做功的情况,下列说法正确的是 ( C )
如图所示,木板长为l,板的A端放一质量为m的小物块,物块与板间的动摩擦因数为μ。开始时板水平,在绕O点缓慢转过一个小角度θ的过程中,若物块始终保持与板相对静止。对于这个过程中各力做功的情况,下列说法正确的是 ( C )
A、摩擦力对物块所做的功为mglsinθ(1-cosθ)
B、弹力对物块所做的功为mglsinθcosθ
C、木板对物块所做的功为mglsinθ
D、合力对物块所做的功为mgl cosθ
2.质量为m的小球用长度为L的轻绳系住,在竖直平面内做圆周运动,运动过程中小球受空气阻力作用.已知小球经过最低点时轻绳受的拉力为7mg,经过半周小球恰好能通过最高点,则此过程中小球克服空气阻力做的功为C
A.mgL/4 B.mgL/3 C.mgL/2 D.mgL
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com