
题目列表(包括答案和解析)
2.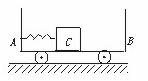 小车AB静置于光滑的水平面上,A端固定一个轻质弹簧,B端粘有橡皮泥,AB车质量为M,长为L,质量为m的木块C放在小车上,用细绳连结于小车的A端并使弹簧压缩,开始时AB与C都处于静止状态,如图所示,当突然烧断细绳,弹簧被释放,使物体C离开弹簧向B端冲去,并跟B端橡皮泥粘在一起,以下说法中正确的是 BCD
小车AB静置于光滑的水平面上,A端固定一个轻质弹簧,B端粘有橡皮泥,AB车质量为M,长为L,质量为m的木块C放在小车上,用细绳连结于小车的A端并使弹簧压缩,开始时AB与C都处于静止状态,如图所示,当突然烧断细绳,弹簧被释放,使物体C离开弹簧向B端冲去,并跟B端橡皮泥粘在一起,以下说法中正确的是 BCD
A.如果AB车内表面光滑,整个系统任何时刻机械能都守恒]
B.整个系统任何时刻动量都守恒
C.当木块对地运动速度为v时,小车对地运动速度为 v
v
 D.AB车向左运动最大位移小于
D.AB车向左运动最大位移小于 L[
L[
1.质量相同的两个小球在光滑水平面上沿连心线同向运动,球1的动量为 7 kg·m/s,球2的动量为5 kg·m/s,当球1追上球2时发生碰撞,则碰撞后两球动量变化的可能值是A
A.Δp1=-1 kg·m/s,Δp2=1 kg·m/s
B.Δp1=-1 kg·m/s,Δp2=4 kg·m/s
C.Δp1=-9 kg·m/s,Δp2=9 kg·m/s
D.Δp1=-12 kg·m/s,Δp2=10 kg·m/s[
3.如图所示,在沙堆表面放置一长方形木块A,其上面再放一个质量为m=0.10kg的爆竹B,木块的质量为M=6.0kg。当爆竹爆炸时,因反冲作用使木块陷入沙中深度h=50cm,而木块所受的平均阻力为f=80N。若爆竹的火药质量以及空气阻力可忽略不计,g取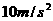 ,求爆竹能上升的最大高度。
,求爆竹能上升的最大高度。
解:爆竹爆炸瞬间,木块获得的瞬时速度v可由牛顿第二定律和运动学公式求得

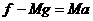 ,
,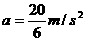 ,
,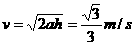
爆竹爆炸过程中,爆竹木块系统动量守恒  [来源:Z。xx。]
[来源:Z。xx。]
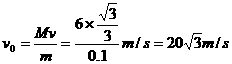
练习2
2.如图所示,放在光滑水平桌面上的A、B木块中部夹一被压缩的弹簧,当弹簧被放开时,它们各自在桌面上滑行一段距离后,飞离桌面落在地上。A的落地点与桌边水平距离0.5m,B的落地点距离桌边1m,那么( A、B、D)
A.A、B离开弹簧时的速度比为1∶2
B.A、B质量比为2∶1
C.未离开弹簧时,A、B所受冲量比为1∶2
D.未离开弹簧时,A、B加速度之比1∶2
练习1
1.质量为M的小车在水平地面上以速度v0匀速向右运动。当车中的砂子从底部的漏斗中不断流下时,车子速度将( B )
A.减小
B.不变 C.增大 D.无法确定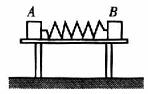
6.物块与平板间的相对滑动
[例8]如图所示,一质量为M的平板车B放在光滑水平面上,在其右端放一质量为m的小木块A,m<M,A、B间动摩擦因数为μ,现给A和B以大小相等、方向相反的初速度v0,使A开始向左运动,B开始向右运动,最后A不会滑离B,求:
(1)A、B最后的速度大小和方向;
(2)从地面上看,小木块向左运动到离出发点最远处时,平板车向右运动位移大小。
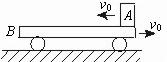 解析:(1)由A、B系统动量守恒定律得:
解析:(1)由A、B系统动量守恒定律得:
Mv0-mv0=(M+m)v ①
所以v=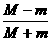 v0 方向向右
v0 方向向右
 (2)A向左运动速度减为零时,到达最远处,此时板车移动位移为s,速度为v′,则由动量守恒定律得:Mv0-mv0=Mv′ ①
(2)A向左运动速度减为零时,到达最远处,此时板车移动位移为s,速度为v′,则由动量守恒定律得:Mv0-mv0=Mv′ ①
对板车应用动能定理得:
-μmgs=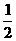 mv′2-
mv′2-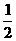 mv02
②[
mv02
②[
联立①②解得:s=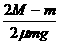 v02
v02
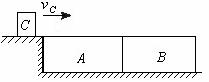
[例9]两块厚度相同的木块A和B,紧靠着放在光滑的水平面上,其质量分别为 ,
,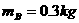 ,它们的下底面光滑,上表面粗糙;另有一质量
,它们的下底面光滑,上表面粗糙;另有一质量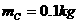 的滑块C(可视为质点),以
的滑块C(可视为质点),以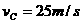 的速度恰好水平地滑到A的上表面,如图所示,由于摩擦,滑块最后停在木块B上,B和C的共同速度为3.0m/s,求:
的速度恰好水平地滑到A的上表面,如图所示,由于摩擦,滑块最后停在木块B上,B和C的共同速度为3.0m/s,求:
(1)木块A的最终速度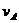 ;
(2)滑块C离开A时的速度
;
(2)滑块C离开A时的速度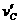 。
。
解析:这是一个由A、B、C三个物体组成的系统,以这系统为研究对象,当C在A、B上滑动时,A、B、C三个物体间存在相互作用,但在水平方向不存在其他外力作用,因此系统的动量守恒。
(1)当C滑上A后,由于有摩擦力作用,将带动A和B一起运动,直至C滑上B后,A、B两木块分离,分离时木块A的速度为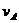 。最后C相对静止在B上,与B以共同速度
。最后C相对静止在B上,与B以共同速度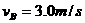 运动,由动量守恒定律有
运动,由动量守恒定律有 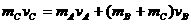
∴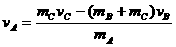 =
=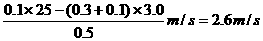
(2)为计算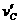 ,我们以B、C为系统,C滑上B后与A分离,C、B系统水平方向动量守恒。C离开A时的速度为
,我们以B、C为系统,C滑上B后与A分离,C、B系统水平方向动量守恒。C离开A时的速度为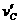 , B与A的速度同为
, B与A的速度同为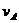 ,由动量守恒定律有
,由动量守恒定律有
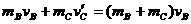
∴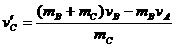
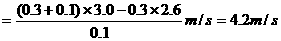
5.某一方向上的动量守恒
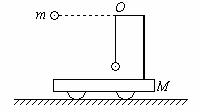
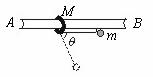
[例7] 如图所示,AB为一光滑水平横杆,杆上套一质量为M的小圆环,环上系一长为L质量不计的细绳,绳的另一端拴一质量为m的小球,现将绳拉直,且与AB平行,由静止释放小球,则当线绳与A B成θ角时,圆环移动的距离是多少?
解析:虽然小球、细绳及圆环在运动过程中合外力不为零(杆的支持力与两圆环及小球的重力之和不相等)系统动量不守恒,但是系统在水平方向不受外力,因而水平动量守恒。设细绳与AB成θ角时小球的水平速度为v,圆环的水平速度为V,则由水平动量守恒有:MV=mv
且在任意时刻或位置V与v均满足这一关系,加之时间相同,公式中的V和v可分别用其水平位移替代,则上式可写为:
Md=m[(L-Lcosθ)-d]
解得圆环移动的距离: d=mL(1-cosθ)/(M+m)[
4.爆炸类问题
[例6] 抛出的手雷在最高点时水平速度为10m/s,这时突然炸成两块,其中大块质量300g仍按原方向飞行,其速度测得为50m/s,另一小块质量为200g,求它的速度的大小和方向。
分析:手雷在空中爆炸时所受合外力应是它受到的重力G=( m1+m2 )g,可见系统的动量并不守恒。但在爆炸瞬间,内力远大于外力时,外力可以不计,系统动量近似守恒。
设手雷原飞行方向为正方向,则整体初速度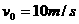 ;m1=0.3kg的大块速度为
;m1=0.3kg的大块速度为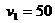 m/s、m2=0.2kg的小块速度为
m/s、m2=0.2kg的小块速度为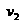 ,方向不清,暂设为正方向。
,方向不清,暂设为正方向。
由动量守恒定律: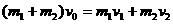
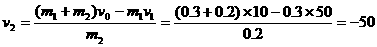 m/s
m/s
 此结果表明,质量为200克的部分以50m/s的速度向反方向运动,其中负号表示与所设正方向相反
此结果表明,质量为200克的部分以50m/s的速度向反方向运动,其中负号表示与所设正方向相反
3.反冲问题
在某些情况下,原来系统内物体具有相同的速度,发生相互作用后各部分的末速度不再相同而分开。这类问题相互作用过程中系统的动能增大,有其它能向动能转化。可以把这类问题统称为反冲。
[例4] 质量为m的人站在质量为M,长为L的静止小船的右端,小船的左端靠在岸边。当他向左走到船的左端时,船左端离岸多远?
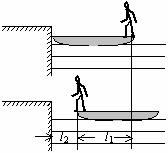 解析:先画出示意图。人、船系统动量守恒,总动量始终为零,所以人、船动量大小始终相等。从图中可以看出,人、船的位移大小之和等于L。设人、船位移大小分别为l1、l2,则:
解析:先画出示意图。人、船系统动量守恒,总动量始终为零,所以人、船动量大小始终相等。从图中可以看出,人、船的位移大小之和等于L。设人、船位移大小分别为l1、l2,则:
mv1=Mv2,两边同乘时间t,ml1=Ml2,而l1+l2=L,
∴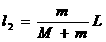
点评:应该注意到:此结论与人在船上行走的速度大小无关。不论是匀速行走还是变速行走,甚至往返行走,只要人最终到达船的左端,那么结论都是相同的。
以上列举的人、船模型的前提是系统初动量为零。如果发生相互作用前系统就具有一定的动量,就不能再用m1v1=m2v2这种形式列方程,而要用(m1+m2)v0= m1v1+ m2v2列式。
[例5] 总质量为M的火箭模型 从飞机上释放时的速度为v0,速度方向水平。火箭向后以相对于地面的速率u喷出质量为m的燃气后,火箭本身的速度变为多大?
解析:火箭喷出燃气前后系统动量守恒。喷出燃气后火箭剩余质量变为M-m,以v0方向为正方向,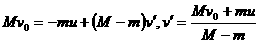
2.子弹打木块类问题
 子弹打木块实际上是一种完全非弹性碰撞。作为一个典型,它的特点是:子弹以水平速度射向原来静止的木块,并留在木块中跟木块共同运动。下面从动量、能量和牛顿运动定律等多个角度来分析这一过程。
子弹打木块实际上是一种完全非弹性碰撞。作为一个典型,它的特点是:子弹以水平速度射向原来静止的木块,并留在木块中跟木块共同运动。下面从动量、能量和牛顿运动定律等多个角度来分析这一过程。
[例3] 设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块,并留在木块中不再射出,子弹钻入木块深度为d。求木块对子弹的平均阻力的大小和该过程中木块前进的距离。
解析:子弹和木块最后共同运动,相当于完全非弹性碰撞。
从动量的角度看,子弹射入木块过程中系统动量守恒: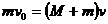
从能量的角度看,该过程系统损失的动能全部转化为系统的内能。设平均阻力大小为f,设子弹、木块的位移大小分别为s1、s2,如图所示,显然有s1-s2=d
对子弹用动能定理: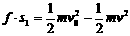 ……①
……①
对木块用动能定理: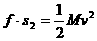 ……②
……②
①、②相减得: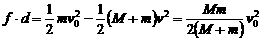 ……③
……③
点评:这个式子的物理意义是:fžd恰好等于系统动能的损失;根据能量守恒定律,系统动能的损失应该等于系统内能的增加;可见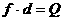 ,即两物体由于相对运动而摩擦产生的热(机械能转化为内能),等于摩擦力大小与两物体相对滑动的路程的乘积(由于摩擦力是耗散力,摩擦生热跟路径有关,所以这里应该用路程,而不是用位移)。
,即两物体由于相对运动而摩擦产生的热(机械能转化为内能),等于摩擦力大小与两物体相对滑动的路程的乘积(由于摩擦力是耗散力,摩擦生热跟路径有关,所以这里应该用路程,而不是用位移)。
由上式不难求得平均阻力的大小: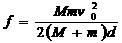
至于木块前进的距离s2,可以由以上②、③相比得出: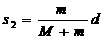
从牛顿运动定律和运动学公式出发,也可以得出同样的结论。由于子弹和木块都在恒力作用下做匀变速运动,位移与平均速度成正比:
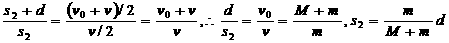
一般情况下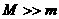 ,所以s2<<d。这说明,在子弹射入木块过程中,木块的位移很小,可以忽略不计。这就为分阶段处理问题提供了依据。象这种运动物体与静止物体相互作用,动量守恒,最后共同运动的类型,全过程动能的损失量可用公式:
,所以s2<<d。这说明,在子弹射入木块过程中,木块的位移很小,可以忽略不计。这就为分阶段处理问题提供了依据。象这种运动物体与静止物体相互作用,动量守恒,最后共同运动的类型,全过程动能的损失量可用公式: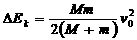 …④
…④
当子弹速度很大时,可能射穿木块,这时末状态子弹和木块的速度大小不再相等,但穿透过程中系统动量仍然守恒,系统动能损失仍然是ΔEK= f žd(这里的d为木块的厚度),但由于末状态子弹和木块速度不相等,所以不能再用④式计算ΔEK的大小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com