
题目列表(包括答案和解析)
1.将一球竖直上抛,若该球所受的空气阻力大小不变,则其力大小不变,则其上升和下降两过程的时间及损失的机械能的关系是( C )
A.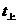 >
>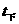 ,
,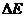
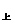 >
>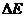
 B.
B.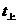 <
<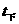 ,
,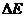
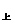 <
<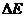

C.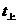 <
<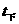 ,
,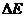
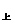 =
=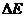
 D.
D.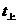 =
=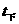 ,
,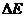
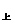 =
=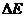

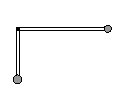 例1、如图所示,质量分别为2 m和3m的两个小球固定在一根直角尺的两端A、B,直角尺的顶点O处有光滑的固定转动轴。AO、BO的长分别为2L和L。开始时直角尺的AO部分处于水平位置而B在O的正下方。让该系统由静止开始自由转动,求:⑴当A到达最低点时,A小球的速度大小v;⑵ B球能上升的最大高度h;⑶开始转动后B球可能达到的最大速度vm。
例1、如图所示,质量分别为2 m和3m的两个小球固定在一根直角尺的两端A、B,直角尺的顶点O处有光滑的固定转动轴。AO、BO的长分别为2L和L。开始时直角尺的AO部分处于水平位置而B在O的正下方。让该系统由静止开始自由转动,求:⑴当A到达最低点时,A小球的速度大小v;⑵ B球能上升的最大高度h;⑶开始转动后B球可能达到的最大速度vm。
解析:以直角尺和两小球组成的系统为对象,由于转动过程不受摩擦和介质阻力,所以该系统的机械能守恒。
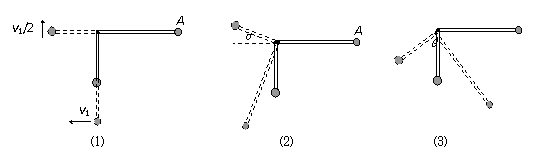
⑴过程中A的重力势能减少, A、B的动能和B的重力势能增加,A的即时速度总是B的2倍。
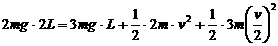 ,解得
,解得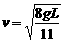
⑵B球不可能到达O的正上方,它到达最大高度时速度一定为零,设该位置比OA竖直位置向左偏了α角。2mgž2Lcosα=3mgžL(1+sinα),此式可化简为4cosα-3sinα=3,解得sin(53°-α)=sin37°,α=16°
⑶B球速度最大时就是系统动能最大时,而系统动能增大等于系统重力做的功WG。设OA从开始转过θ角时B球速度最大,
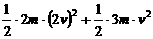 =2mgž2Lsinθ-3mgžL(1-cosθ)
=2mgž2Lsinθ-3mgžL(1-cosθ)
=mgL(4sinθ+3cosθ-3)≤2mgžL,解得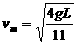
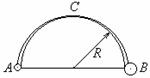 例2、如图所示,半径为
例2、如图所示,半径为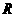 的光滑半圆上有两个小球
的光滑半圆上有两个小球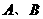 ,质量分别为
,质量分别为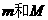 ,由细线挂着,今由静止开始无初速度自由释放,求小球
,由细线挂着,今由静止开始无初速度自由释放,求小球 升至最高点
升至最高点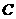 时
时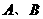 两球的速度?
两球的速度?
解析: 球沿半圆弧运动,绳长不变,
球沿半圆弧运动,绳长不变,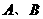 两球通过的路程相等,
两球通过的路程相等, 上升的高度为
上升的高度为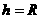 ;
;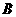 球下降的高度为
球下降的高度为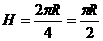 ;对于系统,由机械能守恒定律得:
;对于系统,由机械能守恒定律得: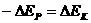 ;
;
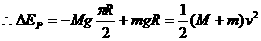
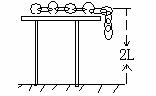
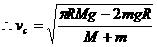
例3、如图所示,均匀铁链长为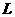 ,平放在距离地面高为
,平放在距离地面高为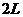 的光滑水平面上,其长度的
的光滑水平面上,其长度的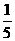 悬垂于桌面下,从静止开始释放铁链,求铁链下端刚要着地时的速度?
悬垂于桌面下,从静止开始释放铁链,求铁链下端刚要着地时的速度?
解:选取地面为零势能面: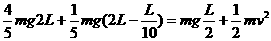 得:
得: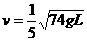
 例4、如图所示,粗细均匀的U形管内装有总长为4L的水。开始时阀门K闭合,左右支管内水面高度差为L。打开阀门K后,左右水面刚好相平时左管液面的速度是多大?(管的内部横截面很小,摩擦忽略不计)
例4、如图所示,粗细均匀的U形管内装有总长为4L的水。开始时阀门K闭合,左右支管内水面高度差为L。打开阀门K后,左右水面刚好相平时左管液面的速度是多大?(管的内部横截面很小,摩擦忽略不计)
解析:由于不考虑摩擦阻力,故整个水柱的机械能守恒。从初始状态到左右支管水面相平为止,相当于有长L/2的水柱由左管移到右管。系统的重力势能减少,动能增加。该过程中,整个水柱势能的减少量等效于高L/2的水柱降低L/2重力势能的减少。不妨设水柱总质量为8m,则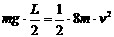 ,得
,得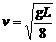 。
。
点评:需要注意的是研究对象仍然是整个水柱,到两个支管水面相平时,整个水柱中的每一小部分的速率都是相同的。
例5、如图所示,游乐列车由许多节车厢组成。列车全长为L,圆形轨道半径为R,(R远大于一节车厢的高度h和长度l,但L>2πR).已知列车的车轮是卡在导轨上的光滑槽中只能使列车沿着圆周运动,在轨道的任何地方都不能脱轨。试问:在没有任何动力的情况下,列车在水平轨道上应具有多大初速度v0,才能使列车通过圆形轨道而运动到右边的水平轨道上?
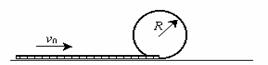 解析:当游乐车灌满整个圆形轨道时,游乐车的速度最小,设此时速度为v,游乐车的质量为m,则据机械能守恒定律得:
解析:当游乐车灌满整个圆形轨道时,游乐车的速度最小,设此时速度为v,游乐车的质量为m,则据机械能守恒定律得: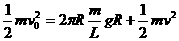
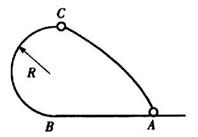 要游乐车能通过圆形轨道,则必有v>0,所以有
要游乐车能通过圆形轨道,则必有v>0,所以有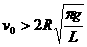
例6、小球在外力作用下,由静止开始从A点出发做匀加速直线运动,到B点时消除外力。然后,小球冲上竖直平面内半径为R的光滑半圆环,恰能维持在圆环上做圆周运动,到达最高点C后抛出,最后落回到原来的出发点A处,如图所示,试求小球在AB段运动的加速度为多大?
解析:要题的物理过程可分三段:从A到孤匀加速直线运动过程;从B沿圆环运动到C的圆周运动,且注意恰能维持在圆环上做圆周运动,在最高点满足重力全部用来提供向心力;从C回到A的平抛运动。
根据题意,在C点时,满足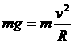 ①
①
从B到C过程,由机械能守恒定律得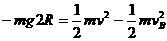 ②
②
由①、②式得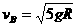 从C回到A过程,满足
从C回到A过程,满足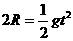 ③
③
水平位移s=vt,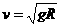 ④ 由③、④式可得s=2R
④ 由③、④式可得s=2R
从A到B过程,满足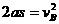 ⑤ ∴
⑤ ∴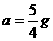
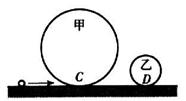 例7、如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一小球以一定的速度先滑上甲轨道,通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开两圆轨道。若小球在两圆轨道的最高点对轨道压力都恰好为零,试求水平CD段的长度。
例7、如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一小球以一定的速度先滑上甲轨道,通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开两圆轨道。若小球在两圆轨道的最高点对轨道压力都恰好为零,试求水平CD段的长度。
解析:(1)小球在光滑圆轨道上滑行时,机械能守恒,设小球滑过C点时的速度为 ,通过甲环最高点速度为v′,根据小球对最高点压力为零,由圆周运动公式有
,通过甲环最高点速度为v′,根据小球对最高点压力为零,由圆周运动公式有 ①
①
取轨道最低点为零势能点,由机械守恒定律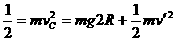 ②
②
由①、②两式消去v′,可得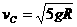
同理可得小球滑过D点时的速度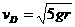 ,设CD段的长度为l,对小球滑过CD段过程应用动能定理
,设CD段的长度为l,对小球滑过CD段过程应用动能定理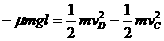 ,
,
将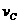 、
、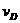 代入,可得
代入,可得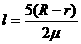
3、 动能定理有时可改写成守恒定律
2、 动能定理没有条件,机械能守恒定理有条件限制
1、 动能定理适用于任何物体(质点),机械能守恒定律适用于系统
5、动能定理与机械能守恒的联系
4、解题步骤
⑴确定研究对象和研究过程。⑵判断机械能是否守恒。⑶选定一种表达式,列式求解。
3、机械能守恒定律的各种表达形式
⑴初状态 = 末状态 ⑵ 增加量 = 减少量
用⑴时,需要规定重力势能的参考平面。用⑵时则不必规定重力势能的参考平面,因为重力势能的改变量与参考平面的选取没有关系。尤其是用ΔE增=ΔE减,只要把增加的机械能和减少的机械能都写出来,方程自然就列出来了。
2、对机械能守恒定律的理解:
①“守恒”是时时刻刻都相等。 ② “守恒”是“进出相等” ③要分清“谁”、“什么时候”守恒 ④、是否守恒与系统的选择有关 ⑤、⑴机械能守恒定律的研究对象一定是系统,至少包括地球在内。通常我们说“小球的机械能守恒”其实一定也就包括地球在内,因为重力势能就是小球和地球所共有的。另外小球的动能中所用的v,也是相对于地面的速度。
1、 条件
⑴在只有重力做功的情形下,物体的动能和重力势能发生相互转化,但机械能的总量保持不变。(和只受到重力不同)
⑵只有系统内的弹力做功,动能和弹性势能相互转化,机械能的总量保持不变。
(3) 其它力的总功为零,机械能守恒(举例:木块压缩弹簧)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com