1．描述天体运动的物理量主要有　　　 、　　　 、　　　 、　　　 与轨道半径

2．物体在地球表面所受的重力与万有引力的关系：若不考虑地球自转，物体在地球表面运行时有　　　　　 ，

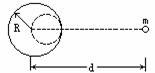　[例1] 如图所示，在一个半径为R、质量为M的均匀球体中，紧贴球的边缘挖去一个半径为R/2的球形空穴后，对位于球心和空穴中心连线上、与球心相距d的质点m的引力是多大？

[解析]把整个球体对质点的引力看成是挖去的小球体和剩余部分对质点的引力之和．其中完整的均质球体对球外质点m的引力这个引力可以看成是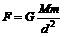：m挖去球穴后的剩余部分对质点的引力F₁与半径为R/2的小球对质点的引力F₂之和，即F=F₁+F₂．因半径为R/2的小球质量M^/为.

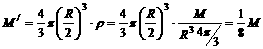则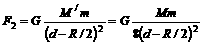

所以挖去球穴后的剩余部分对球外质点m的引力

.

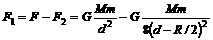
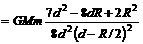[答案]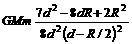

考点2　 与天体有关的估算问题

在估算有关天体的一些物理量时应紧扣两个关键：①掌握一串公式：　　　　　　　　　　　 ，以及质量公式　　　　　　　　　　 ．

②掌握一个模型：将天体或卫星的运动看成　　　　 运动，其向心力由　　　　 提供．

　[例2] (2009湛师附中)中国首个月球探测计划“嫦娥工程”预计在2017年送机器人上月球，实地采样送回地球，为载人登月及月球基地选址做准备。设想我国宇航员随“嫦娥”号登月飞船绕月球飞行，飞船上备有以下实验仪器：A.计时表一只，B.弹簧秤一把，C.已知质量为m的物体一个，D.天平一只(附砝码一盒)。在飞船贴近月球表面时可近似看成绕月做匀速圆周运动，宇航员测量出飞船在靠近月球表面的圆形轨道绕行N圈所用时间为t，飞船的登月舱在月球上着陆后，遥控机器人利用所携带的仪器又进行第二次测量，科学家利用上述两次测量数据便可计算出月球的半径和质量。若已知万有引力常量为G，则：

　　 (1)简述机器人是如何通过第二次测量物体在月球所受的重力F。

(2)试利用测量数据(用符号表示)球月球的半径和质量。

[解析] (1)利用弹簧秤测量物体m的重力F

(2)在月球近地表面有，，

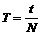
　　　 在月球表面有，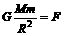　

　　　 则有　 　　，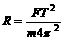

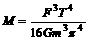
[答案](1)略(2)　 ，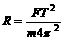

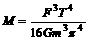
　[规律总结]万有引力定律在天文上的典型应用就是计算天体的质量、密度、半径，此时要紧口两个关键：一是紧扣一个物理模型：就是将天体(或卫星)的运动看成是匀速圆周运动；二是紧扣一个物体做圆周运动的动力学特征，即天体(或卫星)的向心力由万有引力提供．

考点3. 描述天体运动的物理量之间的关系、 卫星变轨问题

1．万有引力定律：

(1)内容：宇宙间的一切物体都是相互吸引的，两个物体间的引力大小，跟它们的　　 成　　　 正比，跟它们　　　 成反比．

(2)公式：　　　　　 ， G为万有引力常量，G=6.67×10^-11N.m²/kg²．

(3)适用条件：公式适用于　　　 间的相互作用．当两个物体间的距离　　 物体本身的大小时，物体可视为质点．

2．考点整合

考点1 万有引力定律基本公式的理解

1.考纲要求

10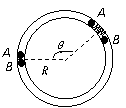．如图所示，水平面上固定着一个半径R=0.4m的 光滑环形轨道，在轨道内放入质量分别是M=0.2kg和m=0.1kg的小球A和 B(均可看成质点)，两球间夹一短弹簧。(1)开始时两球将弹簧压缩(弹簧的长度相对环形轨道半径和周长而言可忽略不计)，弹簧弹开后不动，两球沿轨道反向运动一段时间后又相遇，在此过程中，A球转过的角度θ是多少？(2)如果压缩弹簧在松手前的弹性势能E=1.2J，弹开后小球B在运动过程中受到光滑环轨道的水平侧压力是多大？

9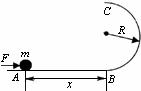．如图所示，光滑水平面右端B处连接一个竖直的半径为R的光滑半圆轨道，在离B距离为x的A点，用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力，质点沿半圆轨道运动到C处后又正好落回A点，求：

(1)推力对小球做了多少功? (用题中所给的量表示)

(2)x取何值时，完成上述运动所做的功最少?最小功为多少?

(3)x取何值时，完成上述运动所用的力最小?最小力为多少?

8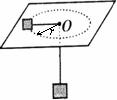．如图，细绳一端系着质量M=0.6kg的物体，静止在水平面，另一端通过光滑小孔吊着质量m=0.3kg的物体，M的中点与圆孔距离为0.2m，并知M和水平面的最大静摩擦力为2N，现使此平面绕中心轴线转动，问角速度ω，ω在什么范围M会处于静止状态? (g取10m/s²)

7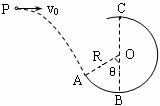．如图，一个质量为0.6kg 的小球以某一初速度从P点水平抛出，恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力，进入圆弧时无机械能损失)．已知圆弧的半径R=0.3m， θ=60 ⁰，小球到达A点时的速度 v=0.4 m/s ．(取g =10 m/s²)试求：

(1)小球做平抛运动的初速度v₀ ；

(2)P点与A点的水平距离和竖直高度；

(3)小球到达圆弧最高点C时，对轨道的压力．

6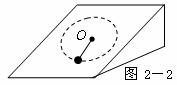． 如图2－2，一轻绳的一端系在固定粗糙斜面上的O点，另一端系一小球。给小球一足够大的初速度，使小球在斜面上做圆周运动。在此过程中(　 )

　　 A．小球的机械能守恒

B．重力对小球不做功

　　 C．绳的张力对小球不做功

D．在任何一段时间内，小球克服摩擦力所做的功总是等于小球动能的减少