

题目列表(包括答案和解析)
6. 一质量为M的探空气球在匀速下降,若气球所受浮力F始终保持不变,气球在运动过程中所受阻力仅与速率有关,重力加速度为g.现欲使该气球以同样速率匀速上升,则需从气球吊篮中减少的质量为( )
一质量为M的探空气球在匀速下降,若气球所受浮力F始终保持不变,气球在运动过程中所受阻力仅与速率有关,重力加速度为g.现欲使该气球以同样速率匀速上升,则需从气球吊篮中减少的质量为( )
A.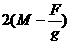 B.
B.
C.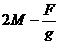 D. 0
D. 0
5.A、B、C三物体质量分别为M、m、m0,作如图所示的连接,绳子不可伸长,且绳子和滑轮的摩擦均不计,若B随A一起沿水平桌面向右做匀速运动,则可以断定( )
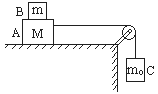 A.物体A与桌面之间有摩擦力,大小为m0g
A.物体A与桌面之间有摩擦力,大小为m0g
B.物体A与B之间有摩擦力,大小为m0g
C.桌面对A,B对A,都有摩擦力,方向相同,大小均为m0g
D.桌面对A,B对A,都有摩擦力,方向相反,大小均为m0g
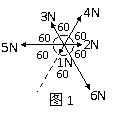
4.如图1所示,在同一平面内,大小分别为1N、2N、3N、4N、5N、 6N的六个力共同作用于一点,其合力大小为( )
 A.0
B.1N C.2N
D.3
A.0
B.1N C.2N
D.3
3. 右图是一种测定风力的仪器的原理图,质量为m的金属球,固定在一细长的轻金属丝下端,能绕悬点O在竖直平面内转动,无风时金属丝自然下垂,有风时金属丝将偏离竖直方向一定角度θ,角θ的大小与风力大小F有关,下列关于风力F与θ的关系式正确的是( )
右图是一种测定风力的仪器的原理图,质量为m的金属球,固定在一细长的轻金属丝下端,能绕悬点O在竖直平面内转动,无风时金属丝自然下垂,有风时金属丝将偏离竖直方向一定角度θ,角θ的大小与风力大小F有关,下列关于风力F与θ的关系式正确的是( )
A.F=mg·tanθ B.F=mg·sinθ
C.F=mg·cosθ D.F=mg∕cosθ
2.下列各组的三个点力,可能平衡的有 ( )
A.3N,4N,8N B.3N,5N,7N
C.1N,2N,4N D.7N,6N,13N
1.下列情况下,物体处于平衡状态的是( )
A.竖直上抛的物体到达最高点时 B.做匀速圆周运动的物体
C.单摆摆球摆到最高点时 D.水平弹簧振子通过平衡位置时
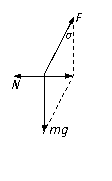
2. 在倾角为α的斜面上,一条质量不计的皮带一端固定在斜面上端,另一端绕过一中间有一圈凹槽的圆柱体,并用与斜面夹角为β的力拉住,使整个装置处于静止状态,如图10所示.不计一切摩擦,圆柱体质量为m,求拉力F的大小和斜面对圆柱体的弹力N的大小.
在倾角为α的斜面上,一条质量不计的皮带一端固定在斜面上端,另一端绕过一中间有一圈凹槽的圆柱体,并用与斜面夹角为β的力拉住,使整个装置处于静止状态,如图10所示.不计一切摩擦,圆柱体质量为m,求拉力F的大小和斜面对圆柱体的弹力N的大小.
某同学分析过程如下:
将拉力F沿斜面和垂直于斜面方向进行分解.
沿斜面方向: F cos β=mg sinα (1)
沿垂直于斜面方向: F sinβ+N=mg cos α (2)
问:你同意上述分析过程吗?若同意,按照这种分析方法求出F及N的大小;若不同意,指明错误之处并求出你认为正确的结果.
★ 抢分频道
◇限时基础训练
1. 用一轻绳将小球P系于光滑墙壁上的O点,在墙壁和球P之间夹有一矩形物块Q,如图所示.P、Q均处于静止状态,则下列相关说法正确的是
用一轻绳将小球P系于光滑墙壁上的O点,在墙壁和球P之间夹有一矩形物块Q,如图所示.P、Q均处于静止状态,则下列相关说法正确的是
A.P物体受4个力
B.Q受到3个力
C.若绳子变长,绳子的拉力将变小
D.若绳子变短,Q受到的静摩擦力将增大
2.多力平衡的基本解题方法:正交分解法
利用正交分解方法解体的一般步骤:(1)明确研究对象;(2)进行受力分析;(3)建立直角坐标系,建立坐标系的原则是让尽可能多的力落在坐标轴上,将不在坐标轴上的力正交分解;(4)x方向,y方向分别列平衡方程求解.
|
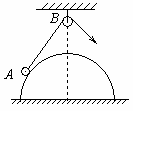 [例3]如图所示,固定在水平面上的光滑半球,球心O的正上方固定一个小定滑轮,细绳一端拴一小球,小球置于半球面上的A点,另一端绕过定滑轮,如图所示.今缓慢拉绳使小球从A点滑向半球顶点(未到顶点),则此过程中,小球对半球的压力大小N及细绳的拉力T大小的变化情况是 ( )
[例3]如图所示,固定在水平面上的光滑半球,球心O的正上方固定一个小定滑轮,细绳一端拴一小球,小球置于半球面上的A点,另一端绕过定滑轮,如图所示.今缓慢拉绳使小球从A点滑向半球顶点(未到顶点),则此过程中,小球对半球的压力大小N及细绳的拉力T大小的变化情况是 ( )
A.N变大,T变大 B.N变小,T变大
C.N不变,T变小 D.N变大,T变小
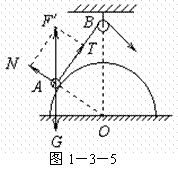 [解析]对A进行受力分析,如图所示,力三角形AF′N与几何三角形OBA相似,由相似三角形对应边成比例,解得N不变,T变小.
[解析]对A进行受力分析,如图所示,力三角形AF′N与几何三角形OBA相似,由相似三角形对应边成比例,解得N不变,T变小.
[答案]C
[规律总结]相似三角形法是解平衡问题时常遇到的一种方法,解题的关键是正确的受力分析,寻找力的矢量三角形和结构三角形相似.
[例4]倾角为θ的斜面上有质量为m 的木块,它们之间的动摩擦因数为μ.现用水平力F推动木块,如图所示,使木块恰好沿斜面向上做匀速运动.若斜面始终保持静止,求水平推力F的大小.
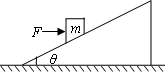 [解析]分析物体受力情况如图所示: 由于物体处于平衡状态,
[解析]分析物体受力情况如图所示: 由于物体处于平衡状态,
则有:
 沿斜面方向:
沿斜面方向: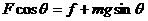
垂直与斜面方向: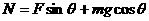
又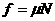
解得: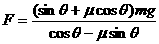
[规律总结]多力平衡问题宜采用正交分解法,采用正交分解法时,建立坐标系的原则是让尽可能多的力落在坐标轴上.
考点4 动态平衡
|
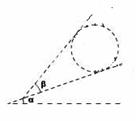
[例5]如图所示,在固定的、倾角为α斜面上,有一块可以转动的夹板(β不定),夹板和斜面夹着一个质量为m的光滑均质球体,试求:β取何值时,夹板对球的弹力最小.
[解析]解法一:图解法
对球体进行受力分析,然后对平行四边形中的矢量G和N1进行平移,使它们构成一个三角形,如图的左图和中图所示.
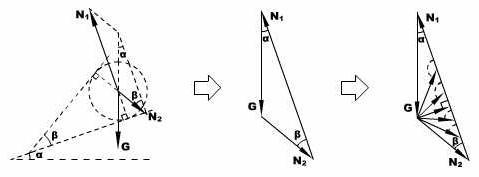
由于G的大小和方向均不变,而N1的方向不可变,当β增大导致N2的方向改变时,N2的变化和N1的方向变化如图中的右图所示.
显然,随着β增大,N1单调减小,而N2的大小先减小后增大,当N2垂直N1时,N2取极小值,且N2min = Gsinα.
解法二:解析法
看上图的中间图,对这个三角形用正弦定理,有: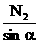 =
= 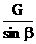 ,
,
即:N2 = 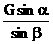 ,β在0到180°之间取值,N2的极值讨论是很容易的.
,β在0到180°之间取值,N2的极值讨论是很容易的.
[答案]当β= 90°时,甲板对球的弹力最小.
[规律总结]:求解三个力的动态平衡问题,一般是采用图解法,即先做出两个变力的合力(应该与不变的那个力等大反向)然后过合力的末端画方向不变的那个力的平行线,另外一个变力的末端必落在该平行线上,这样就能很直观的判断两个变力是如何变化的了,如果涉及到最小直的问题,还可以采用解析法,即采用数学求极值的方法求解.
考点5 连接体的平衡问题
|
[例6]有一个直角支架AOB,AO水平放置,表面粗糙, OB竖直向下, 表面光滑.AO上套有小环P,OB上套有小环Q,两环质量均为m,两环由一根质量可忽略、不可伸长的细绳相连,并在某一位置平衡,如图所示.现将P环向左移一小段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态比较,AO杆对P环的支持力FN和摩擦力f的变化情况是 ( )
表面光滑.AO上套有小环P,OB上套有小环Q,两环质量均为m,两环由一根质量可忽略、不可伸长的细绳相连,并在某一位置平衡,如图所示.现将P环向左移一小段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态比较,AO杆对P环的支持力FN和摩擦力f的变化情况是 ( )
A.FN不变,f变大 B.FN不变,f变小
 C.FN变大,f变大 D.FN变大,f变小
C.FN变大,f变大 D.FN变大,f变小
[解析]以两环和细绳整体为对象求FN,可知竖直方向上
始终二力平衡,FN=2mg不变;以Q环为对象,在重力、细
绳拉力F和OB压力N作用下平衡,如图,设细绳和竖直方向
的夹角为α,则P环向左移的过程中α将减小,N=mgtanα也将
减小.再以整体为对象,水平方向只有OB对Q的压力N和OA
对P环的摩擦力f作用,因此f=N也减小.
[答案]B
[规律总结]正确选取研究对象,可以使复杂的问题简单化,整体法是力学中经常用到的一种方法.
★ 高考重点热点题型探究
热点 共点力的平衡
[真题1]人站在自动扶梯的水平踏板上,随扶梯斜向上匀速运动,如图所示.以下说法正确的是( )
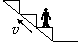 A.人受到重力和支持力的作用
A.人受到重力和支持力的作用
B.人受到重力、支持力和摩擦力的作用
C.人受到的合外力不为零
D.人受到的合外力方向与速度方向相同
[解析]人作匀速运动,故人所受合力为零,人所受重力和支持力均在竖直方向,故水平方向不应该受力,即人不受摩擦力作用.
[答案]A
[名师指引]本题考查平衡问题,属于基础题,切不可想当然认为人受到摩擦力.
 [真题2]如图,质量为M的楔形物块静置在水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦.用恒力F沿斜面向上拉小物块,使之匀速上滑.在小物块运动的过程中,楔形物块始终保持静止.地面对楔形物块的支持力为( )
[真题2]如图,质量为M的楔形物块静置在水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦.用恒力F沿斜面向上拉小物块,使之匀速上滑.在小物块运动的过程中,楔形物块始终保持静止.地面对楔形物块的支持力为( )
A.(M+m)g
B.(M+m)g-F
C.(M+m)g+Fsinθ
D.(M+m)g-Fsinθ
[解析]匀速沿斜面上升的小物体和斜面都处于平衡状态,可将二者看作一个处于平衡状态的整体,由竖直方向受力平衡可得: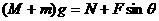 ,解得N=(M+m)g-Fsinθ
,解得N=(M+m)g-Fsinθ
[答案]D
[名师指引]本题因是求外界对系统的作用力,故将二者视为一整体来研究,将使求解变得简单,当然,本题也可以采用隔离法,同学们不妨一试.
[真题2]在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体A,A与竖直墙之间放一光滑圆球B,整个装置处于静止状态.现对B加一竖直向下的力F,F的作用线通过球心,设墙对B的作用力为F1,B对A的作用力为F2,地面对A的作用力为F3.若F缓慢增大而整个装置仍保持静止,截面如图所示,在此过程中( )
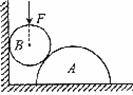 A.F1保持不变,F3缓慢增大
A.F1保持不变,F3缓慢增大
B.F1缓慢增大,F3保持不变
C.F2缓慢增大,F3缓慢增大
D.F2缓慢增大,F3保持不变
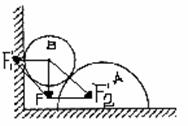 [解析]力F产生了两个作用效果,一个是使B压紧竖直墙面的力
[解析]力F产生了两个作用效果,一个是使B压紧竖直墙面的力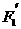 ,一个是压紧A的力
,一个是压紧A的力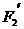 ,用整体法进行分析,可知
,用整体法进行分析,可知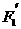 和地面对A的摩擦力大小相等,地面对A的支持力为
和地面对A的摩擦力大小相等,地面对A的支持力为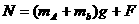 ,地面对A的作用力应指地面对A的摩擦力和支持力的合力,当力F缓慢增大时,
,地面对A的作用力应指地面对A的摩擦力和支持力的合力,当力F缓慢增大时,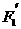 和
和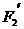 同时增大,故C正确
同时增大,故C正确
[答案]C
[名师指引]本题宜采用整体法和隔离法相结合来讨论,特别要理解地面对A的作用力应指地面对A的支持力和摩擦力的合力.
新题导练:
1.三力平衡的基本解题方法
(1)力的合成、分解法: 即分析物体的受力,把某两个力进行合成,将三力转化为二力,构成一对平衡力,二是把重力按实际效果进行分解,将三力转化为四力,构成两对平衡力. (参照上一讲考点3内容)
(2)相似三角形法: 利用矢量三角形与几何三角形相似的关系,建立方程求解力的方法.应用这种方法,往往能收到简捷的效果.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com