
题目列表(包括答案和解析)
7. 如图所示, MN是透镜的主轴, 点光源放在A点时, 成像于B点, 若将点光源放在B点, 则成像于C 点. 已知AB > BC, 以下关于透镜的种类和透镜位置的说法中正确的是
A. 透镜是凸透镜, 位于A点的左侧 ( )
B.  透镜是凹透镜, 位于C点的右侧
透镜是凹透镜, 位于C点的右侧
C. 透镜是凸透镜, 位于C点的右侧
D. 透镜是凹透镜, 位于A点的左侧
6. 发光物体沿凹透镜主光轴,从距透镜很远处向透镜移动。物体与它经透镜所成的像之间的距离的变化情况是 ( )
A. 逐渐增大 B. 逐渐减小 C. 先减小后增大 D. 先减小后增大
5.一凸透镜焦距为f,把物体从距透镜1.5f处移到2.5f处,则物像间的距离( )
A.一直变大 B.一直变小 C.先变大后变小 D.先变小后边大
4. 在下面的光路图中,OO′是透镜的主轴,M-N是透镜所在平面。由图中光线的偏折情况可以判断,其中肯定错误的是( )
在下面的光路图中,OO′是透镜的主轴,M-N是透镜所在平面。由图中光线的偏折情况可以判断,其中肯定错误的是( )
3.关于光学元件,以下说法正确的是( )
A.凸透镜是会聚透镜,任何光束经它后必定成为会聚光束
B.凹透镜是发散透镜,但有些光束经它后仍然会聚
C.三棱镜对白光有发散作用,所以平行光经过三棱镜后变为发散光
D.平面镜对光有反射作用,经平面镜反射后光的传播方向与原方向相反
2.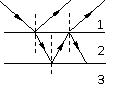 一束单色光在1、2、3三种介质中的两个平行界面处入射、反射、折射的情况如图所示. 若光在这三种介质中的光速分别用v1、v2、v3表示, 则下列关系式正确的是
( )
一束单色光在1、2、3三种介质中的两个平行界面处入射、反射、折射的情况如图所示. 若光在这三种介质中的光速分别用v1、v2、v3表示, 则下列关系式正确的是
( )
A. v1 > v2 > v3 B. v2 > v1 > v3
C. v2 > v3 > v1 D. v3 > v1 > v2
1. 入射光与镜面的夹角为600,当镜面转过150时,反射光线与入射光线夹角可能是
A. 30° B. 75° C. 90° D. 150° ( )
12、质量为m的钢板与直立轻弹簧的上端连接,弹簧下端固定在地上。平衡时,弹簧的压缩量为Xo,如图11-1所示。一物块从钢板正上方距离为 3Xo的A处自由落下,打在钢板上并立刻与钢板一起向下运动,但不粘连。它们到达最低点后又向上运动。已知物块质量也为m时,它们恰能回到O点。若物块质量为2m,仍从A处自由落下,则物块与钢板回到O点时,还具有向上的速度。求物块向上运动到达的最高点O点的距离。
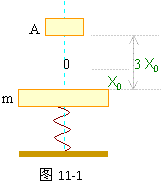 分析与解:物块自由下落,与钢板碰撞,压缩弹簧后再反弹向上,运动到O点,弹簧恢复原长。碰撞过程满足动量守恒条件。压缩弹簧及反弹时机械能守恒。自由下落3Xo,根据机械能守恒:
分析与解:物块自由下落,与钢板碰撞,压缩弹簧后再反弹向上,运动到O点,弹簧恢复原长。碰撞过程满足动量守恒条件。压缩弹簧及反弹时机械能守恒。自由下落3Xo,根据机械能守恒:
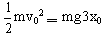 所以
所以 物块与钢板碰撞时,根据动量守恒: mv0=(m+m)v1(v1为碰后共同速度)
物块与钢板碰撞时,根据动量守恒: mv0=(m+m)v1(v1为碰后共同速度)
V1=V0/2=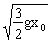
物块与钢板一起升到O点,根据机械能守恒: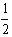 2mV12+Ep=2mgx0 [1]
2mV12+Ep=2mgx0 [1]
如果物块质量为2m,则:2mVo=(2m+m)V2 ,即V2=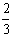 Vo
Vo
设回到O点时物块和钢板的速度为V,则: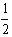 3mV22+Ep=3mgx0+
3mV22+Ep=3mgx0+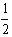 3mV2 [2]
3mV2 [2]
从O点开始物块和钢板分离,由[1]式得:
Ep=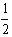 mgx0 代入[2]得:
mgx0 代入[2]得: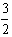 m(
m(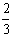 Vo)2+
Vo)2+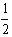 mgx0=3mgx0+
mgx0=3mgx0+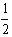 3mV2
3mV2
所以,V2=gx0
即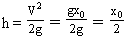
11、如图10-1所示,劲度系数为 K的轻质弹簧一端与墙固定,另一端与倾角为θ的斜面体小车连接,小车置于光滑水平面上。在小车上叠放一个物体,已知小车质量为 M,物体质量为m,小车位于O点时,整个系统处于平衡状态。现将小车从O点拉到B点,令OB=b,无初速释放后,小车即在水平面B、C间来回运动,而物体和小车之间始终没有相对运动。求:(1)小车运动到B点时的加速度大小和物体所受到的摩擦力大小。(2)b的大小必须满足什么条件,才能使小车和物体一起运动过程中,在某一位置时,物体和小车之间的摩擦力为零。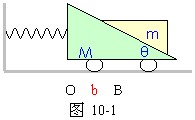
分析与解:
(1)所求的加速度a和摩擦力f是小车在B点时的瞬时值。取M、m和弹簧组成的系统为研究对象,由牛顿第二定律:kb=(M+m)a 所以a=kb/(M+m)。
取m为研究对象,在沿斜面方向有:f-mgsinθ=macosθ
所以,f=mgsinθ+m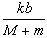 cosθ=m(gsinθ+
cosθ=m(gsinθ+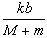 cosθ)
cosθ)
(2)当物体和小车之间的摩擦力的零时,小车的加速度变为a’,小车距O点距离为b’,取m为研究对象,有:mgsinθ=ma’cosθ
取M、m和弹簧组成的系统为研究对象,有:kb‘=(M+m)a’
以上述两式联立解得:b‘=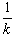 (M+m)gtgθ
(M+m)gtgθ
说明:在求解加速度时用整体法,在分析求解m受到的摩擦力时用隔离法。整体法和隔离法两者交互运用是解题中常用的方法,希读者认真掌握。
10、如图9-1所示,质量为M=3kg的木板静止在光滑水平面上,板的右端放一质量为m=1kg的小铁块,现给铁块一个水平向左速度V0=4m/s,铁块在木板上滑行,与固定在木板左端的水平轻弹簧相碰后又返回,且恰好停在木板右端,求铁块与弹簧相碰过程中,弹性势能的最大值EP。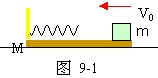
分析与解:在铁块运动的整个过程中,系统的动量守恒,因此弹簧压缩最大时和铁块停在木板右端时系统的共同速度(铁块与木板的速度相同)可用动量守恒定律求出。在铁块相对于木板往返运动过程中,系统总机械能损失等于摩擦力和相对运动距离的乘积,可利用能量关系分别对两过程列方程解出结果。
设弹簧压缩量最大时和铁块停在木板右端时系统速度分别为V和V’,由动量守恒得:mV0=(M+m)V=(M+m)V’ 所以,V=V’=mV0/(M+m)=1X4/(3+1)=1m/s
铁块刚在木板上运动时系统总动能为:EK=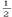 mV02=0.5X1X16=8J
mV02=0.5X1X16=8J
弹簧压缩量最大时和铁块最后停在木板右端时,系统总动能都为:
EK’=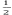 (M+m)V2=0.5X(3+1)X1=2J
(M+m)V2=0.5X(3+1)X1=2J
铁块在相对于木板往返运过程中,克服摩擦力f所做的功为:
Wf=f2L=EK-EK’=8-2=6J
铁块由开始运动到弹簧压缩量最大的过程中,系统机械能损失为:fs=3J
由能量关系得出弹性势能最大值为:EP=EK-EK‘-fs=8-2-3=3J
说明:由于木板在水平光滑平面上运动,整个系统动量守恒,题中所求的是弹簧的最大弹性势能,解题时必须要用到能量关系。在解本题时要注意两个方面:①.是要知道只有当铁块和木板相对静止时(即速度相同时),弹簧的弹性势能才最大;弹性势能量大时,铁块和木板的速度都不为零;铁块停在木板右端时,系统速度也不为零。
②.是系统机械能损失并不等于铁块克服摩擦力所做的功,而等于铁块克服摩擦力所做的功和摩擦力对木板所做功的差值,故在计算中用摩擦力乘上铁块在木板上相对滑动的距离。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com