
题目列表(包括答案和解析)
9. 如图所示,图A(a)中A、B是真空中相距为d的两平行金属板,在t=0时加上图(b)所示的交变电压,使开始时A板电势高于B板,这时在紧靠B板处有一初速为零的电子(质量为m,电量为e)在电场力作用下开始运动,欲使电子到达A板时具有最大的动能,则所加交变电压频率的最大值是多少?
如图所示,图A(a)中A、B是真空中相距为d的两平行金属板,在t=0时加上图(b)所示的交变电压,使开始时A板电势高于B板,这时在紧靠B板处有一初速为零的电子(质量为m,电量为e)在电场力作用下开始运动,欲使电子到达A板时具有最大的动能,则所加交变电压频率的最大值是多少?
fm=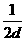
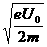
解析:图(b)中所示交变电压幅值不变,则金属板间电场强度大小不变,带电粒子所受电场力大小不变,只有方向做周期性变化。
欲使电子到达A板时速度是最大,须使电子从B板到A板的过程中一直加速,设电子由B板一直加速到A板所用时间为t ,则
d= at2=
at2=
 t2 → t=
t2 → t=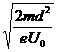
当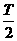 =t=
=t=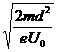 时 T为最小值,
时 T为最小值,
则Tmin=2d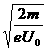
由f=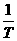 得 fmax=
得 fmax=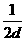
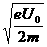 .
.
8. 在光滑的水平面上,有A、B两个物体,它们的质量分别为mA=4kg,mB=1kg,B物体与一轻弹簧相连,如图所示。若A、B分别具有动能EA、EB,且EA+EB=100J,问EA、EB各应为多少时,碰撞过程中弹簧的最大压缩量才能达到最大。
在光滑的水平面上,有A、B两个物体,它们的质量分别为mA=4kg,mB=1kg,B物体与一轻弹簧相连,如图所示。若A、B分别具有动能EA、EB,且EA+EB=100J,问EA、EB各应为多少时,碰撞过程中弹簧的最大压缩量才能达到最大。
A、B相向运动且EA=20J,EB=80J
解析:在碰撞过程中,当A、B两物体的速度相等时,弹簧的压缩量最大,此时弹簧的弹性势能最大,系统的动能最小。
设碰前A的速度为vA,B的速度为vB
若碰前A、B两物体运动方向相同,达共同速度时的速度为vAB,根据动量守恒定律有
mAvA+mBvB=(mA+mB)vAB
则碰后系统的总动能为EAB= (mA+mB)vAB2=
(mA+mB)vAB2=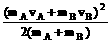 …………①
…………①
若碰前A、B两物体运动方向相反,由动量守恒得
mAvA-mBvB=(mA+mB)vAB
则碰后系统的总动能为EAB= (mA+mB)vAB2=
(mA+mB)vAB2=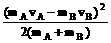 …………②
…………②
比较①②式可知,②式中当mAvA= mBvB时,EAB=0, 即EAB取得最小值,此时弹性势能达最大。
可知mAvA= mBvB …………③
又 mAvA2+
mAvA2+ mBvB2=100
…………④
mBvB2=100
…………④
③④联立并将mA=4kg, mB=1kg代入解得v1=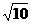 m/s, v2=4
m/s, v2=4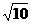 m/s
m/s
∴ EA=20J ,EB=80J
即两物体以大小相等,方向相反的动量相碰时,当弹簧压缩量最大时,速度为零,动能全部转化为弹性势能。
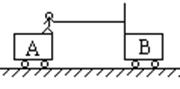
7.如图所示,水平地面上停放着A、B两辆小车,质量分别为M和m,M>m,两车相距为L。人的质量也为m,另有不计质量的一根竹杆和一根细绳。第一次人站在A车上,杆插在B车上,第二次人站在B车上,杆插在A车上。两种情况下,人用同样大小的力拉绳子,使两车相遇。设阻力可忽略不计,两次小车从开始运动到相遇的时间分别为t1和t2,则 ( )
 A.t1>t2 B.t1<t2
A.t1>t2 B.t1<t2
C.t1=t2 D.条件不足,无法判断
B
解析:当人用力拉绳子时,两小车均做匀加速运动,设人的拉力大小为F。
解法一:当人站在A车拉绳子时,A车的加速度大小为aA=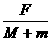 ,B车的加速度大小为aB=
,B车的加速度大小为aB=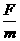 ,设相遇时A车运动的位移大小为
,设相遇时A车运动的位移大小为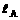 ,B车的位移大小为
,B车的位移大小为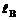 则
则
 =
= aAt12=
aAt12=
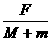 t12 ………………①
t12 ………………①
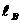 =
= aBt12=
aBt12=
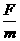 t22
………………②
t22
………………②
而 +
+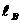 =
=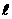 ……………………③
……………………③
由①②③得t1=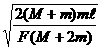 ………………④
………………④
当人站要B车上拉绳子时aA=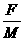 ,aB=
,aB= 同理可得
同理可得
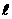 =
= +
+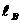 =
= aAt22+
aAt22+ aBt22=
aBt22=
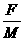 t22+
t22+
 t22
t22
即t2=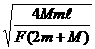 ………………⑤
………………⑤
比较④⑤,由于M>m,则M+m<2M, 知t1<t2
解法二:第一次人站在A车上拉绳子,设拉力大小为F,则
A车加速度大小 aA=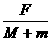 ,B车加速度大小 aB=
,B车加速度大小 aB=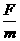
则A车相对B车加速度大小为 a相=aA+aB=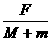 +
+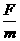 =
=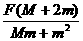
第二次人站在B车上,拉力大小仍为F,则
A车加速度大小 =
=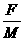 ,B车加速度大小
,B车加速度大小
 =
=
于是A车相对B车加速度大小为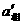 =
= +
+ =
=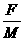 +
+ =
=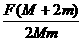 由于M>m,容易看出a相>
由于M>m,容易看出a相>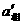
由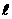 =
= a相t12 及
a相t12 及
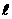 =
=
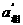 t22
t22
解得t1<t2.
解法三:采用极限法分析。由于题设条件M>m,假设M→∞,则前后两种情况下A车不动,只需考虑B车的运动。
第一次人站在A车上用F力拉绳子,则B车加速度大小为
aB=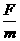
第二次人站在B车上用F力拉绳子,则B车加速度大小为
aA=
显然aB > aA,所以t1<t2。
6. 如图所示,一辆有
如图所示,一辆有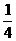 圆弧的小车停在粗糙的水平地面上,质量为m的小球从静止开始由车顶无摩擦地滑下,在小球下滑过程中小车始终保持静止状态,求:
圆弧的小车停在粗糙的水平地面上,质量为m的小球从静止开始由车顶无摩擦地滑下,在小球下滑过程中小车始终保持静止状态,求:
⑴当小车运动到什么位置时,地面对小车的静摩擦力最大?
⑵地面对小车静摩擦力的最大值为多少?
⑴小球与圆心O连线与竖直方向夹角为450 ⑵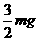
解析:设圆弧半径为R,当小球运动到支持力N与竖直方向的夹角为θ时,速度为v,此时小球受力如图甲所示,由牛顿第二律及圆周运动知识知:
N-mgcosθ=m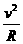 ……①
……①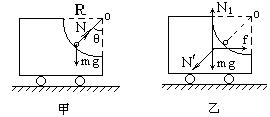
由机械能守恒定律得:
mgRcosθ= mv2……②
mv2……②
联立①②解得:N=3mgcosθ……③
小车受力如图乙所示,由平衡条件知,车所受地面的摩擦力 f=N·sinθ,将③式入得f=3mgcosθ·sinθ=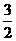 mgsin2θ,当θ=450时,sin2θ=1最大。
mgsin2θ,当θ=450时,sin2θ=1最大。
则可得静摩擦力的最大值为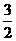 mg。
mg。
0.4N
解析:欲使推力最小,应满足撤去推力后,米尺继续向前滑行,至米尺的中心恰好到桌边时,米尺的速度为零。
设最小的水平推力为Fm,1s内米尺的位移为s1,1s末米尺的速度为v,以运动方向为正,有
Fm-μmg=ma1 → a1=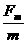 -μg
-μg
s1= a1t12=
a1t12= (
(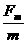 -μg)×12=
-μg)×12= (
(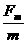 -μg)
-μg)
v=a1t=(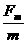 -μg)·1=
-μg)·1=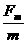 -μg
-μg
撤去推力后,米尺在摩擦力作用下向前减速滑行了位移S2时速度减为零,有
-μmg=ma2 → a2=-μg=-1.6m/s2
0-v2=2a2s2 → s2=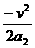 =
=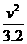
由题意知:s1+s2=0.25m,则有:
 (
(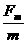 -μg)+
-μg)+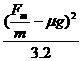 =0.25
=0.25
代入数据并整理得: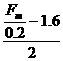 +
+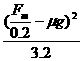 =0.25
=0.25
即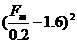 +1.6(
+1.6(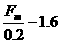 )-0.8=0
)-0.8=0
设y=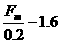 ,则上式可化为:y2+1.6y-0.8=0
,则上式可化为:y2+1.6y-0.8=0
解得y=0.4
可知: 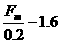 =0.4 即 Fm=0.4N
=0.4 即 Fm=0.4N
错解分析:有人用F-μmg=ma,得出a=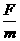 -μg,再用s=
-μg,再用s= at2=
at2= (
(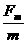 -μg)t2,将s=0.25m、m=0.2kg、μ=0.16、t=1s代入解得F=0.42N。其错误原因是使米尺在1s内一直加速并当尺的重心到桌边时有最大速度。
-μg)t2,将s=0.25m、m=0.2kg、μ=0.16、t=1s代入解得F=0.42N。其错误原因是使米尺在1s内一直加速并当尺的重心到桌边时有最大速度。
5.一根质量为0.2kg,粗细均匀的米尺放在水平桌面上,它与桌面的动摩擦因数为0.16,开始时,尺子有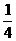 露出桌边。今用一水平推力作用1s时间,使尺从桌边掉下,g取10m/s2,问水平推力至少多大?
露出桌边。今用一水平推力作用1s时间,使尺从桌边掉下,g取10m/s2,问水平推力至少多大?
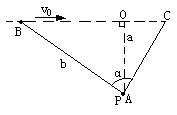
4.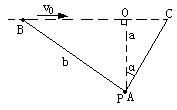 如图所示,A船从港口P出发,拦截正以速度v0沿直线航行的船B,P与B所在的航线的垂直距离为a,A船起航时,B与P的距离为b,且b>a,如略去A船起动时的加速过程,认为它一起航就做匀速运动,求A船能拦到B船所需的最小速度v。
如图所示,A船从港口P出发,拦截正以速度v0沿直线航行的船B,P与B所在的航线的垂直距离为a,A船起航时,B与P的距离为b,且b>a,如略去A船起动时的加速过程,认为它一起航就做匀速运动,求A船能拦到B船所需的最小速度v。
vmin=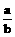 v0 , 运动方向应与A、B两船开始时位置的连线垂直。
v0 , 运动方向应与A、B两船开始时位置的连线垂直。
解析:
方法一:设A船的速度为v,运动方向与PO的夹角α,由两船运动的时间相等并结合图示的几何关系得
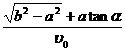 =
=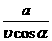
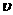 =
=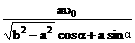
设tanβ=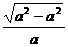 ,则上式为v=
,则上式为v=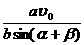
显然,当α+β=90°时,A船的速率最小,最小值为vmin=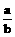 v0。结合图示得到:A船的运动方向应与A、B两船开始时位置的连线垂直。
v0。结合图示得到:A船的运动方向应与A、B两船开始时位置的连线垂直。
 方法二:设A船的速度为v,运动方向与A、B连线的夹角α,由两船运动的时间相等并结合正弦定理得
方法二:设A船的速度为v,运动方向与A、B连线的夹角α,由两船运动的时间相等并结合正弦定理得
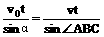
由于∠ABC及v0为定值,只有当α=90°时,A船的速率最小,此时,最小值为vmin=
v0sin∠ABC=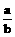 v0。
v0。
方法三:以B船为参照物,欲使A船能拦截到B船,A船应正对B船运动,即A船相对于B船的速度方向应由A指向B。
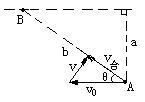 由于大地相对于B的速度为v0,方向与B船相对于地面的速度方向相反,设A船相对于B船的速度v合,大地对B的速度为v0,A对地的速度为v,满足
由于大地相对于B的速度为v0,方向与B船相对于地面的速度方向相反,设A船相对于B船的速度v合,大地对B的速度为v0,A对地的速度为v,满足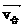 =
=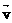 +
+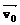 ,由图可看出,只有当v与v合方向垂直时,v才最小。
,由图可看出,只有当v与v合方向垂直时,v才最小。
由sinθ=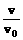 =
=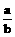
解得vmin=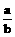 v0
v0
3.质量为10㎏的物体在倾角为300的斜面上恰能匀速下滑。欲使该物体产生大小为a=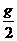 ,方向沿斜面向上的加速度,需对物体施加一个拉力,求推力F的最小值Fmin为多少?
,方向沿斜面向上的加速度,需对物体施加一个拉力,求推力F的最小值Fmin为多少?
Fmin=129.9N 方向与斜面成300角斜向上。
解析:由物体沿斜面匀速下滑,可知动摩擦因数µ=tan300 =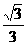 。
。
当物体以a=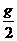 沿斜面向上做匀加速运动时,物体受四个力:重力㎎ 、支持力N、摩擦力ƒ和推力F,其合力F合=ma
=
沿斜面向上做匀加速运动时,物体受四个力:重力㎎ 、支持力N、摩擦力ƒ和推力F,其合力F合=ma
= ㎎.设摩擦力ƒ和支持力N的合力为F1,则F1与N的夹角为θ= arc tanµ=300,做出物体的受力矢量图,如图所示。
㎎.设摩擦力ƒ和支持力N的合力为F1,则F1与N的夹角为θ= arc tanµ=300,做出物体的受力矢量图,如图所示。
 从图可看出,重力㎎、F1与拉力F的合力为F合。由于㎎、F合大小方向一定,而F1的方向一定,只有当F与F1垂直时推力F才最小。
从图可看出,重力㎎、F1与拉力F的合力为F合。由于㎎、F合大小方向一定,而F1的方向一定,只有当F与F1垂直时推力F才最小。
∵∠DAB=600 ∠BDA=∠ODC=300
∴
∠OCD=300 OD=OC= ㎎ DA=
㎎ DA= ㎎
㎎
则Fmin=  ㎎cos300
+2
㎎cos300
+2  ㎎cos300
=
㎎cos300
=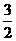 ㎎cos300
=129.9N
㎎cos300
=129.9N
2.质量为m的物体放在水平地面上,物体与地面间的动摩擦因数μ=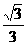 ,当物体在地面上做匀速直线运动时,需要加一个外力F,此力的最小值为多少?方向如何?
,当物体在地面上做匀速直线运动时,需要加一个外力F,此力的最小值为多少?方向如何?
 ㎎.
㎎.
解析:
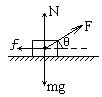 (1)用函数法求解:设所加的拉力F与水平方向的夹角为θ,受力如图所示。则
(1)用函数法求解:设所加的拉力F与水平方向的夹角为θ,受力如图所示。则
F cosθ-μ(㎎-Fsinθ)=0.
即F=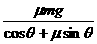 而μ=
而μ=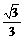 =tan300
=tan300
则 F=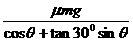 =
=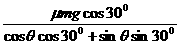 =
=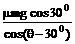
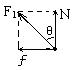 当θ=300 F最小,最小值为Fmin=μ㎎cos300 =
当θ=300 F最小,最小值为Fmin=μ㎎cos300 = ㎎.
㎎.
 (2)用图解法求解:物体相对地面滑动时,满足摩擦定律ƒ=µFN。 即µ=
(2)用图解法求解:物体相对地面滑动时,满足摩擦定律ƒ=µFN。 即µ=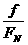 。设ƒ与N的合力为F1,则不论支持力N如何变化,摩擦力ƒ与支持力N的比值µ不变,
如图所示中的θ不变。题中tanθ= µ =
。设ƒ与N的合力为F1,则不论支持力N如何变化,摩擦力ƒ与支持力N的比值µ不变,
如图所示中的θ不变。题中tanθ= µ =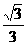 ,θ =300
.
,θ =300
.
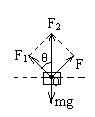
本题中物体的受力可做如下等效变化:重力㎎、支持力与摩擦力的合力
F1、拉力F,如图所示:
由于F1与F的合力F2总与㎎等大反向且F1的方向不变,由矢量三角形OFF2可得:只有当F与F1垂直时,F才最小。
F min=F2sinθ= ㎎, 且F与水平方向的夹角为θ=30°。
㎎, 且F与水平方向的夹角为θ=30°。
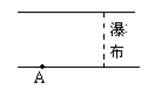
1.如图所示,一条平直的河流宽为80m,河水流速为8 m/s,一人驾驶一动力渔船,欲从河岸的A点渡河到对岸 ,已知在A点的下游60 m处有一与河岸垂直的瀑布,人欲安全渡河,渔船的最小划行速度为多少?
 船速大小为6.4m/s ,方向与河岸成θ=370
船速大小为6.4m/s ,方向与河岸成θ=370
解析:如图所示,欲使船安全渡河,则船在河中合速度v的极限方向是指向瀑布边缘与对岸的交点B,由于v是水流速v0与船速v1的合速度,由速度矢量三角形Av0C可知,只有v0C与AB垂直,即船速v1与AB垂直时v1才最小。
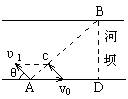 设
v1与河岸夹角为θ,则
设
v1与河岸夹角为θ,则
v1=v0cosθ
而在ΔABD中cosθ=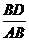
将v0=8m/s BD=80m AD=60m 代入解得
v1=6.4m/s θ=370
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com