13．解：(1)在D点，速度为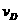，则有

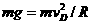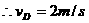　　　　 　　　 1分

　　　　 　　　　 1分

　　　　 由A运动到D点，机械能守恒

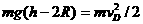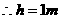　　　　 　　　 1分

　　　　 　　 1分

　 (2)由A运动到C点，机械能守恒

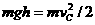　　　　 　　　 1分

　　　　 在C点，由向心力公式，得

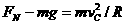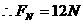　　　　 　　　 1分

　　　　 　　　　 1分

　　　　 由牛顿第三定律得压力为12N　　　 1分

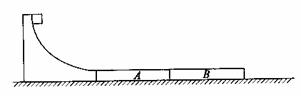
16．(16分)如图所示，某货场利用固定于地面的、半径R=1．8m的四分之一圆轨道将质量为m₁=10 kg的货物(可视为质点)从高处运送至地面，已知当货物由轨道顶端无初速滑下时，到达轨道底端的速度为5 m／s．为避免货物与地面发生撞击，在地面上紧靠轨道依次排放两块完全相同的木板A、B，长度均为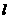=2 m，质量均为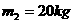，木板上表面与轨道末端相切．货物与木板间的动摩擦因数为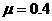，木板与地面间的动摩擦因数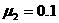．(最大静摩擦力与滑动摩擦力大小相等，取g=10 m／s²)

　 (1)求货物沿圆轨道下滑过程中克服摩擦力做的功

　 (2)通过计算判断货物是否会从木板B的右端滑落?若能，求货物滑离木板B右端时的速度；若不能，求货物最终停在B板上的位置．

[2010济南一模答案]

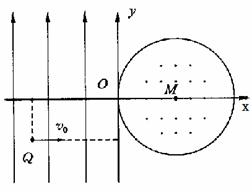
15．(12分)如图所示，在平面坐标系xoy内，第Ⅱ、Ⅲ象限内存在沿y轴正方向的匀强电场，第I、Ⅳ象限内存在半径为L的圆形匀强磁场，磁场圆心在M(L，0)点，磁场方向垂直于坐标平面向外．一带正电粒子从第Ⅲ象限中的Q(一2L，一L)点以速度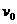沿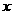轴正方向射出，恰好从坐标原点O进入磁场，从P(2L，O)点射出磁场．不计粒子重力，求：

　 (1)电场强度与磁感应强度大小之比

　 (2)粒子在磁场与电场中运动时间之比

14．(12分)如图所示，宽度为L=0．20 m的足够长的平行光滑金属导轨固定在绝缘水平桌面上，导轨的一端连接阻值为R=0．9的电阻．导轨cd段右侧空间存在垂直桌面向上的匀强磁场，磁感应强度B=0．50 T．一根质量为m=10 g，电阻r=0．1的导体棒ab垂直放在导轨上并与导轨接触良好．现用一平行于导轨的轻质细线将导体棒ab与一钩码相连，将重物从图示位置由静止释放．当导体棒ab到达cd时，钩码距地面的高度为h=0．3 m．已知导体棒ab进入磁场时恰做v=10 m／s的匀速直线运动，导轨电阻可忽略不计，取g=10 m／s²．求：

　 (1)导体棒ab在磁场中匀速运动时，闭合回路中产生的感应电流的大小

　 (2)挂在细线上的钩码的重力大小

　 (3)求导体棒ab在磁场中运动的整个过程中电阻R上产生的热量

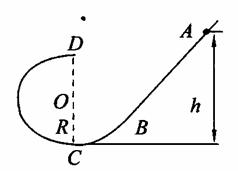
13．(8分)如图所示，光滑圆弧轨道与光滑斜面在B点平滑连接，圆弧半径为R=0．4 m，一半径很小、质量为m=0．2 kg的小球从光滑斜面上A点由静止释放，恰好能通过圆弧轨道最高点D，g取10 m／s²．求：

　 (1)小球最初离最低点C的高度；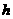

　 (2)小球运动到C点时对轨道的压力大小F_N。

15．(1)0.82MeV　 ………………3分

　 (2)①据动量守恒定律：　 ………………3分

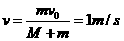　 ………………2分

②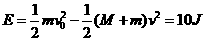　 ………………2分

[2010济南一模]

12．(16分)

解：(1)由几何关系和运动合成知识可知：

粒子离开电场时的速度的大小

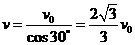　 ………………2分

　 (2)根据类平抛运动的规律有：

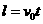　 ………………2分

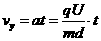　 ………………2分

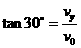　　 ………………2分

联立，解得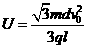：　 ………………1分

　 (3)由几何关系得：

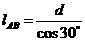　 ………………1分

粒子在磁场中做圆周运动的轨道半径为：

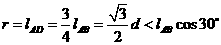　 ………………2分

故能够从AC边垂直射出　 ………………1分

设三角形区域内磁感应强度为B，根据向心力公式有：

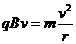　 ………………2分

解得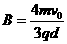：　 ………………1分

11．(14分)

　　 解：(1)设小球经过B点时的速度大小为；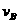

由机械能守恒得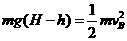：　 ………………2分

求得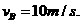：　 ………………2分

　 (2)设小球经过C点时的速度为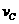，对轨道的压力为N，则轨道对小球的压力N

由机械能守恒得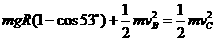：　 …………2分

联立，解得：N=43N。　 ………………1分

方向：竖直向下　 ………………1分

　 (3)设小球由D到达S的过程中阻力所做的功为W，

易知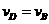，　 ………………1分

由动能定理可得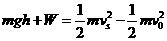：　 …………2分

代入数据，解得得W=-68J。　 ………………1分

15．(本题共10分)

　 (1)雷蒙德·戴维斯因研究来自太阳的电子中微子(v₀)而获得了2002年度诺贝尔物理学奖．他探测中微子所用的探测器的主体是一个贮满615吨四氯乙烯( C₂Cl₄)溶液巨桶．电子中微子可以将一个氯核转变为一个氩核，其核反应方程式为

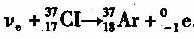
已知Cl核的质量为36.95658 u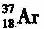，核的质量为36.95691 u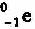．的质量为0.00055u，1u厦量对应的能量为931.5MeV．根据以上数据，可以判断参与上述反应的电子中微子的最小能量为　　　 MeV(结果保留两位有效数字)．

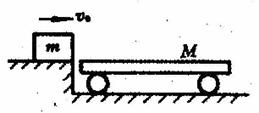
　 (2)如图所示，质量为m=1kg的滑块，以v₀ =5m/s的水平初速度滑上静止在光滑水平面的平板小车，小车足够长，质量M=4kg求：

①滑块与小车的共同速度v

②整个运动过程中产生的内能E

[2010淄博一模答案]

12．(16分)

两块平行金属板MN、PQ水平放置，两板间距为d、板长为l，在紧靠平行板右侧的正三角形区域内存在着垂直纸面向里的匀强磁场，三角形底边BC与PQ在同一水平线上，顶点A与MN在同一水平线上，如图所示．一个质量为m、电量d/4的带正电的粒子以初速度%水平射入两金属板之间，入射点到上极板的距离为d/4若在两板间加某一恒定电压，粒子离开电场后垂直AB边从点进入磁场，并垂直AC边射出(不计粒子的重力)．已知BD=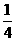AB求：

　 (1)粒子离开电场时的瞬时速度的大小；

　 (2)两极板间电压；

　 (3)三角形区域内磁感应强度的大小