
题目列表(包括答案和解析)
23.(浙江卷) (20分)如图所示,一矩形轻质柔软反射膜可绕过O点垂直纸面的水平轴转动,其在纸面上的长度为L1,垂直的为L2。在膜的下端(图中A处)挂有一科行于转轴,质量为m,长为L3的导体棒使膜*成平面。在膜下方水平放置一足够大的太阳能光电池板,能接收到经反射膜反射到光电池板上的所有光能,并将沟通转化成电能。光电池板可等效为一个一电池,输出电压恒定为U;输出电流正比于光电池板接收到的光能(设垂直于入身光单位面积上的光功率保持恒定)。导体棒处在方向竖直向上的匀强磁场B中,并与光电池构成回路,流经导体棒的电流垂直纸面向外(注:光电池与导体棒直接相连,连接导线未画出)。
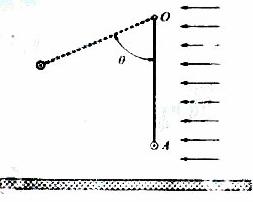
(1)再有一束平等光水平入射,当反射膜与竖直方向成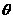 =60
=60 时,导体棒牌受力平衡状态,求此时电流强度的大小和光电池的输出功率。
时,导体棒牌受力平衡状态,求此时电流强度的大小和光电池的输出功率。
(2)当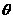 变成45
变成45 时,通过调整电路使导体棒保持平衡,光电池除维持导体棒国学平衡外,不能输出多少额外电功率?
时,通过调整电路使导体棒保持平衡,光电池除维持导体棒国学平衡外,不能输出多少额外电功率?
解析:
(1)导体棒所受安培力
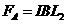 ①
①
导体棒有静力平衡关系 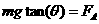 ②
②
解得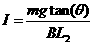 ③
③
所以当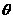 =60°时,
=60°时,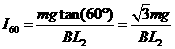
光电池输出功率为 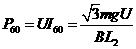
(2)当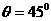 时,根据③式可知维持静力平衡需要的电流为
时,根据③式可知维持静力平衡需要的电流为

根据几何关系可知 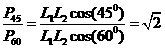
可得 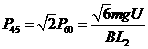
12.(天津卷)(20分)质谱分析技术已广泛应用于各前沿科学领域。汤姆孙发现电子的质谱装置示意如图,M、N为两块水平放置的平行金属极板,板长为L,板右端到屏的距离为D,且D远大于L,O’O为垂直于屏的中心轴线,不计离子重力和离子在板间偏离O’O的距离。以屏中心O为原点建立xOy直角坐标系,其中x轴沿水平方向,y轴沿竖直方向。
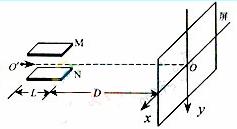
(1)设一个质量为m0、电荷量为q0的正离子以速度v0沿O’O的方向从O’点射入,板间不加电场和磁场时,离子打在屏上O点。若在两极板间加一沿+y方向场强为E的匀强电场,求离子射到屏上时偏离O点的距离y0;
(2)假设你利用该装置探究未知离子,试依照以下实验结果计算未知离子的质量数。
上述装置中,保留原电场,再在板间加沿-y方向的匀强磁场。现有电荷量相同的两种正离子组成的离子流,仍从O’点沿O’O方向射入,屏上出现两条亮线。在两线上取y坐标相同的两个光点,对应的x坐标分别为3.24mm和3.00mm,其中x坐标大的光点是碳12离子击中屏产生的,另一光点是未知离子产生的。尽管入射离子速度不完全相同,但入射速度都很大,且在板间运动时O’O方向的分速度总是远大于x方向和y方向的分速度。
解析:(1)离子在电场中受到的电场力
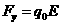 ①
①
离子获得的加速度
 ②
②
离子在板间运动的时间
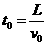 ③
③
到达极板右边缘时,离子在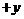 方向的分速度
方向的分速度
 ④
④
离子从板右端到达屏上所需时间
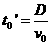 ⑤
⑤
离子射到屏上时偏离 点的距离
点的距离
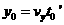
由上述各式,得
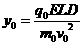 ⑥
⑥
(2)设离子电荷量为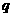 ,质量为
,质量为 ,入射时速度为
,入射时速度为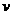 ,磁场的磁感应强度为
,磁场的磁感应强度为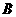 ,磁场对离子的洛伦兹力
,磁场对离子的洛伦兹力
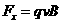 ⑦
⑦
已知离子的入射速度都很大,因而离子在磁场中运动时间甚短,所经过的圆弧与圆周相比甚小,且在板间运动时,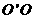 方向的分速度总是远大于在
方向的分速度总是远大于在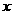 方向和
方向和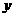 方向的分速度,洛伦兹力变化甚微,故可作恒力处理,洛伦兹力产生的加速度
方向的分速度,洛伦兹力变化甚微,故可作恒力处理,洛伦兹力产生的加速度
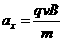 ⑧
⑧
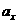 是离子在
是离子在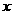 方向的加速度,离子在
方向的加速度,离子在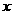 方向的运动可视为初速度为零的匀加速直线运动,到达极板右端时,离子在
方向的运动可视为初速度为零的匀加速直线运动,到达极板右端时,离子在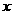 方向的分速度
方向的分速度
 ⑨
⑨
离子飞出极板到达屏时,在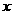 方向上偏离
方向上偏离 点的距离
点的距离
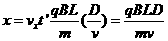 ⑩
⑩
当离子的初速度为任意值时,离子到达屏上时的位置在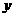 方向上偏离
方向上偏离 点的距离为
点的距离为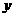 ,考虑到⑥式,得
,考虑到⑥式,得
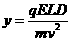 ⑾
⑾
由⑩、⑾两式得
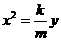 ⑿
⑿
其中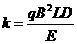
上式表明,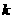 是与离子进入板间初速度无关的定值,对两种离子均相同,由题设条件知,
是与离子进入板间初速度无关的定值,对两种离子均相同,由题设条件知,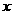 坐标3.24mm的光点对应的是碳12离子,其质量为
坐标3.24mm的光点对应的是碳12离子,其质量为 ,
,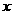 坐标3.00mm的光点对应的是未知离子,设其质量为
坐标3.00mm的光点对应的是未知离子,设其质量为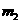 ,由⑿式代入数据可得
,由⑿式代入数据可得
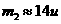 ⒀
⒀
故该未知离子的质量数为14。
23.(北京卷)(18分)利用霍尔效应制作的霍尔元件以及传感器,广泛应用于测量和自动控制等领域。
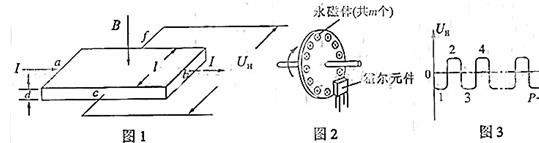
如图1,将一金属或半导体薄片垂直至于磁场B中,在薄片的两个侧面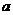 、
、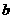 间通以电流
间通以电流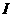 时,另外两侧
时,另外两侧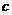 、
、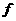 间产生电势差,这一现象称霍尔效应。其原因是薄片中的移动电荷受洛伦兹力的作用相一侧偏转和积累,于是
间产生电势差,这一现象称霍尔效应。其原因是薄片中的移动电荷受洛伦兹力的作用相一侧偏转和积累,于是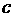 、
、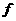 间建立起电场EH,同时产生霍尔电势差UH。当电荷所受的电场力与洛伦兹力处处相等时,EH和UH达到稳定值,UH的大小与
间建立起电场EH,同时产生霍尔电势差UH。当电荷所受的电场力与洛伦兹力处处相等时,EH和UH达到稳定值,UH的大小与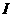 和
和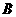 以及霍尔元件厚度
以及霍尔元件厚度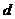 之间满足关系式
之间满足关系式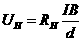 ,其中比例系数RH称为霍尔系数,仅与材料性质有关。
,其中比例系数RH称为霍尔系数,仅与材料性质有关。
(1)设半导体薄片的宽度(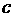 、
、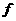 间距)为
间距)为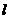 ,请写出UH和EH的关系式;若半导体材料是电子导电的,请判断图1中
,请写出UH和EH的关系式;若半导体材料是电子导电的,请判断图1中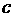 、
、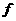 哪端的电势高;
哪端的电势高;
(2)已知半导体薄片内单位体积中导电的电子数为n,电子的电荷量为e,请导出霍尔系数RH的表达式。(通过横截面积S的电流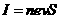 ,其中
,其中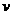 是导电电子定向移动的平均速率);
是导电电子定向移动的平均速率);
(3)图2是霍尔测速仪的示意图,将非磁性圆盘固定在转轴上,圆盘的周边等距离地嵌装着m个永磁体,相邻永磁体的极性相反。霍尔元件置于被测圆盘的边缘附近。当圆盘匀速转动时,霍尔元件输出的电压脉冲信号图像如图3所示。
a.若在时间t内,霍尔元件输出的脉冲数目为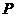 ,请导出圆盘转速
,请导出圆盘转速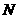 的表达式。
的表达式。
b.利用霍尔测速仪可以测量汽车行驶的里程。除除此之外,请你展开“智慧的翅膀”,提出另一个实例或设想。
解析:
(1)由 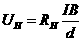 ①
①
得  ②
②
当电场力与洛伦兹力相等时 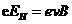 ③
③
得
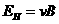 ④
④
将 ③、④代入②,
得 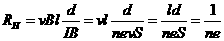
(2) a.由于在时间t内,霍尔元件输出的脉冲数目为P,则
P=mNt
圆盘转速为
N=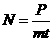
b.提出的实例或设想
25.(山东卷)(18分)如图所示,以两虚线为边界,中间存在平行纸面且与边界垂直的水平电场,宽度为d,两侧为相同的匀强磁场,方向垂直纸面向里。一质量为 、带电量+q、重力不计的带电粒子,以初速度
、带电量+q、重力不计的带电粒子,以初速度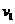 垂直边界射入磁场做匀速圆周运动,后进入电场做匀加速运动,然后第二次进入磁场中运动,此后粒子在电场和磁场中交替运动。已知粒子第二次在磁场中运动的半径是第一次的二倍,第三次是第一次的三倍,以此类推。求
垂直边界射入磁场做匀速圆周运动,后进入电场做匀加速运动,然后第二次进入磁场中运动,此后粒子在电场和磁场中交替运动。已知粒子第二次在磁场中运动的半径是第一次的二倍,第三次是第一次的三倍,以此类推。求

⑴粒子第一次经过电场子的过程中电场力所做的功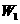 。
。
⑵粒子第n次经过电场时电场强度的大小 。
。
⑶粒子第n次经过电场子所用的时间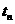 。
。
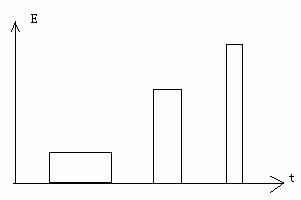
⑷假设粒子在磁场中运动时,电场区域场强为零。请画出从粒子第一次射入磁场至第三次离开电场的过程中,电场强度随时间变化的关系图线(不要求写出推导过程,不要求标明坐标明坐标刻度值)。
解析:
(1)根据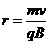 ,因为
,因为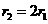 ,所以
,所以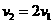 ,所以
,所以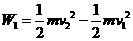 ,
,
(2)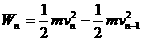 =
=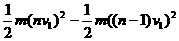 ,
,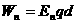 ,所以
,所以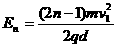 。
。
(3)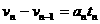 ,
,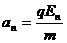 ,所以
,所以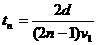 。
。
(4)
36.(广东卷)(18分)如图16(a)所示,左为某同学设想的粒子速度选择装置,由水平转轴及两个薄盘N1、N2构成,两盘面平行且与转轴垂直,相距为L,盘上各开一狭缝,两狭缝夹角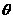 可调(如图16(b));右为水平放置的长为d的感光板,板的正上方有一匀强磁场,方向垂直纸面向外,磁感应强度为B.一小束速度不同、带正电的粒子沿水平方向射入N1,能通过N2的粒子经O点垂直进入磁场。
O到感光板的距离为
可调(如图16(b));右为水平放置的长为d的感光板,板的正上方有一匀强磁场,方向垂直纸面向外,磁感应强度为B.一小束速度不同、带正电的粒子沿水平方向射入N1,能通过N2的粒子经O点垂直进入磁场。
O到感光板的距离为 ,粒子电荷量为q,质量为m,不计重力。
,粒子电荷量为q,质量为m,不计重力。
(1)若两狭缝平行且盘静止(如图16(c)),某一粒子进入磁场后,竖直向下打在感光板中心点M上,求该粒子在磁场中运动的时间t;
(2)若两狭缝夹角为 ,盘匀速转动,转动方向如图16(b).要使穿过N1、N2的粒子均打到感光板P1P2连线上。试分析盘转动角速度
,盘匀速转动,转动方向如图16(b).要使穿过N1、N2的粒子均打到感光板P1P2连线上。试分析盘转动角速度 的取值范围(设通过N1的所有粒子在盘转一圈的时间内都能到达N2)。
的取值范围(设通过N1的所有粒子在盘转一圈的时间内都能到达N2)。
解:
(1)分析该粒子轨迹圆心为P1,半径为 ,在磁场中转过的圆心角为
,在磁场中转过的圆心角为 ,因而运动时间为:
,因而运动时间为: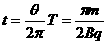
(2)设粒子从N1运动到N2过程历时为t,之后在磁场中运行速度大小为v,轨迹半径为R则:
在粒子匀速过程有:
L=vt ①
粒子出来进入磁场的条件:
 ②
②
在磁场中做匀速圆周运动有:
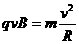 ③
③
设粒子刚好过P1点、P2点时轨迹半径分别为:R1、R2则:
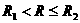 ④
④
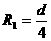 ⑤
⑤
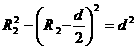 ⑥
⑥
由①-⑥得: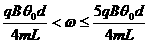
21、(福建卷)(19分)如图所示,两条平行的光滑金属导轨固定在倾角为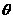 的绝缘斜面上,导轨上端连接一个定值电阻。导体棒a和b放在导轨上,与导轨垂直并良好接触。斜面上水平虚线PQ以下区域内,存在着垂直穿过斜面向上的匀强磁场。现对a棒施以平行导轨斜向上的拉力,使它沿导轨匀速向上运动,此时放在导轨下端的b棒恰好静止。当a棒运动到磁场的上边界PQ处时,撤去拉力,a棒将继续沿导轨向上运动一小段距离后再向下滑动,此时b棒已滑离导轨。当a棒再次滑回到磁场边界PQ处时,又恰能沿导轨匀速向下运动。已知a棒、b棒和定值电阻的阻值均为R,b棒的质量为m,重力加速度为g,导轨电阻不计。求
的绝缘斜面上,导轨上端连接一个定值电阻。导体棒a和b放在导轨上,与导轨垂直并良好接触。斜面上水平虚线PQ以下区域内,存在着垂直穿过斜面向上的匀强磁场。现对a棒施以平行导轨斜向上的拉力,使它沿导轨匀速向上运动,此时放在导轨下端的b棒恰好静止。当a棒运动到磁场的上边界PQ处时,撤去拉力,a棒将继续沿导轨向上运动一小段距离后再向下滑动,此时b棒已滑离导轨。当a棒再次滑回到磁场边界PQ处时,又恰能沿导轨匀速向下运动。已知a棒、b棒和定值电阻的阻值均为R,b棒的质量为m,重力加速度为g,导轨电阻不计。求
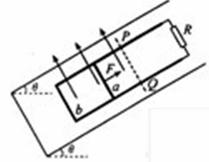
(1)a棒在磁场中沿导轨向上运动的过程中,a棒中的电流强度I,与定值电阻R中的电流强度IR之比;
(2)a棒质量ma;
(3)a棒在磁场中沿导轨向上运动时所受的拉力F。
解析:
(1)a棒沿导轨向上运动时,a棒、b棒及电阻R中的电流分别为Ia、Ib、IR,有
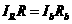
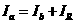
解得: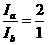
(2)由于a棒在PQ上方滑动过程中机械能守恒,因而a棒在磁场中向上滑动的速度大小v1与在磁场中向下滑动的速度大小v2相等,即v1=v2=v
设磁场的磁感应强度为B,导体棒长为L乙,a棒在磁场中运动时产生的感应电动势为
E=Blv
当a棒沿斜面向上运动时
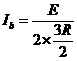
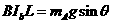
向下匀速运动时,a棒中的电流为Ia’、则
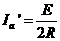
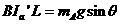
由以上各式联立解得: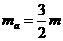
(3)由题可知导体棒a沿斜面向上运动时,所受拉力
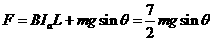
9.(江苏卷)如图所示,在匀强磁场中附加另一匀强磁场,附加磁场位于图中阴影区域,附加磁场区域的对称轴OO’与SS’垂直。a、b、c三个质子先后从S点沿垂直于磁场的方向摄入磁场,它们的速度大小相等,b的速度方向与SS’垂直,a、c的速度方向与b的速度方向间的夹角分别为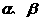 ,且
,且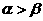 。三个质子经过附加磁场区域后能达到同一点S’,则下列说法中正确的有
。三个质子经过附加磁场区域后能达到同一点S’,则下列说法中正确的有

A.三个质子从S运动到S’的时间相等
B.三个质子在附加磁场以外区域运动时,运动轨迹的圆心均在OO’轴上
C.若撤去附加磁场,a到达SS’连线上的位置距S点最近
D.附加磁场方向与原磁场方向相同
答案:CD
解析:
A.三个质子从S运动到S’的时间不相等,A错误;
B.三个质子在附加磁场意外区域运动时,只有b运动轨迹的圆心在OO’轴上,因为半径相等,而圆心在初速度方向的垂线上,所以B错误;
C.用作图法可知,若撤去附加电场,a到达SS’连线上的位置距S点最近,b最远;C正确;
D.因b要增大曲率,才能使到达SS’连线上的位置向S点靠近,所以附加磁场方向与原磁场方向相同,D正确;
本体选CD。
本体考查带电粒子在磁场中的运动。
难度:难。
21.(重庆卷)如题21图所示,矩形MNPQ区域内有方向垂直于纸面的匀强磁场,有5个带电粒子从图中箭头所示位置垂直于磁场边界进入磁块,在纸面民内做匀速圆周运动,运动轨迹为相应的圆弧,这些粒子的质量,电荷量以及速度大小如下表所示
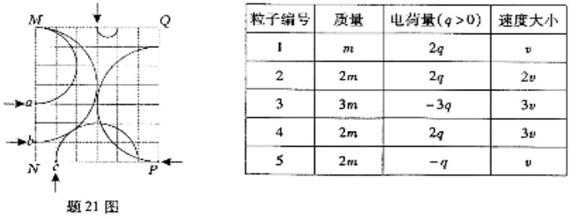
由以上信息可知,从图中a、b、c处进大的粒子对应表中的编号分别为
A 3、5、4 B4、 2、5
C5、3、2 D2、4、5
答案:D
[解析]根据半径公式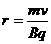 结合表格中数据可求得1-5各组粒子的半径之比依次为0.5︰2︰3︰3︰2,说明第一组正粒子的半径最小,该粒子从MQ边界进入磁场逆时针运动。由图a、b粒子进入磁场也是逆时针运动,则都为正电荷,而且a、b粒子的半径比为2︰3,则a一定是第2组粒子,b是第4组粒子。c顺时针运动,都为负电荷,半径与a相等是第5组粒子。正确答案D。
结合表格中数据可求得1-5各组粒子的半径之比依次为0.5︰2︰3︰3︰2,说明第一组正粒子的半径最小,该粒子从MQ边界进入磁场逆时针运动。由图a、b粒子进入磁场也是逆时针运动,则都为正电荷,而且a、b粒子的半径比为2︰3,则a一定是第2组粒子,b是第4组粒子。c顺时针运动,都为负电荷,半径与a相等是第5组粒子。正确答案D。
13.(上海物理) 如图,长为 的直导线拆成边长相等,夹角为
的直导线拆成边长相等,夹角为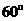 的
的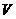 形,并置于与其所在平面相垂直的匀强磁场中,磁感应强度为
形,并置于与其所在平面相垂直的匀强磁场中,磁感应强度为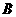 ,当在该导线中通以电流强度为
,当在该导线中通以电流强度为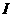 的电流时,该
的电流时,该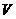 形通电导线受到的安培力大小为
形通电导线受到的安培力大小为

(A)0
(B)0.5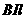 (C)
(C)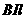 (D)
(D)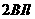
答案:C
解析:导线有效长度为2lsin30°=l,所以该V形通电导线收到的安培力大小为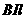 。选C。
。选C。
本题考查安培力大小的计算。
难度:易。
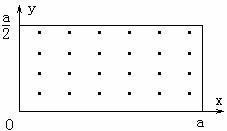
25.(新课标卷)(18分)如图所示,在0≤x≤a、o≤y≤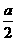 范围内有垂直于xy平面向外的匀强磁场,磁感应强度大小为B。坐标原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0-90°范围内.己知粒子在磁场中做圆周运动的半径介于
范围内有垂直于xy平面向外的匀强磁场,磁感应强度大小为B。坐标原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0-90°范围内.己知粒子在磁场中做圆周运动的半径介于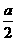 到a之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一,求最后离开磁场的粒子从粒子源射出时的:
到a之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一,求最后离开磁场的粒子从粒子源射出时的:
(1)速度大小;
(2)速度方向与y轴正方向夹角正弦。
解析:
设粒子的发射速度为v,粒子做圆周运动的轨道半径为R,由牛顿第二定律和洛伦磁力公式,得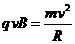 ,解得:
,解得:
当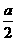 <R<a时,在磁场中运动时间最长的粒子,其轨迹是圆心为C的圆弧,圆弧与磁场的边界相切,如图所示,设该粒子在磁场中运动的时间为t,依题意,
<R<a时,在磁场中运动时间最长的粒子,其轨迹是圆心为C的圆弧,圆弧与磁场的边界相切,如图所示,设该粒子在磁场中运动的时间为t,依题意,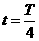 时,
时,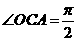
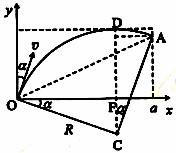
设最后离开磁场的粒子的发射方向与y轴正方向的夹角为α,由几何关系可得:
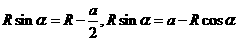 再加上
再加上 ,解得:
,解得:

(海南卷)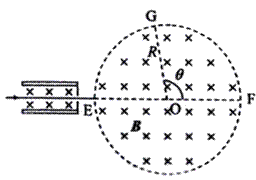 15.右图中左边有一对平行金属板,两板相距为d.电压为V;两板之间有匀强磁场,磁感应强度大小为
15.右图中左边有一对平行金属板,两板相距为d.电压为V;两板之间有匀强磁场,磁感应强度大小为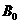 ,方向与金属板面平行并垂直于纸面朝里。图中右边有一半径为R、圆心为O的圆形区域内也存在匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。一电荷量为q的正离子沿平行于全属板面、垂直于磁场的方向射入平行金属板之间,沿同一方向射出平行金属板之间的区域,并沿直径EF方向射入磁场区域,最后从圆形区城边界上的G点射出.已知弧
,方向与金属板面平行并垂直于纸面朝里。图中右边有一半径为R、圆心为O的圆形区域内也存在匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。一电荷量为q的正离子沿平行于全属板面、垂直于磁场的方向射入平行金属板之间,沿同一方向射出平行金属板之间的区域,并沿直径EF方向射入磁场区域,最后从圆形区城边界上的G点射出.已知弧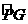 所对应的圆心角为
所对应的圆心角为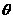 ,不计重力.求
,不计重力.求
(1)离子速度的大小;
(2)离子的质量.
答案:(1)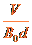 (2)
(2)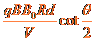
解析:(1)由题设知,离子在平行金属板之间做匀速直线运动,安所受到的向上的压力和向下的电场力平衡
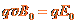 ①
①
式中,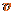 是离子运动速度的大小,
是离子运动速度的大小,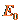 是平行金属板之间的匀强电场的强度,有
是平行金属板之间的匀强电场的强度,有
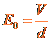 ②
②
由①②式得
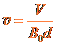 ③
③
(2)在圆形磁场区域,离子做匀速圆周运动,由洛伦兹力公式和牛顿第二定律有
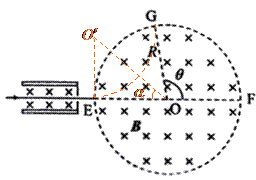
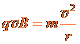 ④
④
式中,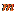 和
和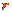 分别是离子的质量和它做圆周运动的半径。由题设,离子从磁场边界上的点G穿出,离子运动的圆周的圆心
分别是离子的质量和它做圆周运动的半径。由题设,离子从磁场边界上的点G穿出,离子运动的圆周的圆心 必在过E点垂直于EF的直线上,且在EG的垂直一平分线上(见右图)。由几何关系有
必在过E点垂直于EF的直线上,且在EG的垂直一平分线上(见右图)。由几何关系有
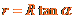 ⑤
⑤
式中,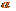 是
是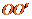 与直径EF的夹角,由几何关系得
与直径EF的夹角,由几何关系得
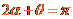 ⑥
⑥
联立③④⑤⑥式得,离子的质量为 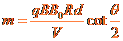 ⑦
⑦
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com