
题目列表(包括答案和解析)
3.

图1-2-5
(2009·江苏,7)如图1-2-5所示,以8 m/s匀速行驶的汽车即将通过路口,绿灯还有2 s将熄灭,此时汽车距离停车线18 m.该车加速时最大加速度大小为2 m/s2,减速时最大加速度大小为5 m/s2.此路段允许行驶的最大速度为12.5 m/s.下列说法中正确的有( )
A.如果立即做匀加速运动,在绿灯熄灭前汽车可能通过停车线
B.如果立即做匀加速运动,在绿灯熄灭前通过停车线汽车一定超速
C.如果立即做匀减速运动,在绿灯熄灭前汽车一定不能通过停车线
D.如果距停车线5 m处减速,汽车能停在停车线处
解析:在加速阶段若一直加速则2 s末的速度为12 m/s,2 s内的位移为x=×2 m=20 m,则在绿灯熄灭前汽车可能通过停车线,A正确.汽车一直减速在绿灯熄灭前通过的距离小于16 m,则不能通过停车线,如距离停车线5 m处减速,汽车运动的最小距离为6.4 m,不能停在停车线处.A、C正确.
答案:AC
2. 静止置于水平地面的一物体质量为m=57 kg,与水平地面间的动摩擦因数为0.43,在F=287 N的水平拉力作用下做匀变速直线运动,则由此可知物体在运动过程中第5个7秒内的位移与第11个3秒内的位移比为( )
A.2∶1 B.1∶2 C.7∶3 D.3∶7
解析:第5个7秒内的位移为x1=a×352-a×282,第11个3秒内的位移为x2=a×332-a×302,所以==.
答案:C
1. 一个小石块从空中a点自由落下,先后经过b点和c点,不计空气阻力.已知它经过b点时的速度为v,经过c点时的速度为3v,则ab段与ac段位移之比为( )
A.1∶3 B.1∶5 C.1∶8 D.1∶9
解析:经过b点时的位移为hab=,经过c点时的位移为hac=,所以hab∶hac=1∶9,故选D.
答案:D
12.
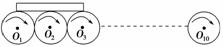
图5-3-31
10只相同的小圆轮并排水平紧密排列,圆心分别为O1、O2、O3、…、O10,已知O1O10=3.6 m,水平转轴通过圆心,圆轮绕轴顺时针转动的转速均为 r/s.现将一根长0.8 m、质量为2.0 kg的匀质木板平放在这些轮子的左端,木板左端恰好与O1竖直对齐,如图5-3-31所示,木板与轮缘间的动摩擦因数为0.16,不计轴与轮间的摩擦,g取10 m/s2.试求:
(1)轮缘的线速度大小;
(2)木板在轮子上水平移动的总时间;
(3)轮在传送木板过程中所消耗的机械能.
解析:(1)轮缘转动的线速度:v=2πnr=1.6 m/s.
(2)板运动的加速度:a=μg=0.16×10 m/s2=1.6 m/s2
板在轮上做匀加速运动的时间:t===1 s
板在做匀加速运动中所发生的位移:x1=at2=×1.6×12 m=0.8 m
板在做匀速运动的全过程中其重心平动发生的位移为:x2=3.6 m-0.8 m-0.4 m=2.4 m
因此,板运动的总时间为:t=t1+=1 s+ s=2.5 s.
(3)由功能关系知:轮子在传送木板的过程中所消耗的机械能一部分转化成了木板的动能,另一部分因克服摩擦力做功转化成了内能,即:
木板获得的动能:Ek=mv2,摩擦力做功产生的内能:Q=Ff·Δx
加速过程木板与轮子间的相对位移:Δs=v·t-·t,消耗的机械能:ΔE=Ek+Q
联立上述四个方程解得:ΔE=mv2=2×1.62 J=5.12 J.
答案:(1)1.6 m/s (2)2.5 s (3)5.12 J
11.

图5-3-30
如图5-3-30所示,AB为半径R=0.8 m的1/4光滑圆弧轨道,下端B恰与小车右端平滑对接.小车质量M=3 kg,车长L=2.06 m,车上表面距地面的高度h=0.2 m.现有一质量m=1 kg的滑块,由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5 s时,车被地面装置锁定.(g=10 m/s2)试求:
(1)滑块到达B端时,轨道对它支持力的大小;
(2)车被锁定时,车右端距轨道B端的距离;
(3)从车开始运动到被锁定的过程中,滑块与车面间由于摩擦而产生的内能大小;
(4)滑块落地点离车左端的水平距离.
解析:(1)设滑块到达B端时速度为v,
由动能定理,得mgR=mv2
由牛顿第二定律,得FN-mg=m
联立两式,代入数值得轨道对滑块的支持力:FN=3mg=30 N.
(2)当滑块滑上小车后,由牛顿第二定律,得
对滑块有:-μmg=ma1
对小车有:μmg=Ma2
设经时间t两者达到共同速度,则有:v+a1t=a2t
解得t=1 s.由于1 s<1.5 s,此时小车还未被锁定,两者的共同速度:v′=a2t=1 m/s
因此,车被锁定时,车右端距轨道B端的距离:x=a2t2+v′t′=1 m.
(3)从车开始运动到被锁定的过程中,滑块相对小车滑动的距离Δx=t-a2t2=2 m
所以产生的内能:E=μmgΔx=6 J.
(4)对滑块由动能定理,得-μmg(L-Δx)=mv″2-mv′2
滑块脱离小车后,在竖直方向有:h=gt″2
所以,滑块落地点离车左端的水平距离:x′=v″t″=0.16 m.
答案:(1)30 N (2)1 m (3)6 J (4)0.16 m
10.

图5-3-29
(2010·泰州市联考)如图5-3-29所示,半径为R的竖直光滑圆轨道内侧底部静止着一个光滑小球,现给小球一个冲击使其在瞬间得到一个水平初速度v0,若v0大小不同,则小球能够上升到的最大高度(距离底部)也不同.下列说法中正确的是( )
A.如果v0=,则小球能够上升的最大高度为
B.如果v0=,则小球能够上升的最大高度为
C.如果v0=,则小球能够上升的最大高度为
D.如果v0=,则小球能够上升的最大高度为2R
解析:根据机械能守恒定律,当速度为v0=,由mgh=mv解出h=,A项正确,B项错误;当v0=,小球正好运动到最高点,D项正确;当v0=时小球运动到最高点以下,若C项成立,说明小球此时向心力为0,这是不可能的.
答案:AD
9.
图5-3-28
在2008北京奥运会上,俄罗斯著名撑杆跳运动员伊辛巴耶娃以5.05 m的成绩第24次打破世界记录.图5-3-28为她在比赛中的几个画面,下列说法中正确的是( )
A.运动员过最高点时的速度为零
B.撑杆恢复形变时,弹性势能完全转化为动能
C.运动员要成功跃过横杆,其重心必须高于横杆
D.运动员在上升过程中对杆先做正功后做负功
解析:撑杆跳运动员过最高点时竖直速度为零,水平速度不为零,选项A错误;当运动员到达最高点杆恢复形变时,弹性势能转化为运动员的重力势能和动能,选项B错误;运动员可以背跃式跃过横杆,其重心可能低于横杆,选项C错误;运动员在上升过程中对杆先做正功转化为杆的弹性势能后做负功,杆的弹性势能转化为运动员的重力势能和动能,选项D正确.
答案:D
8.
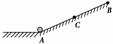
图5-3-27
如图5-3-27所示,小球从A点以初速度v0沿粗糙斜面向上运动,到达最高点B后返回A,C为AB的中点.下列说法中正确的是( )
A.小球从A出发到返回A的过程中,位移为零,合外力做功为零
B.小球从A到C过程与从C到B过程,减少的动能相等
C.小球从A到B过程与从B到A过程,损失的机械能相等
D.小球从A到C过程与从C到B过程,速度的变化量相等
解析:小球从A出发到返回A的过程中,位移为零,重力做功为零,支持力不做功,摩擦力做负功,所以A选项错误;从A到B的过程与从B到A的过程中,位移大小相等,方向相反,损失的机械能等于克服摩擦力做的功,所以C选项正确;小球从A到C过程与从C到B过程,位移相等,合外力也相等,方向与运动方向相反,所以合外力做负功,大小相等,所以减少的动能相等,因此,B选项正确;小球从A到C过程与从C到B过程中,减少的动能相等,而动能的大小与质量成正比,与速度的平方成正比,所以D错误.
答案:BC
7.

图5-3-26
来自福建省体操队的运动员黄珊汕是第一位在奥运会上获得蹦床奖牌的中国选手.蹦床是一项好看又惊险的运动,如图5-3-26所示为运动员在蹦床运动中完成某个动作的示意图,图中虚线PQ是弹性蹦床的原始位置,A为运动员抵达的最高点,B为运动员刚抵达蹦床时的位置,C为运动员抵达的最低点.不考虑空气阻力和运动员与蹦床作用时的机械能损失,A、B、C三个位置运动员的速度分别是vA、vB、vC,机械能分别是EA、EB、EC,则它们的大小关系是( )
A.vA<vB,vB>vC B.vA>vB,vB<vC
C.EA=EB,EB>EC D.EA>EB,EB=EC
A机械能守恒,EA=EB,B→A机械能守恒,EA=EB,B→C弹力对人做负功,机械能减小,EB>EC.
答案:AC
6.
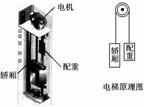
图5-3-25
如图5-3-25所示,电梯由质量为1×103 kg的轿厢、质量为8×102 kg的配重、定滑轮和钢缆组成,轿厢和配重分别系在一根绕过定滑轮的钢缆两端,在与定滑轮同轴的电动机驱动下电梯正常工作,定滑轮与钢缆的质量可忽略不计,重力加速度g=10 m/s2.在轿厢由静止开始以2 m/s2的加速度向上运行1 s的过程中,电动机对电梯共做功为( )
A.2.4×103 J B.5.6×103 J
C.1.84×104 J D.2.16×104 J
解析:电动机做功:W=(M-m)gh+(M+m)v2=(1 000-800)×10×1+(1 000+800)×22=5 600 J.
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com