11.

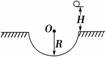
图5－2－18

如图5－2－18所示，质量m＝0.5 kg的小球从距离地面高H＝5 m处自由下落，到达地面时恰能沿凹陷于地面的半圆形槽壁运动，半圆形槽的半径R＝0.4 m，小球到达槽最低点时速率恰好为10 m/s，并继续沿槽壁运动直到从槽左端边缘飞出且沿竖直方向上升、下落，如此反复几次，设摩擦力大小恒定不变，取g＝10 m/s²，求：

(1)小球第一次飞出半圆形槽上升到距水平地面的高度h为多少？

(2)小球最多能飞出槽外几次？

解析：(1)在小球下落到最低点的过程中，设小球克服摩擦力做功为W_f，由动能定理得：

mg(H+R)－W_f＝mv²－0

从小球下落到第一次飞出半圆形槽上升到距水平地面h高度的过程中，

由动能定理得mg(H－h)－2W_f＝0－0

联立解得：h＝－H－2R＝ m－5 m－2×0.4 m＝4.2 m.

(2)设小球最多能飞出槽外n次，则由动能定理得：mgH－2nW_f＝0－0

解得：n＝＝＝＝6.25

故小球最多能飞出槽外6次．

答案：(1)4.2 m　(2)6次

10．在2008年四川汶川大地震抗震救灾活动中，为转移被困群众动用了直升飞机．设被救人员的质量m＝80 kg，所用吊绳的拉力最大值F_m＝1 200 N，所用电动机的最大输出功率为P_m＝12 kW，为尽快吊起被困群众，操作人员采取的办法是，先让吊绳以最大的拉力工作一段时间，而后电动机又以最大功率工作，被救人员上升h＝90 m时恰好达到最大速度(g取10 m/s²)，试求：

(1)被救人员刚到达机舱时的速度；

(2)这一过程所用的时间．

解析：(1)第一阶段绳以最大拉力拉着被救人员匀加速上升，当电动机达到最大功率时，功率保持不变，被救人员变加速上升，速度增大，拉力减小，当拉力与重力相等时速度达到最大．由P_m＝F_Tv_m＝mgv_m得v_m＝＝ m/s＝15 m/s

(2)a₁＝＝ m/s²＝5 m/s²

匀加速阶段的末速度v₁＝＝ m/s＝10 m/s，时间t₁＝＝ s＝2 s

上升的高度h₁＝t₁＝×2 m＝10 m

对于以最大功率上升过程，由动能定理得：P_mt₂－mg(h－h₁)＝mv－mv

代入数据解得t₂＝5.75 s，所以此过程所用总时间为t＝t₁+t₂＝(2+5.75) s＝7.75 s.

答案：(1)15 m/s　(2)7.75 s

9.

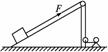
图5－2－17

如图5－2－17，卷扬机的绳索通过定滑轮用力F拉位于粗糙斜面上的木箱，使之沿斜面加速向上移动．在移动过程中，下列说法正确的是(　)

A．F对木箱做的功等于木箱增加的动能与木箱克服摩擦力所做的功之和

B．F对木箱做的功等于木箱克服摩擦力和克服重力所做的功之和

C．木箱克服重力做的功等于木箱增加的重力势能

D．F对木箱做的功等于木箱增加的机械能与木箱克服摩擦力做的功之和

解析：木箱加速上滑的过程中，拉力F做正功，重力和摩擦力做负功．支持力不做功，由动能定理得：W_F－W_G－W_f＝mv²－0.即W_F＝W_G+W_f+mv².A、B错误，又因克服重力做功W_G等于物体重力势能的增加，所以W_F＝ΔE_p+ΔE_k+W_f，故D正确，又由重力做功与重力势能变化的关系知C也正确．

答案：CD

8.

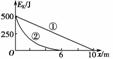
图5－2－16

构建和谐型、节约型社会深得民心，遍布于生活的方方面面．自动充电式电动车就是很好的一例，电动车的前轮装有发电机，发电机与蓄电池连接．当在骑车者用力蹬车或电动自行车自动滑行时，自行车就可以连通发电机向蓄电池充电，将其他形式的能转化成电能储存起来．现有某人骑车以500 J的初动能在粗糙的水平路面上滑行，第一次关闭自充电装置，让车自由滑行，其动能随位移变化关系如图5－2－16①所示；第二次启动自充电装置，其动能随位移变化关系如图线②所示，则第二次向蓄电池所充的电能是(　)

A．200 J　 　　　 B．250 J　 　 　C．300 J　 　　 　　D．500 J

解析：设自行车与路面的摩擦阻力为F_f，由图可知，关闭自动充电装置时，由动能定理得：0－Ek₀＝－F_f·x₁，可得F_f＝50 N，启动自充电装置后，自行车向前滑行时用于克服摩擦做功为：W＝F_fx₂＝300 J，设克服电磁阻力做功为W′，由动能定理得：－W′－W＝0－Ek₀，可得W′＝200 J.

答案：A

7.

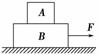
图5－2－15

如图5－2－15所示，一块长木板B放在光滑的水平面上，在B上放一物体A，现以恒定的外力拉B，由于A，B间摩擦力的作用，A将在B上滑动，以地面为参考系，A和B都向前移动一段距离，在此过程中(　)

A．外力F做的功等于A和B动能的增量

B．B对A的摩擦力所做的功等于A的动能的增量

C．A对B的摩擦力所做的功等于B对A的摩擦力所做的功

D．外力F对B做的功等于B的动能的增量与B克服摩擦力所做的功之和

解析：A物体所受的合外力等于B对A的摩擦力，对A物体运用动能定理，则有B对A的摩擦力所做的功，等于A的动能的增量，即B对．A对B的摩擦力与B对A的摩擦力是一对作用力与反作用力，大小相等，方向相反，但是由于A在B上滑动，A，B对地的位移不等，故二者做功不等，C错．对B物体应用动能定理，W_F－W_f＝ΔEk_B，即W_F＝ΔEk_B+W_f，就是外力F对B做的功等于B的动能增量与B克服摩擦力所做的功之和，D对．由前述讨论知B克服摩擦力所做的功与A的动能增量(等于B对A的摩擦力所做的功)不等，故A错．

答案：BD

6.

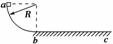
图5－2－14

如图5－2－14所示，在光滑四分之一圆弧轨道的顶端a点，质量为m的物块(可视为质点)由静止开始下滑，经圆弧最低点b滑上粗糙水平面，圆弧轨道在b点与水平轨道平滑相接，物块最终滑至c点停止．若圆弧轨道半径为R，物块与水平面间的动摩擦因数为μ，下列说法正确的是(　)

A．物块滑到b点时的速度为　 　　　 B．物块滑到b点时对b点的压力是3mg

C．c点与b点的距离为　 　　　　 D．整个过程中物块机械能损失了mgR

解析：物块滑到b点时，mgR＝mv²－0，v＝，A不正确．在b点，F_N－mg＝m，F_N＝3mg，B正确．从a点到c点，机械能损失了mgR，D正确．mgR－μmgs＝0－0，s＝，C正确．

答案：BCD

5.

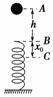
图5－2－13

如图5－2－13所示，一轻弹簧直立于水平地面上，质量为m的小球从距离弹簧上端B点h高处的A点自由下落，在C点处小球速度达到最大．x₀表示B、C两点之间的距离；E_k表示小球在C处的动能．若改变高度h，则下列表示x₀随h变化的图象和E_k随h变化的图象中正确的是(　)

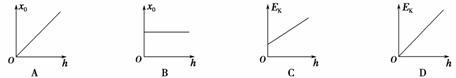
解析：由题意“在C点处小球速度达到最大”，可知C点是平衡位置，小球受到的重力与弹力平衡，该位置与h无关，B项正确；根据动能定理有mg(h+x₀)－E_p＝mv＝E_k，其中x₀与弹性势能E_p为常数，可判断出C项正确．

答案：BC

4．小球由地面竖直上抛，上升的最大高度为H，设所受阻力大小恒定，地面为零势能面．在上升至离地高度h处，小球的动能是势能的2倍，在下落至离地高度h处，小球的势能是动能的2倍，则h等于(　)

A.　 　　　　 B. 　 　　C.　 　　　 D.

解析：设小球上升离地高度h时，速度为v₁，地面上抛时速度为v₀，下落至离地面高度h处速度为v₂，设空气阻力为f

上升阶段：－mgH－fH＝－mv，－mgh－fh＝mv－mv

又2mgh＝mv

下降阶段：mg(H－h)－f(H－h)＝mv，mgh＝2×mv

由上式联立得：h＝H.

答案：D

3．(2010·江门模拟)起重机将物体由静止举高h时，物体的速度为v，下列各种说法中正确的是(不计空气阻力)(　)

A．拉力对物体所做的功，等于物体动能和势能的增量

B．拉力对物体所做的功，等于物体动能的增量

C．拉力对物体所做的功，等于物体势能的增量

D．物体克服重力所做的功，大于物体势能的增量

解析：根据动能定理W_F－W_G＝mv²/2，W_G＝mgh，所以W_F＝mv²/2+mgh，A正确，B、C错误；物体克服重力所做的功，等于物体重力势能的增量，D错误．

答案：A

2．一个木块静止于光滑水平面上，现有一个水平飞来的子弹射入此木块并深入2 cm而相对于木块静止，同时间内木块被带动前移了1 cm，则子弹损失的动能、木块获得动能以及子弹和木块共同损失的动能三者之比为(　)

A．3∶1∶2　 　　 B．3∶2∶1 　　 C．2∶1∶3　 　　 D．2∶3∶1

解析：设子弹深入木块深度为d，木块移动s，则子弹对地位移为d+s；设子弹与木块的相互作用力为f，由动能定理，子弹损失的动能等于子弹克服木块阻力所做的功，即ΔE₁＝f(d+s)，木块所获得的动能等于子弹对木块作用力所做的功，即ΔE₂＝fs，子弹和木块共同损失的动能为ΔE₃＝ΔE₁－ΔE₂＝fd，即三者之比为(d+s)∶s∶d＝3∶1∶2.

答案：A