11.

图3－2－19

如图3－2－19所示，长L＝1.5 m，高h＝0.45 m，质量M＝10 kg的长方体木箱，在水平面上向右做直线运动．当木箱的速度v₀＝3.6 m/s时，对木箱施加一个方向水平向左的恒力F＝50 N，并同时将一个质量m＝1 kg的小球轻放在距木箱右端的P点(小球可视为质点，放在P点时相对于地面的速度为零)，经过一段时间，小球脱离木箱落到地面．木箱与地面的动摩擦因数为0.2，其他摩擦均不计．取g＝10 m/s².求：

(1)小球从离开木箱开始至落到地面所用的时间；

(2)小球放在P点后，木箱向右运动的最大位移；

(3)小球离开木箱时木箱的速度．

解析：(1)小球从离开木箱开始至落到地面所用的时间

由h＝gt²，t＝ ＝ s＝0.3 s.

(2)小球放到木箱上后相对地面静止，木箱的加速度为

a₁＝＝ m/s²＝7.2 m/s²

木箱向右运动的最大位移为：x₁＝＝ m＝0.9 m.

(3)x₁小于1 m，所以小球不会从木箱的左端掉下．

木箱向左运动的加速度为a₂＝＝ m/s²＝2.8 m/s²

设木箱向左运动的距离为x₂时，小球脱离木箱x₂＝x₁+＝0.9 m+0.5 m＝1.4 m

设木箱向左运动的时间为t₂，由x＝at²得t₂＝ ＝ s＝1 s

小球刚离开木箱瞬间，木箱的速度方向向左，大小为v₂＝a₂t₂＝2.8×1 m/s＝2.8 m/s.

答案：(1)0.3 s　(2)0.9 m　(3)2.8 m/s

10.

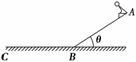
图3－2－18

如图3－2－18为一滑梯的示意图，滑梯的长度AB为L＝5.0 m，倾角θ＝37°.BC段为与滑梯平滑连接的水平地面．一个小孩从滑梯顶端由静止开始滑下，离开B点后在地面上滑行了s＝2.25 m后停下．小孩与滑梯间的动摩擦因数为μ＝0.3.不计空气阻力．取g＝10 m/s².已知sin 37°＝0.6，cos 37°＝0.8.求：

(1)小孩沿滑梯下滑时的加速度a的大小；

(2)小孩滑到滑梯底端B时的速度v的大小；

(3)小孩与地面间的动摩擦因数μ′.

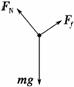
解析：(1)小孩受力如右图所示

由牛顿运动定律得mgsin θ－μF_N＝ma，F_N－mgcos　 θ＝0

解得a＝gsin θ－μgcos θ＝3.6 m/s².

(2)由v²＝2aL，求出v＝6 m/s.

(3)由匀变速直线运动规律得0－v²＝2a′s，由牛顿第二定律得μ′mg＝ma′，解得μ′＝0.8.

答案：(1)3.6 m/s²　(2)6 m/s　(3)0.8

9.

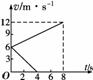
图3－2－17

两个完全相同的物块A、B，质量均为m＝0.8 kg，在同一粗糙水平面上以相同的初速度从同一位置开始运动．图3－2－17中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v－t图象，求：

(1)物块A所受拉力F的大小；

(2)8 s末物块A、B之间的距离x.

解析：(1)设A、B两物块的加速度分别为a₁、a₂，

由v－t图象可得：

a₁＝＝ m/s²＝0.75 m/s²①

a₂＝＝ m/s²＝－1.5 m/s²

负号表示加速度方向与初速度方向相反．②

对A、B两物块分别由牛顿第二定律得：

F－F_f＝ma₁③

－F_f＝ma₂④

由①-④式可得：F＝1.8 N.

(2)设A、B两物块8 s内的位移分别为x₁、x₂由图象得：

x₁＝×(6+12)×8＝72 m，x₂＝×6×4＝12 m，所以x＝x₁－x₂＝60 m.

答案：(1)1.8 N　(2)60 m

8.

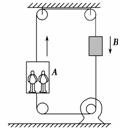
图3－2－16

如图3－2－16是一种升降电梯的示意图，A为载人箱，B为平衡重物，它们的质量均为M，上下均由跨过滑轮的钢索系住，在电动机的牵引下使电梯上下运动．如果电梯中人的总质量为m，匀速上升的速度为v，电梯即将到顶层前关闭电动机，依靠惯性上升h高度后停止，在不计空气和摩擦阻力的情况下，h为(　)

A.　 　　　　　 　　B.

C.　 　　 　　D.

解析：关闭电动机后，载人箱A受到B对A的向上的拉力为Mg，A及人的总重力为(M+m)g，载人箱A加速度大小为a＝＝g，

由2ah＝v²得h＝，选项B正确．

设B对A拉力F_T

对B：F_T－Mg＝Ma

对A：F_T－(M+m)g＝(M+m)a，a＝

由V²＝2ah得h＝，D选项正确．

答案：BD

7．

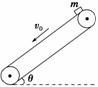
图3－2－15

(2010·潍坊高三教学质量检测)如图3－2－15所示，足够长的传送带与水平面夹角为θ，以速度v₀逆时针匀速转动．在传送带的上端轻轻放置一个质量为m的小木块，小木块与传送带间的动摩擦因数μ＜tan θ，则图3－2－15中能客观地反映小木块的速度随时间变化关系的是(　)

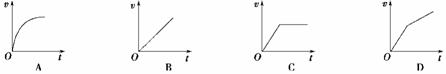
解析：对m开始时加速度a₁＝μgcos θ+gsin θ.达到共同速度时，物体的摩擦力方向由沿斜面向下变为沿斜面向上．以后物体运动的加速度a₂＝gsin θ－μgcos θ，显然a₁>a₂，只有图象D正确．

答案：D

6.

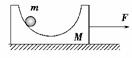
图3－2－14

质量为M的光滑圆槽放在光滑水平面上，一水平恒力F作用在其上促使质量为m的小球静止在圆槽上，如图3－2－14所示，则(　)

A．小球对圆槽的压力为

B．小球对圆槽的压力为

C．水平恒力F变大后，如果小球仍静止在圆槽上，小球对圆槽的压力增加

D．水平恒力F变大后，如果小球仍静止在圆槽上，小球对圆槽的压力减小

解析：利用整体法可求得系统的加速度为a＝，对小球利用牛顿第二定律可得：小球对圆槽的压力为 ，可知只有C选项正确．

答案：C

5.

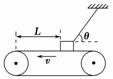
图3－2－13

如图3－2－13所示，质量为m的物体用细绳拴住放在水平粗糙传送带上，物体距传送带左端的距离为L，稳定时绳与水平方向的夹角为θ，当传送带分别以v₁、v₂的速度作逆时针转动时(v₁＜v₂)，绳中的拉力分别为F₁、F₂；若剪断细绳时，物体到达左端的时间分别为t₁、t₂，则下列说法正确的是(　)

A．F₁＜F₂　 　　　　　 B．F₁＝F₂

C．t₁一定大于t₂　 　　 D．t₁可能等于t₂

解析：皮带以不同的速度运动，物体所受的滑动摩擦力相等，物体仍处于静止状态，故F₁＝F₂.物体在两种不同速度下运动时有可能先加速再匀速，也可能一直加速，故t₁可能等于t₂.

答案：BD

4．质量为1吨的汽车在平直公路上以10 m/s的速度匀速行驶，阻力大小不变．从某时刻开始，汽车牵引力减少2 000 N，那么从该时刻起经过6 s，汽车行驶的路程是(　)

A．50 m　 　　　B．42 m　 　　C．25 m　 　　D．24 m

答案：C

3.

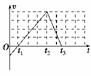
图3－2－12

2008北京奥运会取得了举世瞩目的成功，某运动员(可看作质点)参加跳板跳水比赛，t＝0是其向上起跳瞬间，其速度与时间关系图象如图3－2－12所示，则(　)

A．t₁时刻开始进入水面　 　 　B．t₂时刻开始进入水面

C．t₃时刻已浮出水面　 　　 　D．0-t₂的时间内，运动员处于失重状态

解析：跳水运动员离开跳板向上跳起，做减速运动，到达最高点后，开始向下做匀加速运动，直到刚进入水面，速度达到最大，进入水面后，又受到水的阻力，开始做减速运动，直至速度减小到零，根据图象可知，t₂时刻速度最大，所以t₂时刻开始进入水面，故A项错误，B项正确；t₃时刻速度为零，是在水中减速结束的时刻，故C项错误；跳水运动员离开跳板到刚开始进入水中时，都是只受重力，加速度等于重力加速度，方向向下，处于失重状态，故D项正确．

答案：BD

2.

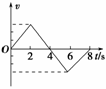
图3－2－11

某物体做直线运动的v－t图象如图3－2－11所示，据此判断下图(F表示物体所受合力，x表示物体的位移)四个选项中正确的是(　)

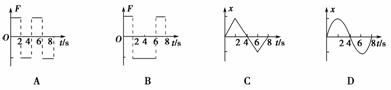
解析：从v－t图象中可以看出，物体在0-2 s内做初速度为零的匀加速运动，合力与速度方向一致且为恒力，在2 s-6 s内加速度方向与前2 s内速度方向相反，合外力方向与前2 s内速度方向相反，故A错误、B正确；由于加速度a恒定，所以匀加速运动范围内位移x与时间是二次函数关系，且4 s末的位移不为0，故C、D项错．

答案：B