7.

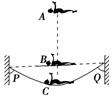
图5－3－26

来自福建省体操队的运动员黄珊汕是第一位在奥运会上获得蹦床奖牌的中国选手．蹦床是一项好看又惊险的运动，如图5－3－26所示为运动员在蹦床运动中完成某个动作的示意图，图中虚线PQ是弹性蹦床的原始位置，A为运动员抵达的最高点，B为运动员刚抵达蹦床时的位置，C为运动员抵达的最低点．不考虑空气阻力和运动员与蹦床作用时的机械能损失，A、B、C三个位置运动员的速度分别是v_A、v_B、v_C，机械能分别是E_A、E_B、E_C，则它们的大小关系是(　)

A．v_A<v_B，v_B>v_C　 　　　　　　　　　 　B．v_A>v_B，v_B<v_C

C．E_A＝E_B，E_B>E_C 　　　　　　　　　 　D．E_A>E_B，E_B＝E_C

A机械能守恒，E_A＝E_B，B→A机械能守恒，E_A＝E_B，B→C弹力对人做负功，机械能减小，E_B>E_C.

答案：AC

6.

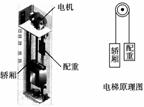
图5－3－25

如图5－3－25所示，电梯由质量为1×10³ kg的轿厢、质量为8×10² kg的配重、定滑轮和钢缆组成，轿厢和配重分别系在一根绕过定滑轮的钢缆两端，在与定滑轮同轴的电动机驱动下电梯正常工作，定滑轮与钢缆的质量可忽略不计，重力加速度g＝10 m/s².在轿厢由静止开始以2 m/s²的加速度向上运行1 s的过程中，电动机对电梯共做功为(　)

A．2.4×10³ J　 　　　　　　　　　 B．5.6×10³ J

C．1.84×10⁴ J　 　　　　　　　　 D．2.16×10⁴ J

解析：电动机做功：W＝(M－m)gh+(M+m)v²＝(1 000－800)×10×1+(1 000+800)×2²＝5 600 J.

答案：B

5.

图5－3－24

如图5－3－24所示，在动摩擦因数为0.2的水平面上有一质量为3 kg的物体被一个劲度系数为120 N/m的压缩轻质弹簧突然弹开，物体离开弹簧后在水平面上继续滑行了1.3 m才停下来，下列说法正确的是(g取10 m/s²)(　)

A．物体开始运动时弹簧的弹性势能E_p＝7.8 J

B．物体的最大动能为7.8 J

C．当弹簧恢复原长时物体的速度最大

D．当物体速度最大时弹簧的压缩量为x＝0.05 m

解析：物体离开弹簧后的动能设为E_k，由功能关系可得：E_k＝μmgx₁＝7.8 J，设弹簧开始的压缩量为x₀，则弹簧开始的弹性势能Ep₀＝μmg(x₀+x₁)＝7.8 J+μmgx₀＞7.8 J，A错误；当弹簧的弹力kx₂＝μmg时，物体的速度最大，得x₂＝0.05 m，D正确，C错误；物体在x₂＝0.05 m到弹簧的压缩量x₂＝0的过程做减速运动，故最大动能一定大于7.8 J，故B错误．

答案：D

4.

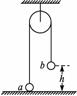
图5－3－23

如图5－3－23所示，一很长的、不可伸长的柔软轻绳跨过光滑定滑轮，绳两端各系一小球a和b.a球质量为m，静置于地面；b球质量为3m，用手托住，高度为h，此时轻绳刚好拉紧．从静止开始释放b后，a可能达到的最大高度为(　)

A．h　 　　　　　 B．1.5h　 　　　　　　 C．2h　 　　　　 　D．2.5h

解析：考查机械能守恒定律．在b球落地前，a、b球组成的系统机械能守恒，且a、b两球速度大小相等，根据机械能守恒定律可知：3mgh－mgh＝(m+3m)v²，v＝，b球落地时，a球高度为h，之后a球向上做竖直上抛运动，在这个过程中机械能守恒，mv²＝mgΔh，Δh＝＝，所以a球可能达到的最大高度为1.5h，B项正确．

答案：B

3.

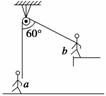
图5－3－22

如图5－3－22所示，一根跨越光滑定滑轮的轻绳，两端各有一杂技演员(可视为质点)，演员a站于地面，演员b从图示的位置由静止开始向下摆，运动过程中绳始终处于伸直状态，当演员b摆至最低点时，演员a刚好对地面无压力，则演员a与演员b质量之比为(　)

A．1∶1　 　　 B．2∶1 　　 C．3∶1　 　　 D．4∶1

解析：由机械能守恒定律求出演员b下落至最低点时的速度大小为v. mv²＝mgl(1－cos 60°)，v²＝2gl(1－cos 60°)＝gl.此时绳的拉力为T＝mg+m＝2mg，演员a刚好对地压力为0.则m_ag＝T＝2mg.故m_a∶m＝2∶1.

答案：B

2.

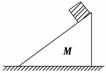
图5－3－21

如图5－3－21所示，斜面置于光滑水平地面上，其光滑斜面上有一物体由静止下滑，在物体下滑过程中，下列说法正确的是(　)

A．物体的重力势能减少，动能增加

B．斜面的机械能不变

C．斜面对物体的作用力垂直于接触面，不对物体做功

D．物体和斜面组成的系统机械能守恒

解析：物体下滑过程中，由于物体与斜面相互间有垂直于斜面的作用力，使斜面加速运动，斜面的动能增加；物体沿斜面下滑时，既沿斜面向下运动，又随斜面向右运动，其合速度方向与弹力方向不垂直，且夹角大于90°，所以物体克服相互作用力做功，物体的机械能减少，但动能增加，重力势能减少，故A项正确，B、C项错误．对物体与斜面组成的系统内，只有动能和重力势能之间的转化，故系统机械能守恒，D项正确．

答案：AD

1.

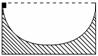
图5－3－20

如图5－3－20所示，一个质量为m的小铁块沿半径为R的固定半圆轨道上边缘由静止滑下，到半圆底部时，轨道所受压力为铁块重力的1.5倍，则此过程中铁块损失的机械能为(　)

A.mgR　 　　　 B.mgR　 　　　 C.mgR　 　　　 D.mgR

解析：设铁块在圆轨道底部的速度为v，则1.5mg－mg＝m，由能量守恒有：mgR－ΔE＝mv²，所以ΔE＝mgR.

答案：D

5.

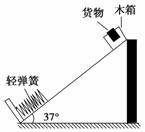
图5－3－19

(2010·成都市摸底测试)如图5－3－19所示为某同学设计的节能运输系统．斜面轨道的倾角为37°，木箱与轨道之间的动摩擦因数μ＝0.25.设计要求：木箱在轨道顶端时，自动装货装置将质量m＝2 kg的货物装入木箱，木箱载着货物沿轨道无初速滑下，当轻弹簧被压缩至最短时，自动装货装置立刻将货物御下，然后木箱恰好被弹回到轨道顶端，接着再重复上述过程．若g取10 m/s²，sin 37°＝0.6，cos 37°＝0.8.求：

(1)离开弹簧后，木箱沿轨道上滑的过程中的加速度大小；

(2)满足设计要求的木箱质量．

解析：(1)设木箱质量为m′，对木箱的上滑过程，由牛顿第二定律有：

m′gsin 37°+μm′gcos 37°＝m′a

代入数据解得：a＝8 m/s².

(2)设木箱沿轨道下滑的最大距离为L，弹簧被压缩至最短时的弹性势能为E_p，根据能量守恒定律：货物和木箱下滑过程中有：(m′+m)gsin 37°L＝μ(m′+m)gcos 37°L+E_p

木箱上滑过程中有E_p＝m′gsin 37°L+μm′gcos 37°L

联立代入数据解得：m′＝m＝2 kg.

答案：(1)8 m/s²　(2)2 kg

4．

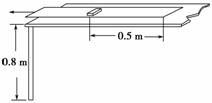
图5－3－18

如图5－3－18所示，静止放在水平桌面上的纸带，其上有一质量为m＝0.1 kg的铁块，它与纸带右端的距离为L＝0.5 m，铁块与纸带间、纸带与桌面间动摩擦因数均为μ＝0.1.现用力F水平向左将纸带从铁块下抽出，当纸带全部抽出时铁块恰好到达桌面边缘，铁块抛出后落地点离抛出点的水平距离为s＝0.8 m．已知g＝10 m/s²，桌面高度为H＝0.8 m，不计纸带质量，不计铁块大小，铁块不滚动．求：

(1)铁块抛出时速度大小；

(2)纸带从铁块下抽出所用时间t₁；

(3)纸带抽出过程产生的内能E.

解析：(1)水平方向：s＝vt①

竖直方向：H＝gt²②

由①②联立解得：v＝2 m/s.

(2)设铁块的加速度为a₁，由牛顿第二定律，得μmg＝ma₁③

纸带抽出时，铁块的速度v＝a₁t₁④

③④联立解得t₁＝2 s.

(3)铁块的位移s₁＝a₁t⑤

设纸带的位移为s₂；由题意知，s₂－s₁＝L⑥

由功能关系可得E＝μmgs₂+μmg(s₂－s₁)⑦

由③④⑤⑥⑦联立解得E＝0.3 J.

答案：(1)2 m/s　(2)2 s　(3)0.3 J

3.

图5－3－17

在奥运比赛项目中，高台跳水是我国运动员的强项．质量为m的跳水运动员进入水中后受到水的阻力而做减速运动，设水对他的阻力大小恒为F，那么在他减速下降高度为h的过程中，下列说法正确的是(g为当地的重力加速度)(　)

A．他的动能减少了Fh　 　　　　　　　　　　　 B．他的重力势能增加了mgh

C．他的机械能减少了(F－mg)h　 　　　　 D．他的机械能减少了Fh

解析：由动能定理，ΔE_k＝mgh－Fh，动能减少了Fh－mgh，A选项不正确；他的重力势能减少了mgh，B选项错误；他的机械能减少了ΔE＝Fh，C选项错误，D选项正确．

答案：D