3．如图8－4－16所示．有一混合正离子束先后通过正交电场、磁场区域Ⅰ和匀强磁场区域Ⅱ，如果这束正离子束在区域Ⅰ中不偏转，进入区域Ⅱ后偏转半径又相同，则说明这些正离子具有相同的(　)

　 A．速度　　 B．质量　　 C．电荷　　 D．比荷

　 解析：设电场的场强为E，由于粒子在区域Ⅰ里不发生偏转，则Eq＝B₁qv，得v＝；当粒子进入区域Ⅱ时，偏转半径又相同，所以R＝＝＝，故选项A、D正确．

　 答案：AD

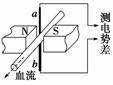
图8－4－17

2．如图8－4－15所示，光滑绝缘杆固定在水平位置上，使其两端分别带上等量同种正电荷Q₁、Q₂，杆上套着一带正电小球，整个装置处在一个匀强磁场中，磁感应强度方向垂直纸面向里，将靠近右端的小球从静止开始释放，在小球从右到左的运动过程中，下列说法中正确的是(　)

　 A．小球受到的洛伦兹力大小变化，但方向不变

　 B．小球受到的洛伦兹力将不断增大

　 C．小球的加速度先减小后增大

　 D．小球的电势能一直减小

　 解析：Q₁、Q₂连线上中点处电场强度为零，从中点向两侧电场强度增大且方向都指向中点，故小球所受电场力指向中点．小球从右向左运动过程中，小球的加速度先减小后增大，C正确．速度先增大后减小，洛伦兹力大小变化，由左手定则知，洛伦兹力方向不变，故A正确，B错误．小球的电势能先减小后增大，D错误．

　 答案：AC

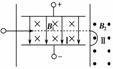
图8－4－16

1．如图8－4－14所示，实线表示在竖直平面内匀强电场的电场线，电场线与水平方向成α角，水平方向的匀强磁场与电场正交，有一带电液滴沿斜向上的虚线l做直线运动，l与水平方向成β角，且α>β，则下列说法中错误的是(　)

　 A．液滴一定做匀变速直线运动　　 B．液滴一定带正电

　 C．电场线方向一定斜向上　　　　 D．液滴一定做匀速直线运动

　 解析：在电磁场复合区域粒子一般不会做匀变速直线运动，因速度变化洛伦兹力变化，合外力一般变化．

答案：A

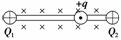
图8－4－15

5.

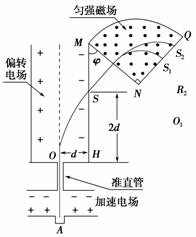
图8－4－13

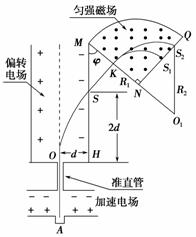
　 (2009·重庆，25)如图8－4－13所示，离子源A产生的初速度为零、带电荷量均为e、质量不同的正离子被电压为U₀的加速电场加速后匀速通过准直管，垂直射入匀强偏转电场，偏转后通过极板HM上的小孔S离开电场，经过一段匀速直线运动，垂直于边界MN进入磁感应强度为B的匀强磁场．已知HO＝d，HS＝2d，∠MNQ＝90°.(忽略离子所受重力)

　 (1)求偏转电场场强E₀的大小以及HM与MN的夹角φ；

　 (2)求质量为4m的离子在磁场中做圆周运动的半径；

　 (3)若质量为4m的离子垂直打在NQ的中点S₁处，质量为16m的离子打在S₂处，S₁和S₂之间的距离以及能打在NQ上的正离子的质量范围．

　 解析：(1)由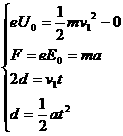

　 得E₀＝U₀/d，由tan φ＝，得φ＝45°.

　 (2)由

　 得R＝2 .

　 (3)将4m和16m代入R，得R₁、R₂，

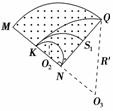
　 由ΔS＝－R₁，

　 将R₁、R₂代入得ΔS＝4(－1)

　 由R′²＝(2R₁)²+(R′－R₁)²，得R′＝R₁

　 由R₁<R<R₁，得m<m_x<25m.

　 答案：(1)45°　(2)2 　(3)4(－1) 　m<m_x<25m

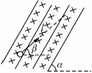
图8－4－14

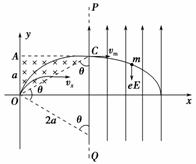
4．如图8－4－12所示，平行于直角坐标系y轴的PQ是用特殊材料制成的，只能让垂直打到PQ界面上的电子通过．其左侧有一直角三角形区域，分布着方向垂直纸面向里、磁感应强度为B的匀强磁场，其右侧有竖直向上场强为E的匀强电场．现有速率不同的电子在纸面上从坐标原点O沿不同方向射到三角形区域，不考虑电子间的相互作用．已知电子的电量为e，质量为m，在△OAC中，OA＝a，θ＝60°.求：

　 (1)能通过PQ界面的电子所具有的最大速度是多少；

　 (2)在PQ右侧x轴上什么范围内能接收到电子．

　 解析：(1)要使电子能通过PQ界面，电子飞出磁场的速度方向必须水平向右，由Bev＝m可知，r越大v越大，从C点水平飞出的电子，运动半径最大，对应的速度最大，即r＝2a时，电子的速度最大

　 由Bev_m＝m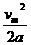，得：v_m＝.①

　 (2)粒子在电场中做类平抛运动，据

　 a＝t²②

　 x＝vt

　 得：x_max＝2Ba ③

　 由此可知：PQ界面的右侧x轴上能接收电子的范围是

　 本题属于复合场问题，考查带电粒子在有界磁场中的运动和带电粒子在匀强电场中的运动，需要同学们解题时能够正确地画出带电粒子在磁场和电场中的运动轨迹．

　 答案：(1)　(2)

3．如图8－4－11所示，竖直平面xOy内存在水平向右的匀强电场，场强大小E＝10 N/C，在y≥0的区域内还存在垂直于坐标平面向里的匀强磁场，磁感应强度大小B＝0.5 T．一带电量q＝+0.2 C、质量m＝0.4 kg的小球由长l＝0.4 m的细线悬挂于P点，小球可视为质点，现将小球拉至水平位置A无初速释放，小球运动到悬点P正下方的坐标原点O时，悬线突然断裂，此后小球又恰好能通过O点正下方的N点．(g＝10 m/s²)求：

　 (1)小球运动到O点时的速度大小；

　 (2)悬线断裂前瞬间拉力的大小；

　 (3)ON间的距离．

　 解析：(1)小球从A运动O的过程中，根据动能定理：mv²＝mgl－qEl①

　 则得小球在O点速度为：v＝ ＝2 m/s.②

　 (2)小球运动到O点绳子断裂前瞬间，对小球应用牛顿第二定律：

　 F_向＝F_T－mg－F_洛＝m③

　 F_洛＝Bvq④

　 由③、④得：F_T＝mg+Bvq+＝8.2 N．⑤

　 (3)绳断后，小球水平方向加速度a_x＝＝＝5 m/s²⑥

　 小球从O点运动至N点所用时间t＝＝0.8 s⑦

　 ON间距离h＝gt²＝3.2 m．⑧

　 答案：(1)2 m/s　(2)8.2 N　(3)3.2 m

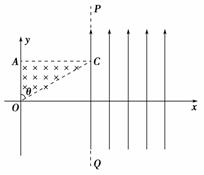
图8－4－12

2．如图8－4－10所示，界面PQ与水平地面之间有一个正交的匀强磁场B和匀强电场E，在PQ上方有一个带正电的小球A自O静止开始下落，穿过电场和磁场到达地面．设空气阻力不计，下列说法中正确的是(　)

　 A．在复合场中，小球做匀变速曲线运动

　 B．在复合场中，小球下落过程中的电势能减小

　 C．小球从静止开始下落到水平地面时的动能等于其电势能和重力势能的减少量总和

　 D．若其他条件不变，仅增大磁感应强度，小球从原来位置下落到水平地面时的动能不变

　 解析：小球受到磁场力，不可能做匀变速曲线运动．电场力做正功，电势能减小，由能量守恒知，C项正确．增大磁感应强度，会改变洛伦兹力，进而改变落地点，电场力做功会不同，D项错．

　 答案：BC

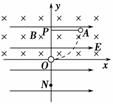
图8－4－11

1．如图8－4－9所示，空间存在一匀强磁场B(方向垂直纸面向里)和一电荷量为+Q的点电荷的电场，一带电粒子－q(不计重力)以初速度v₀从某处垂直于电场、磁场入射，初位置到点电荷+Q的距离为r，则粒子在电、磁场中的运动轨迹可能是(　)

　 A．沿初速度v₀方向的直线

　 B．以点电荷+Q为圆心，以r为半径，在纸面内的圆

　 C．初阶段在纸面内向右偏的曲线

　 D．初阶段在纸面内向左偏的曲线

　 解析：当带电粒子所受库仑力和洛伦兹力的合力正好能提供其所需的向心力时，粒子便以点电荷+Q为圆心，以r为半径，在纸面内做匀速圆周运动；因为点电荷+Q周围的电场是非匀强电场，所以粒子不可能做直线运动．综上所述粒子的运动轨迹可能为B、C、D.

　 答案：BCD

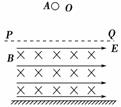
图8－4－10

12．如图9－1－29甲所示，一正方形金属线框位于有界匀强磁场区域内，线框的右边紧贴着边界．t＝0时刻对线框施加一水平向右的外力F，让线框从静止开始做匀加速直线运动，经过时间t₀穿出磁场，图9－1－29乙为外力F随时间t变化的图象．若线框质量m，电阻R及图象中F₀、t₀均为已知量，则根据上述条件，请你推出：

(1)磁感应强度B的计算表达式；

(2)线框左边刚离开磁场前瞬间的感应电动势E的计算表达式．

解析：(1)线框运动的加速度：a＝①

线框边长：l＝at②

线框离开磁场前瞬间有：v＝at₀③

由牛顿第二定律可知：3F₀－＝ma④

由①②③④式得，B＝ .⑤

(2)线框离开磁场前瞬间

感应电动势：E＝Blv⑥

联立②③⑤⑥式得：E＝ .

答案：(1) 　(2)

11．2008年9月25日，我国“神舟七号”载人飞船发射成功，在离地面大约200 km的太空运行．假设载人舱中有一边长为50 cm的正方形导线框，在宇航员操作下由水平方向转至竖直方向，此时地磁场磁感应强度B＝4×10^－5 T，方向如图9－1－28所示．

(1)该过程中磁通量的改变量是多少？

(2)该过程线框中有无感应电流？设线框电阻为R＝0.1 Ω，若有电流则通过线框的电量是多少？(sin 37°＝0.6，cos 37°＝0.8)

解析：(1)设线框在水平位置时法线n方向竖直向上，穿过线框的磁通量

Φ₁＝BScos 53°＝6.0×10^－6 Wb.

当线框转至竖直位置时，线框平面的法线方向水平向右，与磁感线夹角θ＝143°，穿过线框的磁通量Φ₂＝BScos 143°＝－8.0×10^－6 Wb

该过程磁通量的改变量大小ΔΦ＝Φ₁－Φ₂＝1.4×10^－5 Wb.

(2)因为该过程穿过闭合线框的磁通量发生了变化，所以一定有感应电流．根据电磁感应定律得，

＝＝.通过的电量为q＝·Δt＝＝1.4×10^{－4 C.}

答案：(1)1.4×10^－5 Wb　(2)1.4×10^{－4 C}

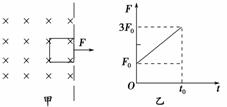
图9－1－29