3.一人站在平台上平抛一小球.球离手时的速度为v1，落地时的速度为v2.不计空气阻力，下图中能表示出速度矢量的演变过程的是(　)

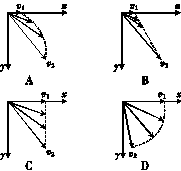
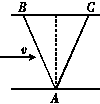解析：小球做平抛运动，水平方向的速度v1保持不变，竖直方向的速度不断变大，所以v2与水平方向的夹角变大.

答案：C

2.一个物体从某一确定的高度以v0的初速度水平抛出，已知它落地时的速度为vt，那么它的运动时间是(　)

A.　B.　C.　D.

解析：t＝＝.

答案：D

1.关于受力物体的运动情况，下列说法正确的是(　)

A.物体在恒力作用下不可能做曲线运动

B.物体在变力作用下有可能做曲线运动

C.做曲线运动的物体，其速度方向与合外力的方向不在同一直线上

D.物体在变力作用下不可能做直线运动

答案：BC

6.在一次摩托车跨越壕沟的表演中，摩托车从壕沟的一侧以v＝40 m/s的速度沿水平方向飞向另一侧，壕沟两侧的高度及宽度如图所示.摩托车前后轮的轴距为1.6 m，不计空气阻力.则摩托车是否能越过壕沟？请计算说明.

解析：题中摩托车安全跨越的平抛运动是指从后轮离地到后轮着地的过程.

设摩托车刚好能越过壕沟的初速度为v0，则：

水平方向有x＝v0t

竖直方向有h＝gt2

按题目要求可知：x＝20 m+1.6 m

h＝3.5 m－2.0 m＝1.5 m

代入上式有v0＝＝39.4 m/s

由于v＞v0，故摩托车能越过壕沟.

答案：能　计算过程略

金典练习八　运动的合成和分解　平抛运动

选择题部分共10小题，每小题6分.在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确.

5.如图所示，一网球运动员将球在边界处正上方垂直球网方向水平击出，球刚好过网落在图中位置，相关数据如图所示.下列说法正确的是(不计空气阻力)(　)

A.击球点的高度h1与球网的高度h2之间的关系为h1＝1.8h2

B.若保持击球高度不变，球的初速度v0只要大于，一定落在对方界内

C.任意降低击球高度(仍高于h2)，只要击球的初速度合适，球一定能落在对方界内

D.任意增加击球高度，只要击球初速度合适，球一定能落在对方界内

解析：h1＝g·()2

h1－h2＝g()2

解得：h1＝1.8h2，A正确.

当球被击出的初速度大于s时，球已飞出底界，故B错误.

当击球高度低于某一值时，无论初速度为多少，球要么不能过网，要么击出底界，C错误.

设击球高度为h0，以初速度vc击出的球恰好擦网而过压在底界上时，则有：

vc·＝s

vc·＝2s

解得h0＝h2，即击球高度大于h2时，只要初速度合适，球一定能落在对方界内，D正确.

答案：AD

4.如图甲所示，以9.8 m/s的水平初速度v0抛出的物体飞行一段时间后，垂直地撞在倾角θ为30°的斜面上，则物体完成这段飞行的时间为(　)

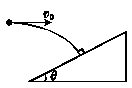A. s　B. s　C. s　D.2 s

解析：

乙

物体垂直地撞在斜面上，将其末速度分解如图乙所示.

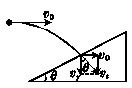cot θ＝＝

得：t＝＝ s

＝ s.

答案：C

3.如图所示，某人通过定滑轮用不可伸长的轻质细绳将质量为m的货物提升到高处.已知人拉绳的端点沿平面匀速向右运动，若滑轮的质量和摩擦均不计，则下列说法中正确的是(　)

A.货物匀速上升

B.货物加速上升

C.绳的拉力T大于物体的重力mg

D.绳的拉力T等于物体的重力mg

解析：假设某时刻绳与水平方向的夹角为θ，将手握着的绳端的速度沿绳方向和垂直绳方向分解，沿绳方向的分量等于货物上升的速度大小，即v′＝v·cos θ.由题图可知，绳与水平方向的夹角随时间减小，故货物做加速运动，T＞mg.

答案：BC

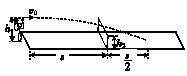
2.在抗洪抢险中，战士驾驶摩托艇救人，假设江岸是平直的，洪水沿江向下游流去，水流速度为v1，摩托艇在静水中的航速为v2，战士救人的地点A离岸边最近处O的距离为d.如果战士想在最短时间内将人送上岸，则摩托艇登陆的地点离O点的距离为(　)

A.d　B.0　C.d　D.d

解析：当摩托艇的船头垂直河岸方向航行时可在最短时间到岸.到岸时沿河岸方向的位移为x＝d.

答案：C

1.关于互成角度的两个初速度不为零的匀变速直线运动的合运动，下列说法正确的是(　)

A.一定是直线运动

B.一定是抛物线运动

C.可能是直线运动，也可能是加速度恒定的曲线运动

D.以上说法都不对

解析：当两运动的合加速度方向与合初速度的方向在同一直线上时物体做直线运动；当两运动的合加速与合初速度不在同一直线上时物体做加速度恒定的曲线运动.

答案：C

13.(14分)图示是汽车刹车时刹车痕(即刹车距离)与刹车前车速的关系图象.v为车速，s为车痕长度.

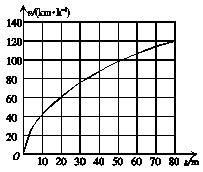
(1)尝试用动能定理解释汽车刹车距离与车速的关系.

(2)假设某汽车发生了车祸，已知该汽车刹车时的刹车距离与刹车前车速间的关系满足图示关系.交通警察要根据碰撞后两车的损害程度(与车子结构相关)、撞后车子的位移及转动情形等来估算碰撞时的车速，同时还要根据刹车痕判断撞前司机是否刹车及刹车前的车速.若估算出碰撞时车子的速度为45 km/h，碰撞前的刹车痕为20 m，则车子原来的车速是多少？

解析：(1)由图可得：v1＝60 km/h，s1＝20 m；v2＝120 km/h，s2＝80 m.由动能定理知：

－μmgs＝0－mv2

即v2＝2μgs

由图象数据知：＝，因此v－s图象是满足动能定理的一条抛物线.

(2)利用动能定理，有v2－v＝－2μgs0

在图象上取一点：v1＝60 km/h时，刹车位移s1＝20 m

即2μgs1＝v

所以v－452＝602

解得：v0＝75 km/h.

答案：(1)v－s图象是满足动能定理的一条抛物线

(2)75 km/h