3.如图所示，某同学将空的薄金属筒开口向下压入水中.设水温均匀且恒定，筒内空气无泄漏.不计气体分子间的相互作用，则被淹没的金属筒在缓慢下降过程中，筒内空气体积减小[2006年高考·重庆理综卷](　)

A.从外界吸热　　B.内能增大

C.向外界放热　 D.内能减小

解析：金属筒在下降过程中，水对筒的压强增大，因此气体的压强增大，气体体积减小，外界对气体做功.因水温恒定，气体内能不变，而外界对气体做了功，则气体应向外界放热，选项C正确.

答案：C

2.氧气钢瓶充气后压强高于外界大气压，假设缓慢漏气时瓶内外温度始终相等且保持不变，忽略氧气分子之间的相互作用.在该漏气过程中瓶内氧气[2007年高考·重庆理综卷](　)

A.分子总数减少，分子总动能不变

B.密度降低，分子平均动能不变

C.吸收热量，膨胀做功

D.压强降低，不对外做功

解析：①漏气过程分子总数减少，分子平均动能不变，总动能减少，选项A错误、B正确.

②气体漏气过程不断对外做功，要保持温度不变，瓶内气体通过钢瓶壁向外吸热，选项C正确、D错误.

　答案：BC

1.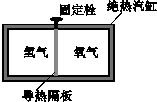如图所示，绝热汽缸中间用固定栓将可无摩擦移动的导热隔板固定，隔板质量不计，左右两室分别充有一定量的氢气和氧气(视为理想气体).初始时，两室气体的温度相等，氢气的压强大于氧气的压强，松开固定栓直至系统重新达到平衡，下列说法正确的是[2007年高考·江苏物理卷](　)

A.初始时氢分子的平均动能大于氧分子的平均动能

B.系统重新达到平衡时，氢气的内能比初始时的小

C.松开固定栓直至系统重新达到平衡的过程中，有热量从氧气传递到氢气

D.松开固定栓直至系统重新达到平衡的过程中，氧气的内能先增大后减小

解析：①初状态下由两气体的温度相等可知它们的平均动能相等，选项A错误.

②由隔板的导热性可知重新达到平衡时氢气、氧气的温度相等，且等于初状态下的温度，故氢、氧气体的内能都等于初状态下的内能，选项B错误.

③松开固定栓后隔板向右移动的过程，氧气内能增加，氢气内能减少，故有热量从氧气传向氢气才能使温度重新达到平衡，选项C、D正确.

答案：CD

5.在做“用油膜法估测分子的大小”的实验中，准备有以下器材：用酒精稀释过的油酸、滴管、痱子粉、浅盘及水、玻璃板、彩笔.还缺少的器材有　　　.若将1 cm³的油酸溶于酒精，制成200 cm³的油酸酒精溶液.已知1 cm³溶液有50滴，现取1滴油酸酒精溶液滴在水面上.随着酒精溶于水，油酸在水面上形成一单分子薄层.已测出这一薄层的面积为0.2 m²，由此可以估算出油酸分子的直径为　　　 m.

答案：量筒、坐标纸　5×10^－10

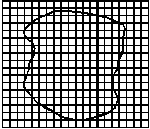
在做“用油膜法估测分子的大小”的实验中，所用酒精油酸溶液的浓度为每10⁴ mL溶液中有纯油酸6 mL，用注射器测得1 mL上述溶液为75滴.把1滴该溶液滴入盛水的浅盘里，待水面稳定后，将玻璃板放在浅盘上，用笔在玻璃板上描出油酸的轮廓形状，再把玻璃板放在坐标纸上，其形状如图所示，坐标中正方形方格的边长为1 cm.试求：

(1)油酸膜的面积是　　　　cm².

(2)每滴酒精油酸溶液中含有纯油酸的体积是　　mL.

(3)按以上实验数据估测出油酸分子直径为　　m.

答案：(1)157　(2)8×10^－6　(3)5×10^－10

第43讲　单 元 小 结

4.1967年，拖雷-坎永号油轮在英吉利海峡触礁，使大约8万吨原油溢出，污染了英国一百多公里的海岸线，使25000只海鸟死亡.石油流入海中危害极大，在海洋中泄漏1 t可覆盖12 km²的海面.由此可计算油膜的厚度约是分子直径数量级的　　倍.(设油的密度为0.91×10³ kg/m³，计算结果保留一位有效数字)

答案：9×10²

3.某学生在做“用油膜法估测分子的大小”的实验中，计算结果偏大，可能是由于(　)

A.油酸未完全散开

B.油酸中含有大量酒精

C.计算油膜面积时，舍去了所有不足一格的方格

D.求每滴体积时，1 mL的溶液的滴数多记了10滴

答案：AC

2.在“用油膜法估测分子的大小”的实验中，体积为V的油滴在水面上形成近似圆形的单分子油膜，油膜直径为D，则测得油分子的直径大约为(　)

A.　B.　C.　D.

答案：A

1.在做“用油膜法估测分子的大小”的实验中，实验简要步骤如下：

A.将画有油膜轮廓的玻璃板放在坐标纸上，数出轮廓内的方格数(不足半个的舍去，多于半个的算一个)，再根据方格的边长求出油膜的面积S

B.将一滴酒精油酸溶液滴在水面上，待油膜的形状稳定后，将玻璃板放在浅盘上，用彩笔将薄膜形状描画在玻璃板上

C.用浅盘装入约2 cm深的水，然后把痱子粉或石膏粉均匀地撒在水面上

D.用公式d＝，求出薄膜厚度，即为油酸分子的大小

E.根据酒精油酸溶液的浓度，算出一滴溶液中纯油酸的体积V

F.用注射器或滴管将事先配好的酒精油酸溶液一滴一滴地滴入量筒，记下量筒内增加一定体积时的滴数

上述实验步骤的合理顺序是：　　　　.

答案：CFBAED

13.(14分)游乐场的过山车可以底朝上在圆轨道上运行，游客却不会掉下来(如图甲所示).我们把这种情况抽象为图乙所示的模型：弧形轨道下端与竖直圆轨道相接，使小球从弧形轨道上端无初速度滚下，小球进入圆轨道下端后沿圆轨道运动，其中M、N分别为圆轨道的最低点和最高点.实验发现，只要h大于一定值，小球就可以顺利通过圆轨道的最高点.已知圆轨道的半径R＝5.0 m，小球的质量m＝1.0 kg，不考虑摩擦等阻力，取g＝10 m/s2.

(1)为使小球沿圆轨道运动而不掉下来，h至少为多大？

(2)如果h＝15 m，小球通过M点时轨道对小球的支持力FM为多大？

(3)高度h越大，小球滑至N点时轨道对小球的压力FN也越大，试推出FN关于h的函数关系式.

解析：(1)小球恰能通过N点时有：mg＝m

由机械能守恒定律：mg(h－2R)＝mv

解得：h＝R＝12.5 m.

(2)由机械能守恒定律：mgh＝mv

牛顿第二定律：FM－mg＝m

当h＝15 m时，解得：FM＝70 N.

(3)小球从h高处释放后至N点的过程有：

mg(h－2R)＝mv

在N处有：FN+mg＝m

解得：FN＝h－5mg＝4h－50 (h≥12.5 m).

答案：(1)12.5 m　(2)70 N

(3)FN＝4h－50 (h≥12.5 m)

12.(13分)图甲为电动打夯机的示意图，在电动机的转动轴O上装一个偏心轮，偏心轮的质量为m，其重心离轴心的距离为r.除偏心轮之外，整个装置其余部分的质量为M.当电动机匀速转动时，打夯机的底座在地面上跳动而将地面打实夯紧，试分析并回答：

(1)为了使底座刚好跳离地面，偏心轮的最小角速度ω0应是多少？

(2)如果偏心轮始终以这个角速度ω0转动，底座对地面压力的最大值为多少？

解析：由题意知，底座刚好跳离地面(或对地压力最大)时，偏心轮(m)的重心刚好在半径为r的圆周上的最高点(或最低点)，分别如图乙、丙所示：

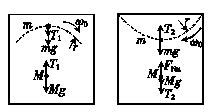
乙　　　　丙

(1)M刚好跳离地面时的受力分析如图乙所示：

所以对m有T1+mg＝mωr

对M有：T1－Mg＝0

解得：ω0＝.

(2)M对地的最大压力为FNm时的受力分析如图丙所示：

对m有：T2－mg＝mωr

对M有：FNm－Mg－T2＝0

解得：FNm＝2Mg+2mg.

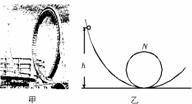答案：(1)ω0＝　(2)FNm＝2Mg+2mg