
题目列表(包括答案和解析)
8.(14分)如图所示,一质量为M的平板车B放在光滑水平面上,在其右端放一质量为m的小木块A,已知m<M,A、B间动摩擦因数为μ,现给A和B以大小相等、方向相反的初速度v0,使A开始向左运动,B开始向右运动,最后A不会滑离B,求:
(1)A、B最后的速度大小和方向.
(2)从地面上看,小木块向左运动到离出发点最远处时,平板车向右运动的位移大小.
解析:(1)A不会滑离B板,说明A、B具有相同的速度,设此速度为v, A和B的初速度的大小为v0,则据动量守恒定律可得:
Mv0-mv0=(M+m)v
解得:v=v0,方向向右.
(2)从地面上看,小木块向左运动到离出发点最远处时,木块速度为零,平板车速度为v′,由动量守恒定律得:
Mv0-mv0=Mv′
设这一过程平板向右运动距离s,则有:
μmgs=Mv-Mv′2
解得s=v.
答案:(1)v0,方向向右 (2)v
7.(13分)碰撞的恢复系数的定义为e=,其中v10和v20分别是碰撞前两物体的速度,v1和v2分别是碰撞后两物体的速度.弹性碰撞的恢复系数e=1,非弹性碰撞的恢复系数e<1.某同学借用“验证动量守恒定律”的实验装置(如图所示)验证弹性碰撞的恢复系数是否为1,实验中使用半径相等的钢质小球1和2(它们之间的碰撞可近似视为弹性碰撞),且小球1的质量大于小球2的质量.
 实验步骤如下:
实验步骤如下:
安装好实验装置,做好测量前的准备,并记下重垂线所指的位置O.
第一步,不放小球2,让小球1从斜槽上的A点由静止滚下,并落在地面上.重复多次,用尽可能小的圆把小球的所有落点圈在里面,其圆心就是小球落点的平均位置.
第二步,把小球2放在斜槽前端边缘处的C点,让小球1从A点由静止滚下,使它们碰撞.重复多次,并使用与第一步同样的方法分别标出碰撞后两小球落点的平均位置.
第三步,用刻度尺分别测量三个落地点的平均位置离O点的距离,即线段OM、OP、ON的长度.
在上述实验中,
(1)P点是 的平均位置,M点是 的平均位置,N点是 的平均位置.
(2)请写出本实验的原理:
.写出用测量值表示恢复系数的表达式: .
(3)三个落地点距O点的距离OM、OP、ON与实验所用的小球质量是否有关? .
答案:(1)在实验的第一步中小球1落点 小球1与小球2碰撞后小球1落点 小球2落点
(2)小球从槽口C飞出后做平抛运动的时间相同,设为t,则有OP=v10t,OM=v1t,ON=v2t
e=== (小球2碰撞前静止,v20=0)
(3)OP与小球的质量无关,OM和ON与小球的质量有关

6.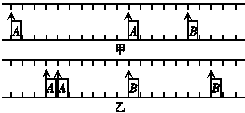 (12分)用气垫导轨验证动量守恒定律,滑块A、B可在导轨上无摩擦地滑动,导轨保持水平,导轨上附有每小格0.5
cm
的标尺.滑块质量分别为mA=0.14 kg,mB=0.22 kg,用每次间隔0.1 s的频闪拍摄两滑块在导轨上碰撞前后的运动情况.如图所示,图甲是碰撞前拍摄的照片示意图,当时A正在向右运动,B静止;图乙是碰撞后拍摄的照片示意图(两图中刻度不对应),当时A正在向左运动,B正在向右运动.
(12分)用气垫导轨验证动量守恒定律,滑块A、B可在导轨上无摩擦地滑动,导轨保持水平,导轨上附有每小格0.5
cm
的标尺.滑块质量分别为mA=0.14 kg,mB=0.22 kg,用每次间隔0.1 s的频闪拍摄两滑块在导轨上碰撞前后的运动情况.如图所示,图甲是碰撞前拍摄的照片示意图,当时A正在向右运动,B静止;图乙是碰撞后拍摄的照片示意图(两图中刻度不对应),当时A正在向左运动,B正在向右运动.
(1)碰撞前后两滑块的速度各为多少?
(2)碰撞前后两滑块的总动量各为多少?
(3)写出实验结论.
解析:(1)碰前速度
vA= m/s=0.5 m/s,vB=0.
碰后速度可能为:
vA′=±=±0.05 m/s
vB′= m/s=0.35 m/s
若vA′=0.05 m/s,则总动量增加,不可能存在,即只能vA′=-0.05 m/s
(2)碰前动量pA=mAvA=0.07 kg·m/s
碰后动量pA′+pB′=0.14×(-0.05)+0.22×0.35=0.07 kg·m/s.
(3)碰撞前后A、B的总动量守恒.
答案:(1)vA=0.5 m/s vB=0
vA′=-0.05 m/s vB′=0.35 m/s
(2)0.07 kg·m/s 0.07 kg·m/s
(3)碰撞前后A、B的总动量守恒
5.(12分)把两个大小相同、质量不等的金属小球用细线连接,中间夹一根被压缩了的轻质弹簧,置于摩擦可以不计的水平桌面上,如图所示.现烧断细线,观察两球的运动情况,并进行必要的测量,验证物体间相互作用时动量守恒.除图示器材外,实验室还准备了秒表、天平、直尺、螺旋测微器、铅锤、电磁打点计时器、木板、白纸、复写纸、图钉、细线等.
(1)多余的器材是: .
(2)需直接测量的物理是: .(要求明确写出物理量的名称和对应的符号)
(3)用所测得的物理量验证动量守恒定律的关系式是: .
(4)在本实验中还可测出每次压缩弹簧时的形变量Δx,以研究弹性势能与形变的关系,若分析实验数据发现Δx2正比于x+x,则说明弹簧的弹性势能Ep与弹簧形变Δx的关系为: .
答案:(1)秒表、螺旋测微器、电磁打点计时器 (2)两小球的质量m1、m2,两个小球做平抛运动的水平位移x1、x2 (3)m1x1=m2x2 (4)Ep∝Δx2
4.(12分)某同学设计了一个用打点计时器“验证动量守恒定律”的实验:如图甲所示,在小车A的前端黏有橡皮泥,在小车A后面连着纸带,电磁打点计时器的电源频率为50 Hz,长木板下垫着小木片用以平衡摩擦力.

甲
(1)若得到打点纸带如图乙所示,并测得各计数点间距离标在图上,A为运动起始的第一点,则应选 段来计算A和B碰后的共同速度.(填“AB”、“BC”、“CD”或“DE”)
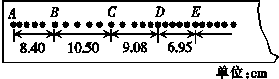
乙
(2)已测得小车A的质量为0.40 kg,小车B的质量为0.20 kg,由以上测量结果可得:碰前总动量为 kg·m/s,碰后总动量为 kg·m/s.
 答案:(1)DE (2)0.420 0.417
答案:(1)DE (2)0.420 0.417
3.(10分)图示为气垫导轨上两个滑块A、B相互作用后运动过程的频闪照片.频闪的频率为10 Hz.开始两个滑块静止,它们之间有一根被压缩的轻弹簧,滑块用绳子连接,绳子烧断后,两个滑块向相反方向运动.已知滑块A、B的质量分别为200 g、300 g.根据照片记录的信息,A、B离开弹簧后,A滑块做 运动,其速度大小为 ,本实验得出“在实验误差范围内,两木块组成的系统动量守恒”这一结论的依据是:
.
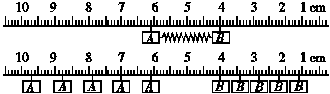
答案:匀速 0.09 m/s 释放弹簧前A、B的总动量为零;释放后pA=0.2×0.09 N·s=1.8×10-2 N·s,pB=-0.3× N·s=-1.8×10-2 N·s,pA+pB=0
2.某同学利用计算机模拟A、B两球碰撞来验证动量守恒,已知A、B两球质量之比为2∶3,用A球作入射球,初速度v1=1.2 m/s,让A球与静止的B球相碰,若规定以v1的方向为正,则该同学记录碰后的数据中,明显不合理的是( )
|
实验次数碰后小球速度(m·s-1) |
A |
B |
C |
D |
|
v1′ |
0.48 |
0.60 |
-1.20 |
0.24 |
|
v2′ |
0.48 |
0.40 |
1.60 |
0.96 |
解析:由动量守恒定律和能量的转化和守恒定律知,实验数据在误差允许范围内应满足:
m1v1=m1v1′+m2v2′
m1v≥m1v1′2+m2v2′2
又由两球的位置关系知:v1′≤v2′
可得B、C中数据不合理.
答案:BC
非选择题部分共7小题,共88分.
1.在做“验证动量守恒定律”的实验时,需要测定的物理量有( )
A.小球的质量 B.小球的半径
C.小球的飞行时间 D.小球的水平射程
答案:AD
3. 为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(即碰撞过程中没有机械能损失),某同学选取了两个体积相同、质量不相等的小球按下述步骤做了如下实验.
为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(即碰撞过程中没有机械能损失),某同学选取了两个体积相同、质量不相等的小球按下述步骤做了如下实验.
a.用天平测出两个小球1、2的质量(分别为m1和m2,且m1>m2).
b.按照图示安装好实验装置:将斜槽AB固定在桌边,使槽的末端点的切线水平,将一斜面BC连接在斜槽末端.
c.先不放小球2,让小球1从斜槽顶端的A处由静止开始滚下,记下小球在斜面上的落点位置.
d.将小球2放在斜槽前端边缘处,让小球1从斜槽顶端的A处滚下,使它们发生碰撞,记下小球1和小球2在斜面上的落点位置.
e.用毫米刻度尺量出各个落点位置到斜槽末端点B的距离.
图中D、E、F点是该同学记下的小球在斜面上的几个落点位置,到B点的距离分别为LD、LE、LF.
根据该同学的实验,回答下列问题:
(1)小球1与2发生碰撞后,1的落点是图中的 点,2的落点是图中的 点.
(2)用测得的物理量来表示,只要满足关系式 ,则说明碰撞中动量是守恒的.
(3)用测得的物理量来表示,只要再满足关系式 ,则说明两小球的碰撞是弹性碰撞.
解析:设斜面的倾角为θ,小球做平抛运动,由Lsin θ=gt2、Lcos θ=vt,得其抛出速度v ∝;验证动量是否守恒的表达式为m1v0=m1v1+m2v2,即m1=m1+m2;若没有机械能损失,则m1v=m1v+m2v,代入v ∝,得m1LE=m1LD+m2LF.
答案:(1)D F
(2)m1=m1+m2
(3)m1LE=m1LD+m2LF
金典练习十八 实验:验证动量守恒定律
选择题部分共2小题,每小题6分.在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确.
2. 如图所示,在实验室用两端带竖直挡板C、D的气垫导轨和有固定挡板的质量都是M的滑块A、B做“验证动量守恒定律”的实验,实验步骤如下:
如图所示,在实验室用两端带竖直挡板C、D的气垫导轨和有固定挡板的质量都是M的滑块A、B做“验证动量守恒定律”的实验,实验步骤如下:
a.把两滑块A、B紧贴在一起,在A上放质量为m的砝码,置于导轨上,用电动卡销卡住A、B,在A、B的固定挡板间放入一弹簧,使弹簧在水平方向上处于压缩状态.
b.按下电钮使电动卡销放开,同时启动记录两滑块运动时间的电子计时器,当滑块A、B与挡板C、D碰撞的同时,电子计时器自动停止计时,记下A至C的运动时间t1和B至D的运动时间t2.
c.将两滑块A、B仍置于原位置,重复几次上述实验,并对多次实验记录的t1、t2分别取平均值.
(1)在调整气垫导轨时,应注意 .
(2)应测量的数据还有 .
(3)只要满足关系式 ,即可验证动量守恒.
解析:由于滑块和气垫导轨间的摩擦力很小,可以忽略不计,可认为滑块在导轨上做匀速直线运动,因此两滑块作用后的速度可分别表示为:vA=,vB=.
若(M+m)=M成立,则(M+m)vA=MvB成立,即动量守恒.
答案:(1)用水平仪测量使导轨水平 (2)A至C板的距离L1,B至D板的距离L2 (3)(M+m)=M
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com