
题目列表(包括答案和解析)
5.福建省泉州市四校2010届高三上学期期末联考一列横波沿x轴传播,传播方向未知。t时刻与t+o.4s时刻波形相同,两时刻在x轴上-3m-3m的区间内的波形如图所示。由图像可以判定
①该波最大速度为10m/s
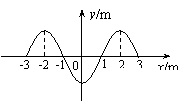 ②质点振动周期的最大值为0.4s
②质点振动周期的最大值为0.4s
③在t+o.2s时,x=3m的质点位移为零
④若波沿x轴正方向传播,各质点刚开始振动时的方向向上
上述说法中正确的是( B )
A.①② B.②③ C.③④ D.①④
4. 陕西省西安高新一中2010届高三高考模拟在波的传播方向上有A、B两质点,该两质点在振动过程中,相对平衡位置的位移始终相同,该两质点连线中点处的质点为C,则( B ) A 该两质点间的距离一定等于一个波长 B 该两质点的振动方向总是相同 C 质点C的振动方向一定和A的振动方向相反 D 当质点C处于波谷时,质点A.B一定处于波峰
3.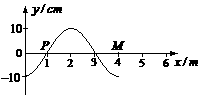 四川省内江市2010届高三二模模拟如图所示,一列简谐横波沿x轴正向传播,从波传到x=1m的P点时开始计时,已知在t=0.4s时PM间第一次形成图示波形,此时x=4m的M点正好在波谷。下列说法中正确的是 ( A )
四川省内江市2010届高三二模模拟如图所示,一列简谐横波沿x轴正向传播,从波传到x=1m的P点时开始计时,已知在t=0.4s时PM间第一次形成图示波形,此时x=4m的M点正好在波谷。下列说法中正确的是 ( A )
A.P点的振动周期为0.4s
B.P点开始振动的方向沿y 轴正方向
C.当M点开始振动时,P点正好在波谷
D.这列波的传播速度是7.5m/s
2.福建省泉州市四校2010届高三上学期期末联考一弹簧振子做简谐运动,周期为T,下列说法正确的是.( D )
A.若t时刻和(t+△t)时刻振子对平衡位置的位移大小相等,方向相同,则△t一定等于T的整数倍
B.若t时刻和(t+△t)时刻振子运动速度大小相等,方向相反,则△t一定等于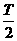 的整数倍
的整数倍
C.若△t=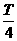 ,则t和(t+△t)两时刻,振子的位移大小之和一定等于振幅
,则t和(t+△t)两时刻,振子的位移大小之和一定等于振幅
D.若△t=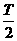 ,则在t时刻和(t+△t
,则在t时刻和(t+△t )时刻振子速度的大小一定相等
)时刻振子速度的大小一定相等
1.上海市七校2010届高三下学期联考关于机械波,下列说法不正确的是( A )
A.能在真空中传播 B.频率由波源决定
B.能产生干涉、衍射现象 D.在传播过程中能传递能量
5、用机械能守恒定律求变力做功
如果物体只受重力和弹力作用,或只有重力或弹力做功时,满足机械能守恒定律。如果求弹力这个变力做的功,可用机械能守恒定律来求解。
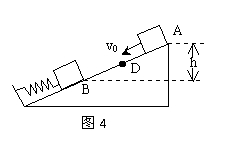 例5、如图4所示,质量m=2kg的物体,从光滑斜面的顶端A点以V0=5m/s的初速度滑下,在D点与弹簧接触并将弹簧压缩到B点时的速度为零,已知从A到B的竖直高度h=5m,求弹簧的弹力对物体所做的功。
例5、如图4所示,质量m=2kg的物体,从光滑斜面的顶端A点以V0=5m/s的初速度滑下,在D点与弹簧接触并将弹簧压缩到B点时的速度为零,已知从A到B的竖直高度h=5m,求弹簧的弹力对物体所做的功。
分析与解:由于斜面光滑故机械能守恒,但弹簧的弹力是变力,弹力对物体做负功,弹簧的弹性势能增加,且弹力做的功的数值与弹性势能的增加量相等。取B所在水平面为零参考面,弹簧原长处D 点为弹性势能的零参考点,则状态A:EA= mgh+mV02/2
对状态B:EB=-W弹簧+0
由机械能守恒定律得: W弹簧=-(mgh+mv02/2)=-125(J)。
 6、用功能原理求变力做功
6、用功能原理求变力做功
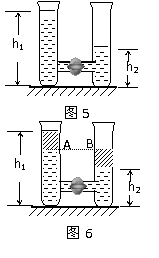
例6、两个底面积都是S的圆筒,放在同一水平面上,桶内装水,水面高度分别为h1和h2,如图5所示,已知水的密度为ρ。现把连接两桶的阀门打开,最后两桶水面高度相等,则这过程中重力所做的功等于 .
分析与解:由于水是不可压缩的,把连接两桶的阀门打开到两桶水面高度相等的过程中,利用等效法把左管高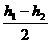 以上部分的水等效地移至右管,如图6中的斜线所示。最后用功能关系,重力所做的功等于重力势能的减少量,选用AB所在的平面为零重力势能平面,则画斜线部分从左管移之右管所减少的重力势能为:
以上部分的水等效地移至右管,如图6中的斜线所示。最后用功能关系,重力所做的功等于重力势能的减少量,选用AB所在的平面为零重力势能平面,则画斜线部分从左管移之右管所减少的重力势能为:
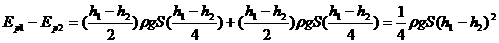
所以重力做的功WG=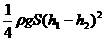 .
.
问题2:弄清滑轮系统拉力做功的计算方法
 当牵引动滑轮两根细绳不平行时,但都是恒力,此时若将此二力合成为一个恒力再计算这个恒力的功,则计算过程较复杂。但若等效为两个恒力功的代数和,将使计算过程变得非常简便。
当牵引动滑轮两根细绳不平行时,但都是恒力,此时若将此二力合成为一个恒力再计算这个恒力的功,则计算过程较复杂。但若等效为两个恒力功的代数和,将使计算过程变得非常简便。
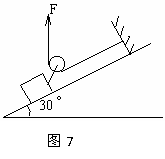
例7、如图7所示,在倾角为30°的斜面上,一条轻绳的一端固定在斜面上,绳子跨过连在滑块上的定滑轮,绳子另一端受到一个方向总是竖直向上,大小恒为F=100N的拉力,使物块沿斜面向上滑行1m(滑轮右边的绳子始终与斜面平行)的过程中,拉力F做的功是( )
A.100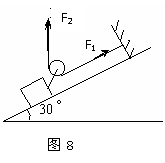 J B.150J
J B.150J
C.200J D.条件不足,无法确定
分析与解析:拉力F做的功等效为图8中F1、F2两个恒力所做功的代数和。即W=F1·S+F2Scos60°,而F1=F2=F=100N,所以
W=F·S(1+cos60°)=150J。即B选项正确。
问题3:弄清求某力的平均功率和瞬时功率的方法
例8、质量为m=0.5kg的物体从高处以水平的初速度V0=5m/s抛出,在运动t=2s内重力对物体做的功是多少?这2s内重力对物体做功的平均功率是多少?2s末,重力对物体做功的瞬时功率是多少?(g取 )
)
分析与解:t=2s内,物体在竖直方向下落的高度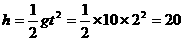 m,
m,
所以有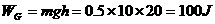 ,平均功率
,平均功率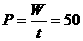 W。
W。
在t=2s末速度物体在竖直方向的分速度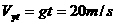 ,所以t=2s末瞬时功率
,所以t=2s末瞬时功率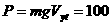 W。
W。
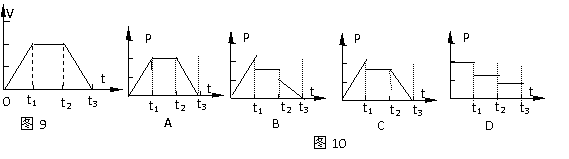 例9、起重机的钢索将重物由地面吊到空中某个高度,其速度图象如图9所示,则钢索拉力的功率随时间变化的图象可能是图10中的哪一个?
例9、起重机的钢索将重物由地面吊到空中某个高度,其速度图象如图9所示,则钢索拉力的功率随时间变化的图象可能是图10中的哪一个?
分析与解:在0-t1时间内,重物加速上升,设加速度为a1,则据牛顿第二定律可得钢索的拉力F1=mg+ma1,速度Vt=a1t,所以拉力的功率为:P1=m(a1+g)a1t;
在t1-t2时间内,重物匀速上升,拉力F2=mg,速度为V1=a1t1,所以拉力的功率为:
P2=mga1t1.
在t2-t3时间内,重物减速上升,设加速度大小为a2,则据牛顿第二定律可得钢索的拉力F2=mg-ma2,速度V2=a1t1-a2t,所以拉力的功率为:P1=m(g-a2)(a1t1-a2t).
综上所述,只有B选项正确。
问题4:机车起动的最大速度问题
例10、汽车发动机额定功率为60 kW,汽车质量为5.0×103 kg,汽车在水平路面行驶时,受到的阻力大小是车重的0.1倍,试求:汽车保持额定功率从静止出发后能达到的最大速度是多少?
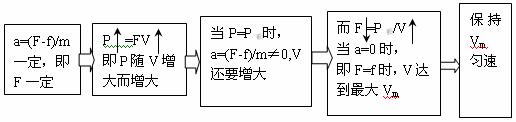
分析与解:汽车以恒定功率起动时,它的牵引力F将随速度V的变化而变化,其加速度a也随之变化,具体变化过程可采用如下示意图表示:
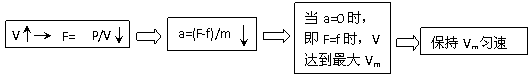
由此可得汽车速度达到最大时,a=0,
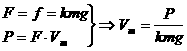 =12 m/s
=12 m/s
小结:机车的速度达到最大时,一定是机车的加速度为零。弄清了这一点,利用平衡条件就很容易求出机车的最大速度。
问题5:机车匀加速起动的最长时间问题
例11、 汽车发动机额定功率为60 kW,汽车质量为5.0×103 kg,汽车在水平路面行驶时,受到的阻力大小是车重的0.1倍,试求:若汽车从静止开始,以0.5 m/s2的加速度匀加速运动,则这一加速度能维持多长时间?
分析与解:要维持汽车加速度不变,就要维持其牵引力不变,汽车功率将随V增大而增大,当P达到额定功率P额后,不能再增加,即汽车就不可能再保持匀加速运动了.具体变化过程可用如下示意图表示:
所以,汽车达到最大速度之前已经历了两个过程:匀加速和变加速,匀加速过程能维持到汽车功率增加到P额的时刻,设匀加速能达到最大速度为V1,则此时

小结:机车匀加速度运动能维持多长时间,一定是机车功率达到额定功率的时间。弄清了这一点,利用牛顿第二定律和运动学公式就很容易求出机车匀加速度运动能维持的时间。
问题6:机车运动的最大加速度问题。
例12、电动机通过一绳子吊起质量为8 kg的物体,绳的拉力不能超过120 N,电动机的功率不能超过1200 W,要将此物体由静止起用最快的方式吊高90 m(已知此物体在被吊高接近90 m时,已开始以最大速度匀速上升)所需时间为多少?
分析与解:此题可以用机车起动类问题的思路,即将物体吊高分为两个过程处理:第一过程是以绳所能承受的最大拉力拉物体,使物体以最大加速度匀加速上升,第一个过程结束时,电动机刚达到最大功率.第二个过程是电动机一直以最大功率拉物体,拉力逐渐减小,当拉力等于重力时,物体开始匀速上升.
在匀加速运动过程中加速度为
a=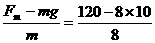 m/s2=5 m/s2,末速度Vt=
m/s2=5 m/s2,末速度Vt=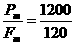 =10 m/s
=10 m/s
上升的时间t1=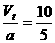 s=2 s,上升高度为h=
s=2 s,上升高度为h=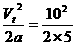 =10 m
=10 m
在功率恒定的过程中,最后匀速运动的速率为
Vm=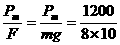 =15 m/s
=15 m/s
外力对物体做的总功W=Pmt2-mgh2,动能变化量为
ΔEk=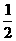 mV2m-
mV2m-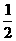 mVt2
mVt2
由动能定理得Pmt2-mgh2=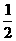 mVm2-
mVm2-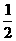 mVt2
mVt2
代入数据后解得t2=5.75 s,所以t=t1+t2=7.75 s所需时间至少为7.75 s.
小结:机车运动的最大加速度是由机车的最大牵引力决定的,而最大牵引力是由牵引物的强度决定的。弄清了这一点,利用牛顿第二定律就很容易求出机车运动的最大匀加速度。
4、用动能定理求变力做功
例4、如图3所示,AB为1/4圆弧轨道,半径为0.8m,BC是水平轨道,长L=3m,BC处的摩擦系数为1/15,今有质量m=1kg的物体,自A点从静止起下滑到C点刚好停止。求物体在轨道AB段所受的阻力对物体做的功。
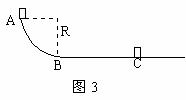
分析与解:物体在从A滑到C的过程中,有重力、AB段的阻力、AC段的摩擦力共三个力做功,重力做功WG=mgR,水平面上摩擦力做功Wf1=-μmgL,由于物体在AB段受的阻力是变力,做的功不能直接求。根据动能定理可知:W外=0,
所以mgR-umgL-WAB=0
即WAB=mgR-umgL=6(J)
3、平均力法
如果力的方向不变,力的大小对位移按线性规律变化时,可用力的算术平均值(恒力)代替变力,利用功的定义式求功。
例3、一辆汽车质量为105kg,从静止开始运动,其阻力为车重的0.05倍。其牵引力的大小与车前进的距离变化关系为F=103x+f0,f0是车所受的阻力。当车前进100m时,牵引力做的功是多少?
分析与解:由于车的牵引力和位移的关系为F=103x+f0,是线性关系,故前进100m过程中的牵引力做的功可看作是平均牵引力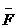 所做的功。由题意可知f0=0.05×105×10N=5×104N,所以前进100m过程中的平均牵引力:
所做的功。由题意可知f0=0.05×105×10N=5×104N,所以前进100m过程中的平均牵引力:
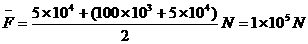
∴W=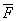 S=1×105×100J=1×107J。
S=1×105×100J=1×107J。
2、微元法
当物体在变力的作用下作曲线运动时,若力的方向与物体运动的切线方向之间的夹角不变,且力与位移的方向同步变化,可用微元法将曲线分成无限个小元段,每一小元段可认为恒力做功,总功即为各个小元段做功的代数和。
例2、如图2所示,某力F=10N作用于半径R=1m的转盘的边缘上,力F的大小保持不变,但方向始终保持与作用点的切线方向一致,则转动一周这个力F做的总功应为:
A、0J B、20πJ C、10J D、20J
分析与解:把圆周分成无限个小元段,每个小元段可认为与力在同一直线上,故ΔW=FΔS,则转一周中各个小元段做功的代数和为W=F×2πR=10×2πJ=20πJ=62.8J,故B正确。
1、等值法
等值法即若某一变力的功和某一恒力的功相等,则可以通过计算该恒力的功,求出该变力的功。而恒力做功又可以用W=FScosa计算,从而使问题变得简单。
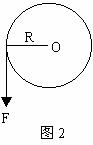
例1、如图1,定滑轮至滑块的高度为h,已知细绳的拉力为F(恒定),滑块沿水平面由A点前进S至B点,滑块在初、末位置时细绳与水平方向夹角分别为α和β。求滑块由A点运动到B点过程中,绳的拉力对滑块所做的功。
分析与解:设绳对物体的拉力为T,显然人对绳的拉力F等于T。T在对物体做功的过程中大小虽然不变,但其方向时刻在改变,因此该问题是变力做功的问题。但是在滑轮的质量以及滑轮与绳间的摩擦不计的情况下,人对绳做的功就等于绳的拉力对物体做的功。而拉力F的大小和方向都不变,所以F做的功可以用公式W=FScosa直接计算。由图1可知,在绳与水平面的夹角由α变到β的过程中,拉力F的作用点的位移大小为:
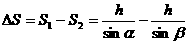
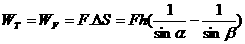
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com