4.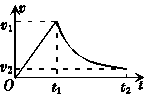在军事演习中，某空降兵从飞机上跳下，先做自由落体运动，在t1时刻，速度达较大值v1时打开降落伞做减速运动，在t2时刻以较小的速度v2着地.他的速度图象如图所示.下列关于该空降兵在0-t2或t1-t2时间内的平均速度的结论中，正确的是(　)

A.0-t2时间内＝

B.t1-t2时间内＝

C.t1-t2时间内>

D.t1-t2时间内<

解析：在0-t1时间内1＝

在t1-t2时间内2＜

故选项B、C错误、D正确.

对于0-t2时间内的平均速度，有＜、＝和＞三种可能，无法判定二者的关系，故选项A错误.

答案：D

3.两辆游戏赛车a、b在两条平行的直车道上行驶.t＝0时两车都在同一计时线处，此时比赛开始.它们的四次比赛中的v－t图象如图所示.下列图象对应的比赛中，有一辆赛车追上了另一辆的是[2007年高考·海南物理卷](　)

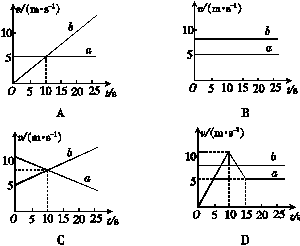
解析：在A、C图象中，在t＝20 s时刻b车追上a车.

答案：AC

2.下列给出的四组图象中，能够反映同一直线运动的是(　)

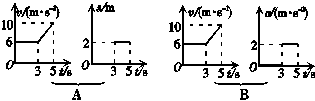
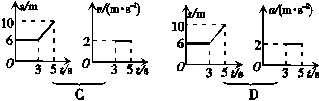
答案：BC

1.甲、乙两辆汽车在平直的公路上沿同一方向做直线运动，t＝0时刻同时经过公路旁的同一个路标.在描述两车运动的v－t图象中(如图所示)，直线a、b分别描述了甲、乙两车在0-20 s的运动情况.关于两车之间的位置关系，下列说法正确的是[2007年高考·宁夏理综卷](　)

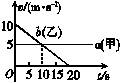
A.在0-10 s内两车逐渐靠近

B.在10-20 s内两车逐渐远离

C.在5-15 s内两车的位移相等

D.在t＝10 s时两车在公路上相遇

答案：C

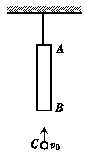
5.如图所示，长为0.5 m的圆筒AB悬挂于天花板上，在AB的正下方有直径小于圆筒内径的小钢球C，C距圆筒下端B的距离h＝2 m.某时刻烧断悬挂AB的悬绳，同时将小钢球C以v0＝20 m/s的初速度竖直上抛.空气阻力不计，取g＝10 m/s2，求小钢球C从圆筒AB中穿过的时间.

解析：解法一　取C上抛位置处为位移参考点，向上为正方向，则：

sA＝h+l－gt2

sB＝h－gt2

sC＝v0t－gt2

故C与B相遇的时刻有：sB＝sC

解得：t1＝＝0.1 s

　C与A相遇的时刻有：sA＝sC

解得：t2＝＝0.125 s

故C从AB中穿过的时间Δt＝t2－t1＝0.025 s.

解法二　考虑圆筒与钢球的速度，则：

vAB＝－gt，vC＝v0－gt

故它们的相对速度v相＝vC－vAB＝v0

所以C从AB中穿过的时间Δt＝＝0.025 s.

答案：0.025 s

第11讲　运动图象　追赶问题

体验成功

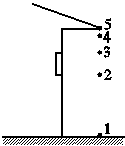
4.屋檐上每隔相同的时间间隔滴下一滴水，当第5滴正欲滴下时，第1滴恰好到达地面，而第3滴与第2滴分别位于高为1 m的窗户的上下缘，如图所示.取g＝10 m/s2，问：

(1)此屋檐离地面多高？

(2)滴水的时间间隔是多少？

解析：(1)可以将这5滴水的运动等效地视为一滴水的下落，并对这一滴水的运动全过程分成4个相等的时间间隔，图中相邻的两滴水间的距离分别对应着各个相等时间间隔内的位移，它们满足比例关系：1∶3∶5∶7.设相邻水滴之间的距离自上而下依次为：x、3x、5x、7x，则窗户高为5x，依题意有5x＝1 m，则x＝0.2 m.

屋檐高度h＝x+3x+5x+7x＝16x＝3.2 m.

(2)由h＝gt2

得：t＝＝ s＝0.8 s

所以滴水的时间间隔Δt＝＝0.2 s.

答案：(1)3.2 m　(2)0.2 s

3.在地质、地震、勘探、气象和地球物理等领域的研究中，需要精确的重力加速度g值，g值可由实验精确测定.近年来测g值的一种方法叫“对称自由下落法”，它是将测g值归于测长度和时间，以稳定的氦氖激光的波长为长度标准，用光学干涉的方法测距离，以铷原子钟或其他手段测时间，此方法能将g值测得很准.具体做法是：将真空长直管沿竖直方向放置，自其中的O点向上抛小球，从抛出小球至小球又落回抛出点的时间为T2；小球在运动过程中经过比O点高H的P点，小球离开P点至又回到P点所用的时间为T1.由T1、T2和H的值可求得g等于(　)

A.　 B.

C.　 D.

解析：设小球上升的最大高度为h，由题意知：

h＝g()2

h－H＝g()2

解得：g＝.

答案：A

2.两个小球分别拴在一根轻绳的两端，一人用手拿住一球将它们从三楼阳台上由静止释放，两球先后落地的时间差为Δt1；若将它们从四楼阳台上由静止释放，则它们落地的时间差为Δt2.不计空气阻力，则Δt1、Δt2满足(　)

A.Δt1＝Δt2　 B.Δt1＜Δt2

C.Δt1＞Δt2　 D.以上都有可能

解析：时间差等于轻绳长度除以下面小球落地后上面小球运动的平均速度，故Δt1＞Δt2.

答案：C

6.利用打点计时器研究一个约1.4 m高的商店卷帘窗的运动.将纸带粘在卷帘底部，纸带通过打点计时器随帘在竖直面内向上运动.打印后的纸带如图甲所示，数据如图乙中的表格所示.纸带中A与B、B与C、C与D……每两点之间的时间间隔为0.10 s，根据各间距的长度，可计算出卷帘窗在各间距内的平均速度v平均，可以将v平均近似地作为该间距中间时刻的即时速度v.

(1)请根据所提供的纸带和数据，在图丙中绘出卷帘窗的v－t图象.

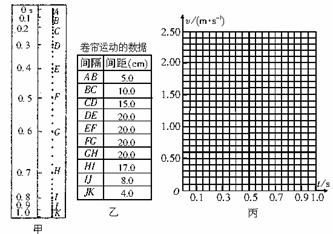
(2)AD段的加速度为　　m/s2，AK段的平均速度为　　m/s.

解析：(1)根据所提供的纸带和数据求各间距内的平均速度v平均＝(si表示两计时点间的距离，Δt表示每两计时点间的时间间隔).由题意可确定0.05 s、0.15 s、 0.25 s……各时刻的即时速度，将计算数据列入下面的表格中，绘出的v－t图象参见答案.

(2)由v－t图象可知AD段卷帘做匀加速运动，由速度公式：

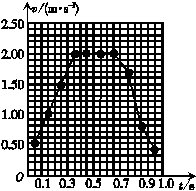DE－AB＝a·3Δt

或逐差法：a＝

均可求得：a＝5 m/s2

故AK段的平均速度为：

AK＝＝ m/s＝1.39 m/s.

答案：(1)如图丁所示　(2)5　1.39

5.一个有一定厚度的圆盘可以绕通过中心且垂直于盘面的水平轴转动.用下面的方法测量它匀速转动的角速度.

实验器材：电磁打点计时器、米尺、纸带、复写纸片.

实验步骤：

①如图甲所示，将电磁打点计时器固定在桌面上，将纸带的一端穿过打点计时器的限位孔后，固定在待测圆盘的侧面上，使得圆盘转动时，纸带可以卷在圆盘侧面上；

②启动控制装置使圆盘转动，同时接通电源，打点计时器开始打点；

③经过一段时间后，停止转动和打点，取下纸带，进行测量.

(1)用已知量和测得量表示角速度的表达式为ω＝　　　，式中各量的意义是　　　　　.

(2)某次实验测得圆盘半径r＝5.50×10－2 m，得到的一段时间内的纸带如图乙所示.若打点计时器所接交流电源的频率为50 Hz，则可得角速度为　　 rad/s.

乙

解析：纸带移动速度v＝，又v＝ωr，因此ω＝，其中x1、x2为所取段端点打点的坐标，T为电磁打点计时器打点的时间间隔，n为所取段的打点数(含端点)，r为圆盘半径.取图乙中所有打点，则：x2＝11.30 cm，x1＝0.75 cm，n＝15.将r、T一并代入公式可得：ω＝6.85 rad/s.

答案：(1)　其中x1、x2为所取段端点打点的坐标，T为电磁打点计时器打点的时间间隔，n为所取段的打点数(含端点)，r是圆盘半径　(2)6.85