6.A、B两球沿同一条直线运动，图示的s－t图象记录了它们碰撞前后的运动情况，其中a、b分别为A、B碰撞前的s－t图线，c为碰撞后它们的s－t 图线.若A球质量为1 kg，则B球质量是(　)

A.0.17 kg　B.0.34 kg　C.0.67 kg　D.1.00 kg

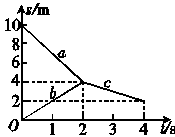解析：由图象可知碰撞前两者做匀速直线运动的速度分别为：

v_a＝ m/s＝－3 m/s，v_b＝ m/s＝2 m/s

碰撞后二者粘在一起做匀速直线运动的速度为：

v_c＝ m/s＝－1 m/s

由于碰撞过程中动量守恒，则有：

m_Av_a+m_Bv_b＝(m_A+m_B)v_c

可解得：m_B＝0.67 kg.

答案：C

5.如图甲所示，一轻弹簧的两端与质量分别为m₁和m₂的两物块A、B相连接，并静止在光滑的水平面上.现使B瞬时获得水平向右的速度v＝3 m/s，以此刻为计时起点，两物块的速度随时间变化的规律如图乙所示，从图象信息可得(　)

A.在t₁、t₃时刻两物块达到共同速度1 m/s，且弹簧都处于伸长状态

B.两物体的质量之比m₁∶m₂＝2∶1

C.在t₂时刻A与B的动能之比E_k1∶E_k2＝4∶1

D.从t₃到t₄时刻弹簧由压缩状态恢复到原长

解析：在t₁、t₃时刻两物体达到共同速度1 m/s，其中t₁时刻弹簧处于伸长状态，t₃时刻弹簧处于压缩状态.故选项A错误.

由动量守恒定律得：m₂×3＝(m₁+m₂)×1

解得：m₁∶m₂＝2∶1，故选项B正确.

在t₂时刻E_k1∶E_k2＝m₁×2²∶m₂×1²＝8∶1，故选项C错误.

在t₄时刻A、B相对速度最大，弹簧处于原长状态，故选项D正确.

答案：BD

4.如图所示，半圆槽M置于光滑的水平面上.现从半圆槽右端入口处静止释放一质量为m的小球，则小球释放后，以下说法中正确的是(　)

A.若圆弧面光滑，则系统动量守恒

B.若圆弧面光滑，则小球能滑至半圆槽左端入口处

C.若圆弧面不光滑，则小球不能滑至半圆槽左端入口处，且小球到达最左端时，系统有向右的速度

D.若圆弧面不光滑，则小球不能滑至半圆槽左端入口处，但小球到达最左端时，系统速度为零

解析：无论槽是否光滑，这一过程系统竖直方向的动量都不守恒，而水平方向上系统的动量守恒.

当弧面光滑时，系统机械能守恒.设小球释放后到达槽的最右端的高度为h，共同速度为v，有：

(m+M)×0＝(m+M)v

mgR＝mgh+(m+M)v²

解得：v＝0，h＝R.

答案：BD

3.如图所示，甲、乙两人各站在静止小车的左右两端，当他俩同时相向行走时，发现小车向右运动.下列说法不正确的是(车与地面之间无摩擦)(　)

A.乙的速度必定大于甲的速度

B.乙对小车的冲量必定大于甲对小车的冲量

C.乙的动量必定大于甲的动量

D.甲、乙动量总和必定不为零

解析：甲、乙及小车组成的系统水平方向动量守恒、总动量为零，当小车向右运动时，说明甲、乙两人的总动量水平向左，乙对小车向右的冲量大于甲对小车向左的冲量.

答案：A

2.一颗手榴弹以v₀＝10 m/s的水平速度在空中飞行.设它爆炸后炸裂为两块，小块质量为0.2 kg，沿原方向以250 m/s的速度飞去，那么，质量为0.4 kg的大块在爆炸后速度大小和方向是(　)

A.125 m/s，与v₀反向　　　B.110 m/s，与v₀反向

C.240 m/s，与v₀反向　 D.以上答案均不正确

解析：由动量守恒定律有：Mv₀＝m₁v₁+m₂v₂

即0.6×10＝0.2×250+0.4v₂

解得：v₂＝－110 m/s，负号表示方向与v₀相反.

答案：B

1.如图所示，小车放在光滑的水平面上，先将小球拉到一定的角度，然后同时放开小球和小车，那么在以后的过程中(　)

A.小球向左摆动时，小车也向左运动，且小球与小车组成的系统动量守恒

B.小球向左摆动时，小车向右运动，且小球与小车组成的系统动量守恒

C.小球向左摆到最高点时，小球的速度为零，而小车速度不为零

D.在任何时刻，小球和小车在水平方向上的动量一定大小相等、方向相反

答案：D

6.用火箭发射人造卫星时，假设最后一节火箭的燃料用完后，火箭壳体和卫星一起以v＝7.0×10³ m/s的速度绕地球做匀速圆周运动.已知卫星的质量m＝500 kg，最后一节火箭壳体的质量M＝100 kg.某时刻火箭壳体与卫星分离，分离时卫星与火箭壳体沿轨道切线方向的相对速度u＝1.8×10³ m/s，试计算分离后瞬间卫星的速度和火箭壳体的速度.(以地面为参考系)

解析：设分离后卫星与火箭壳体相对地面的速度分别为v₁和v₂，分离时系统在轨道切线方向上动量守恒，有：

(m+M)v＝mv₁+Mv₂

又u＝v₁－v₂

解得：v₁＝7.3×10³ m/s

v₂＝5.5×10³ m/s.

答案：7.3×10³ m/s　5.5×10³ m/s

金典练习十六　动量守恒定律及其应用

选择题部分共10小题，每小题6分.在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确.

5.如图所示，人在平板车上用水平恒力拉绳使重物能逐渐靠近自己，人相对车始终不动，重物与平板车之间、平板车与地面之间均无摩擦.设开始拉重物时车和重物都是静止的，车和人的总质量M＝100 kg ，重物的质量m＝50 kg，拉力F＝200 N，重物在车上向人靠近了3 m，求：

(1)车在地面上移动的距离.

(2)这时车和重物的速度.

解析：(1)设重物在车上向人靠近L＝3 m时，车在地面上移动的距离为s，依题意有：

m(L－s)＝Ms

整理得：s＝1 m.

(2)人和车的加速度a＝＝ m/s²＝2 m/s²

则人和车在地面上移动1 m时的速度为：

v＝＝2 m/s

此时物体的对地速度为v_物，根据mv_物＝Mv得：

v_物＝4 m/s.

答案：(1)1 m　(2)4 m/s

4.小球1追碰小球2，碰撞前两球的动量分别为p₁＝5 kg·m/s，p₂＝7 kg·m/s，正碰后小球2的动量p₂′＝10 kg·m/s.则两球的质量关系可能是(　)

A.m₂＝m₁　　　B.m₂＝2m₁

C.m₂＝4m₁　 D.m₂＝6m₁

解析：由动量守恒定律，很容易得到碰后小球1的动量p₁′＝2 kg·m/s，这丝毫不能反映出两球的质量关系，这就要从题中内含的其他关系去寻找.

首先，“追碰”表明碰前小球1的速度大于小球2的速度，即v₁＞v₂，由v＝可得，＞，即m₂＞，排除了选项A的可能.

按同样思路，碰后应有v₁′≤v₂′，≤，有m₂≤5m₁，排除了选项D的可能.

由动能不增原则可知：E_k1+E_k2≥E_k1′+E_k2′，由动能E_k与动量p的关系：E_k＝

可得：+≥+

即有：m₂≥，排除了选项B的可能.

综合以上结论得：≤m₂≤5m₁，只有选项C正确.

答案：C

3.A、B两球在光滑水平面上相向运动，已知m_A＞m_B，当两球相碰后，其中一球停止运动，则可断定(　)

A.碰前A的动量与B的动量大小相等

B.碰前A的动量大于B的动量

C.若碰后A的速度为零，则碰前A的动量大于B的动量

D.若碰后B的速度为零，则碰前A的动量大于B的动量

解析：碰后只有一球静止，说明系统总动量不为零，选项A错误；由于不知道哪个球停止，则不能判断碰前谁的动量大，B错误；由于二球相向运动，一球停止，另一球的运动方向必与其原运动方向反向，总动量与静止球原动量方向相同，因此选项C正确.

答案：C