7.如图甲所示，一粗细均匀的U形管内装有一定量水银竖直放置，右管口用盖板A密闭一部分气体，左管口开口，两液面高度差为h，U形管中水银柱总长为4h.现拿去盖板，水银柱开始流动，当两侧液面第一次相平时，右侧液面下降的速度大小为多少？(水银柱与管壁之间的阻力不计)

解析：

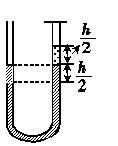如图乙所示，当右侧液面下降时，两侧液面达到同一水平，这一过程中水银柱的重力势能变化为：

ΔE_p＝－ρS··g·

其中ρ、S分别水银的密度和水银柱的横截面积

由机械能守恒定律得：

－ΔE_p＝ΔE_k，即ρs··g·＝ρS·4h·v²

可解得：v＝.

答案：

金典练习十二　势能　重力做功　机械能守恒定律

选择题部分共10小题，每小题6分.在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确.

6.如图所示，质量m＝2 kg的小球系在轻弹簧的一端，另一端固定在悬点O处，将弹簧拉至水平位置A处(弹簧处于原长)由静止释放，小球到达O点的正下方距O点h＝0.5 m处的B点时速度v＝2 m/s.求小球从A运动到B的过程中弹簧弹力做的功.(取g＝10 m/s²)

解析：小球在运动过程中只受重力和弹力的作用，故系统机械能守恒，以B点为重力势能零势面，A点为弹性势能零势面，则：

在初状态A有：E₁＝E_k1+E_p1＝mgh

在末状态B有：E₂＝E_k2+E_p2＝mv²+E_p2

式中E_p2为弹簧的弹性势能，由机械能守恒定律有：

E₁＝E₂

即mgh＝mv²+E_p2

解得：E_p2＝mgh－mv²

＝2×10×0.5 J－×2×2² J

＝6 J

因为弹性势能增加，弹簧的弹力做负功，故弹簧的弹力做的功为W_弹＝－ΔE_p＝－6 J.

答案：－6 J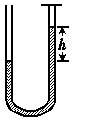

5.如图所示，一根轻杆长为2L，中点A和右端点B各固定一个小球，m_B＝2m_A左端O为光滑水平转轴.开始时杆静止在水平位置，释放后将向下摆动至竖直，在此过程中以下说法正确的是(　)

A.A、B两球的机械能都守恒

B.A、B两球的机械能不守恒，但它们组成的系统机械能守恒

C.这一过程O、A间轻杆对A球做正功

D.这一过程A、B间轻杆对A球做正功

解析：两小球及轻杆组成的系统的机械能守恒，设摆到竖直时角速度为ω，有：

m(Lω)²+·2m(2Lω)²＝mgL+2mg·2L

解得：ω＝

即A的动能E_kA＝m(ωL)²＝mgL＜|ΔE_pA|

B的动能E_kB＝·2m(ω·2L)²

＝·2mg·2L＞|ΔE_pB|

故选项A错误、B正确.

又因为下摆的过程O、A间轻杆的弹力沿杆方向不做功，故知A、B之间轻杆对A球做负功.

答案：B

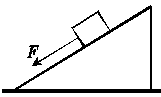
4.用平行于斜面向下的拉力F将一个物体沿斜面往下拉动后，拉力的大小等于摩擦力，则

A.物体做匀速运动

B.合外力对物体做功等于零

C.物体的机械能减少

D.物体的机械能不变

解析：物体所受的力中，重力、拉力、摩擦力对物体做功，拉力与摩擦力做的功相互抵消，重力做功不影响机械能，故物体的机械能不变.

答案：D

3.如图所示，长为L的轻杆一段固定一质量为m的小球，另一端安装有固定转动轴O，杆可在竖直平面内绕O无摩擦转动.若在最低点P处给小球一沿切线方向的初速度v₀＝2，不计空气阻力，则下列说法正确的是(　)

A.小球不可能到达圆周轨道的最高点Q

B.小球能达到圆周轨道的最高点Q，且在Q点受到轻杆向上的支持力

C.小球能到达圆周轨道的最高点Q，且在Q点受到轻杆向下的拉力

D.小球能达到圆周轨道的最高点Q，且在Q点恰好不受轻杆的弹力

解析：设小球能到达Q点，且到达Q点时具有速度v，由机械能守恒得：

mv＝mg·2L+mv²

可解得：v＝0

在最高点，小球所需的向心力为零，故受轻杆向上的大小为mg的支持力.

答案：B

2.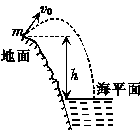如图所示，在地面上以速度v₀抛出质量为m的物体，抛出后物体落到比地面低h的海平面上.若以地面为零势能面且不计空气阻力，则下列说法中不正确的是(　)

A.物体到海平面时的重力势能为mgh

B.重力对物体做的功为mgh

C.物体在海平面上的动能为mv+mgh

D.物体在海平面上的机械能为mv

解析：以地面为参考平面，物体在海平面时的重力势能为－mgh，故A错误；抛出后的过程中机械能守恒，所以C、D正确；重力做功与路径无关，所以B正确.

答案：A

1.质量为m的物体由静止开始以2g的加速度竖直向下运动h高度.下列说法中正确的是(　)

A.物体的势能减少2mgh　B.物体的机械能保持不变

C.物体的动能增加2mgh　 D.物体的机械能增加mgh

解析：重力势能的减少量等于重力做的功，即ΔE_p＝mgh，A错误.

由题意知，物体除受重力外还受大小为mg的向下的作用力，机械能不守恒，B错误.

物体的合外力F_合＝2mg，故其动能的增量ΔE_k＝2mgh，C正确.

ΔE_p＝－mgh，ΔE_k＝2mgh，故ΔE＝ΔE_k+ΔE_p＝mgh，D正确.

答案：CD

13.(14分)一质量为m的皮球，无论从多高处自由落下，反弹高度都为原来的.要使皮球从h高处被拍打后，下落反弹回h高处，每次拍球需对球做的功为多少？(空气阻力不计)

错解：由于皮球反弹高度为原来的，说明皮球碰撞损失的能量为mgh.故每次拍球时需要对球做的功为mgh.

剖析：由题意知每次与地面碰撞损失的机械能为着地前机械能的，即若皮球从h高处自由释放，碰撞损失为：mgh，若皮球被W的功拍打后，着地碰撞损失大于mgh，故上面解析是错误的.

正解：设拍球时对球做功为W能使球反弹回h高处，由能的转化和守恒定律有：

W+mgh－(mgh+W)＝mgh

解得：W＝mgh.

答案：mgh

12.(13分)如图所示，在倾角为θ的斜面上，一物块通过轻绳的牵拉压紧弹簧.现将轻绳烧断，物块被弹出，与弹簧分离后即进入斜面上足够长的粗糙部分NN′(此前摩擦不计).物块沿斜面的粗糙部分上滑达到的最远位置离N的距离为s，此后下滑，第一次回到N处压缩弹簧后又被弹离，物块第二次上滑的最远位置离N的距离为.求：

(1)物块与粗糙斜面间的动摩擦因数μ.

(2)物块最终克服摩擦力做功所通过的路程s′.

解析：(1)设物块第一次下滑回到N时速度为v，则：

mgsin θ·s－μmgcos θ·s＝mv²

第二次上滑，初速度也为v，有：

mgsin θ·+μmgcos θ·＝mv²

联立解得：μ＝tan θ.

[或直接对动能为零的两个状态及过程运用动能定理：mgsin θ·－μmgcos θ·(s+)＝0，解得μ＝tan θ]

(2)物块进入NN′获得的初始动能为：

E_k0＝mgsin θ·s+μmgcos θ·s

物块最终只能在N点以下的斜面上往复运动，由动能定理有：

W_f＝μmgcos θ·s′

解得：s′＝4s.

答案：(1)tan θ　(2)4s

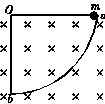
11.(13分)如图所示，半径为L的金属圆环ab竖直放置，磁感应强度为B的匀强磁场垂直纸面向里.金属轻杆Oa的a端连接质量为m的金属球，金属球可在金属圆环ab上自由滑动，现让Oa杆绕轴O由水平位置静止释放，运动中始终与固定的Ob杆组成闭合电路，经时间t金属球到达b处的速度为v(v＜).若Oa、Ob杆电阻均为R，其余电阻不计，则此过程中感应电动势的有效值为多少？

解析：根据能的转化和守恒定律，在Oa杆转至竖直方向的过程中，发生电磁感应转化的电能为：

W_电＝mgL－mv²

设这一过程感应电动势的有效值为E，有：

W_电＝·t

可解得：E＝.

答案：