
题目列表(包括答案和解析)
7.物体静止在光滑水平面上,先对物体施一水平向右的恒力F1,经时间t后撤去F1,立即再对它施加一水平向左的恒力F2,又经时间t后物体回到原出发点,在这一过程中,F1、F2分别对物体做的功W1、W2之比为多少?
6.设飞机飞行中所受阻力与其速度的平方成正比,若飞机以速度v匀速飞行,其发动机功率为P,则飞机以2v匀速飞行时,其发动机的功率为( )
A.2P B.4P C.8P D.无法确定
5.如图甲所示,滑轮质量、摩擦均不计,质量为2kg的物体在F作用下由静止开始向上做匀加速运动,其速度随时间的变化关系如图乙所示,由此可知( )(g取10m/s2)
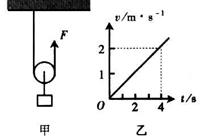
A.物体加速度大小为2 m/s2 B.F的大小为21N
C.4s末F的功率大小为42W D.4s内F做功的平均功率为42W
4.同一恒力按同样方式施于物体上,使它分别沿着粗糙水平地面和光滑水平抛面移动相同一段距离时,恒力的功和平均功率分别为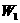 、
、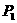 和
和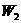 、
、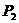 ,则二者的关系是( )
,则二者的关系是( )
A.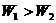 、
、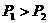 B.
B.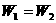 、
、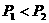
C.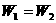 、
、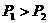 D.
D.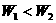 、
、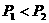
3.火车从车站开出作匀加速运动,若阻力与速率成正比,则( )
A.火车发动机的功率一定越来越大,牵引力也越来越大
B.火车发动机的功率恒定不变,牵引力也越来越小
C.当火车达到某一速率时,若要保持此速率作匀速运动,则发动机的功率这时应减小
D.当火车达到某一速率时,若要保持此速率作匀速运动,则发动机的功率一定跟此时速率的平方成正比
2.一质量为m的木块静止在光滑的水平面上,从t=0开始,将一个大小为F的水平恒力作用在该木块上,在t=T时刻F的功率是( )
A.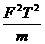 B.
B.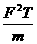 C.
C.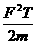 D.
D.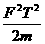
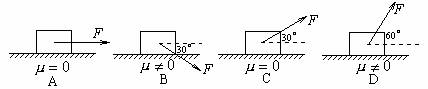
1.如图所示,力F大小相等,A B C D 物体运动的位移s也相同,哪种情况F做功最小( )
13. (14分)如图所示,在同一竖直平面内,一轻质弹簧静止放于光滑斜面上,其一端固定,另一端恰好与水平线AB平齐;长为L轻质细线一端固定在O点,另一端系一质量为m的小球,将细线拉至水平,此时小球在位置C.现由静止释放小球,小球到达最低点D时,细绳刚好被拉断,D点与AB相距h;之后小球在运动过程中恰好与弹簧接触并沿斜面方向压缩弹簧,弹簧的最大压缩量为x.试求:
(14分)如图所示,在同一竖直平面内,一轻质弹簧静止放于光滑斜面上,其一端固定,另一端恰好与水平线AB平齐;长为L轻质细线一端固定在O点,另一端系一质量为m的小球,将细线拉至水平,此时小球在位置C.现由静止释放小球,小球到达最低点D时,细绳刚好被拉断,D点与AB相距h;之后小球在运动过程中恰好与弹簧接触并沿斜面方向压缩弹簧,弹簧的最大压缩量为x.试求:
(1)细绳所能承受的最大拉力F.
(2)斜面的倾角θ.
(3)弹簧所获得的最大弹性势能Ep.
解析:(1)小球由C运动到D的过程机械能守恒,则有:
mgL=mv
解得:到D点时小球的速度v1=
在D点有:F-mg=m
解得:F=3mg
由牛顿第三定律知,细绳所能承受的最大拉力为3mg.
(2)小球由D运动到A的过程做平抛运动,由2gh=v,得在A点的竖直分速度vy=
故tan θ==
即斜面与水平所成的夹角θ=arctan .
(3)小球到达A点时,有:v=v+v=2g(h+L)
小球在压缩弹簧的过程中,小球与弹簧组成的系统机械能守恒,则有:
Ep=mgxsin θ+mv
故Ep=mg(x+h+L).
答案:(1)3mg (2)arctan
(3)mg(x+h+L)
12.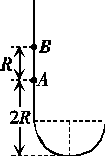 (13分)光滑的长轨道形状如图甲所示,底部为半圆形,其半径为R,固定在竖直平面内.A、B两质量相同的小环用长为R的轻杆连接在一起,套在轨道上.将A、B两环从图示位置静止释放,A环距离底端为2R.不考虑轻杆和轨道的接触,即忽略系统机械能的损失,求:
(13分)光滑的长轨道形状如图甲所示,底部为半圆形,其半径为R,固定在竖直平面内.A、B两质量相同的小环用长为R的轻杆连接在一起,套在轨道上.将A、B两环从图示位置静止释放,A环距离底端为2R.不考虑轻杆和轨道的接触,即忽略系统机械能的损失,求:
(1)A、B两环都未进入半圆形底部前,杆上的作用力.
(2)当A环下滑至轨道最低点时,A、B的速度大小.
解析:(1)两环都未进入半圆形轨道前都做自由落体运动,杆上的作用力为零.
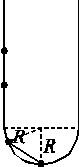 (2)当A环到达轨道最低点时,B环也已进入半圆轨道(如图乙所示),由几何关系知两环的速度大小相等,设为v,由机械能守恒定律得:
(2)当A环到达轨道最低点时,B环也已进入半圆轨道(如图乙所示),由几何关系知两环的速度大小相等,设为v,由机械能守恒定律得:
·2mv2=mg·2R+mg(2R+Rsin 30°)
解得:v=3.
答案:(1)两环都未进入半圆形轨道前都做自由落体运动,杆上的作用力为零
(2)A、B的速度大小均为3
11.(13分)如图所示,一固定在竖直平面内的光滑的半圆形轨道ABC,其半径R=0.5 m,轨道在C处与水平地面相切.在C处放一小物块,给它一水平向左的初速度v0=5 m/s,结果它沿CBA运动,通过A点,最后落在水平面上的D点,求C、D间的距离s.重力加速度g取 10 m/s2.[2006年高考·全国理综卷Ⅱ]
 解析:设小物块的质量为m,过A处时的速度为v,由A运动到D经历的时间为t,则有:
解析:设小物块的质量为m,过A处时的速度为v,由A运动到D经历的时间为t,则有:
mv=mv2+2mgR
2R=gt2
s=vt
联立解得:s=1 m.
答案:1 m
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com