1．标量和矢量

物理量分为两大类：凡是只须数值就能决定的物理量叫做标量；凡是既有大小，又需要方向才能决定的物理量叫做矢量。标量和矢量在进行运算是遵守不同的法则：标量的运算遵守代数法则；矢量的运算遵守平行四边形法则(或三角形法则)。

4．加速度

加速度是描述物体运动速度变化快慢的物理量，等于速度对时间的变化率，即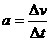，这样求得的加速度实际上是物体运动的平均加速度，瞬时加速度应为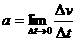。加速度是矢量。

3．瞬时速度和瞬时速率

瞬时速度是质点在某一时刻或经过某一位置是的速度，它定义为在时的平均速度的极限，简称为速度，即。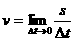

瞬时速度是矢量，它的方向就是平均速度极限的方向。瞬时速度的大小叫瞬时速率，简称速率。

2．平均速度和平均速率

平均速度是质点在一段时间内通过的位移和所用时间之比

，平均速度是矢量，方向与位移s的方向相同。

平均速率是质点在一段时间内通过的路程与所用时间的比值，是标量。

1．位置、位移和路程位置指运动质点在某一时刻的处所，在直角坐标系中，可用质点在坐标轴上的投影坐标(x,y,z)来表示。在定量计算时，为了使位置的确定与位移的计算一致，人们还引入位置矢量(简称位矢)的概念，在直角坐标系中，位矢r定义为自坐标原点到质点位置P(x,y,z)所引的有向线段，故有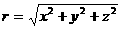,r的方向为自原点O点指向质点P，如图所示。

位移指质点在运动过程中，某一段时间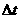内的位置变化，即位矢的增量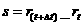，它的方向为自始位置指向末位置，如图所示，路程指质点在时间内通过的实际轨迹的长度。

2.一般的曲线运动：在一般的曲线运动中仍有法向力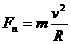式中R为研究处曲线的曲率半径，即在该处附近取一段无限小的曲线，并视为圆弧，R为该圆弧的曲率半径，即为研究处曲线的曲率半径。

[典型例题]

例题1：如图所示，以水平初速度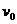抛出的物体，飞行一段时间后，垂直地撞在倾角为的斜面上，求物体完成这段飞行的时间是多少？

例题2：如果把上题作这样的改动：若让小球从斜面顶端A以水平速度抛出，飞行一段时间后落在斜面上的B点，求它的飞行时间为多少(已知)？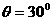

例题3：斜向上抛出一球，抛射角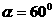,当t=1秒钟时，球仍斜向上升，但方向已跟水平成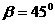角。(1)球的初速度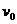是多少？(2)球将在什么时候达到最高点？

例题4：以v₀=10m/s的初速度自楼顶平抛一小球，若不计空气阻力，当小球沿曲线运动的法向加速度大小为5m/s时，求小球下降的高度及所在处轨迹的曲率半径R.

1.变速圆周运动

在变速圆周运动中，物体受到的合外力一般不指向圆心，这时合外力可以分解在法线(半径方向)和切线两个方向上。在法线方向有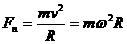充当向心力(即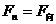)，产生的法向加速度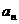只改变速度的方向；切向分力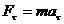产生的切向加速度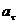只改变速度的大小。也就是说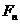，是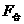的一个分力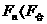，，且满足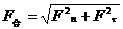

(1)定义：具有斜向上的初速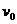且只受重力作用的物体的运动。

(2)性质：斜抛运动是加速度a=g的匀变速曲线运动。

(3)处理方法：正交分解法：将斜抛运动分解为水平方向的匀速直线运动和竖直方向的竖直上抛运动，然后用直角三角形求解。如图所示

(4)斜抛运动的规律如下：

任一时刻的速度　　　 ,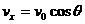

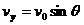　　　　　　　　　　 -gt.

任一时刻的位置　　　 ,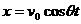

　　　　　　　　　　 .

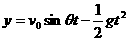竖直上抛运动、平抛运动可分别认为是斜抛运动在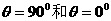时的特例.

斜抛运动在最高点时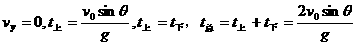

水平方向的射程斜抛物体具有最大的射程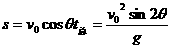

斜抛物体的最大高度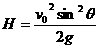

斜抛运动具有对称性，在同一段竖直位移上，向上和向下运动的时间相等；在同一高度上的两点处速度大小相等，方向与水平方向的夹角相等；向上、向下的运动轨迹对称。

2．开普勒三定律

[典型例题]

例题1：若地球为均匀的球体，在地球内部距地心距离为r的一物体m受地球的万有引力为多大？(已知地球的质量为M，半径为R)

例题2：一星球可看成质量均匀分布的球体，其半径为R，质量为M。假定该星球完全靠万有引力维系，要保证星球不散开，它自转的角速度不能超过什么限度？

例题3：(全国物理竞赛预赛题)已知太阳光从太阳射到地球需要8min20s，地球公转轨道可以近似看作圆轨道，地球半径约为6.4×10⁶m，试估算太阳质量M与地球质量m之比M/m为多大？(3×10⁵)

例题4：(全国物理竞赛预赛题)木星的公转周期为12年。设地球至太阳的距离为1AU(天文单位)，则木星至太阳的距离约为多少天文单位？(5.2AU)

例题5：世界上第一颗人造地球卫星的长轴比第二颗短8000km，第一颗卫星开始绕地球运转时周期为96.2min，求：

(1)第一颗人造卫星轨道的长轴。(1.39×10⁷m)

(2)第二颗人造卫星绕地球运转的周期。已知地球质量M=5.98×10²⁴kg。(191min)

1．均匀球壳的引力公式

由万有引力定律可以推出，质量为M、半径为R的质量均匀分布的球壳，对距离球心为r、质量为m的质点的万有引力为

F=0　　　　　　　 (r<R)

F=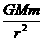　　　　　 (r>R)