7．物体平衡的种类

分为稳定平衡、不稳定平衡和随遇平衡三种类型。

稳度及改变稳度的方法：处于稳定平衡的物体，靠重力矩回复原来平衡位置的能力，叫稳度。降低重心高度、加大支持面的有效面积都能提高物体的稳度；反之，则降低物体的稳度。

[典型例题]

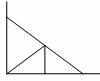
例题1：求如图所示中重为G的匀均质板(阴影部分)的重心O的位置。

例题2：求如图所示中的由每米长质量为G的7根匀质杆件构成的平面衍架的重心。

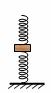
例题3：如图所示，均匀矩形物体的质量为m，两侧分别固定着轻质弹簧L₁和L₂，它们的劲度系数分别为k₁和k₂，先使L₂竖立在水平面上，此时L₁自由向上伸着，L₂被压缩。待系统竖直静止后，再对L₁的上端A施一竖直向上和力F，使L₂承受的压力减为重的3/4时，A端比加F之前上升的高度是多少？

例题4：图中的BO是一根质量均匀的横梁，重量G₁=80N。BO的一端安在B点，可绕通过B点且垂直于纸面的轴转动，另一端用钢绳AO拉着。横梁保持水平，与钢绳的夹角θ=30°。在横梁的O点挂一重物，重量G₂=240N。求钢绳对横梁的拉力F₁。

6．刚体的平衡

刚体：在任何情况下形状大小都不发生变化的力学研究对象。

力偶、力偶矩：二个大小相等、方向相反而不在一直线上的平行力称为力偶。力偶中的一个力与力偶臂(两力作用线之间的垂直距离)的乘积叫做力偶矩。在同一平面内各力偶的合力偶矩等于各力偶矩的代数和。

平衡条件：合力为零，即∑F=0；对任一转动轴合力矩为零，即∑M=0。

5．有固定转动轴物体的平衡

力矩：力F与力臂L的乘积叫做力对转动轴的力矩。即M=FL , 单位：N·m。

平衡条件：力矩的代数和为零。即M₁+M₂+M₃+……=0。

4．力的合成与分解

余弦定理：计算共点力F₁与F₂的合力F

F=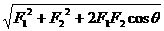

φ=arctan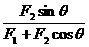(φ为合力F与分力F₁的夹角)

三角形法则与多边形法则：多个共点共面的力合成，可把一个力的始端依次画到另一个力的终端，则从第一个力的始端到最后一个力的终端的连线就表示这些力的合力。

拉密定理：三个共点力的合力为零时，任一个力与其它两个力夹角正弦的比值是相等的。

3．摩擦力

最大静摩擦力：可用公式F _m=μ₀F_N来计算。F_N为正压力，μ₀为静摩擦因素，对于相同的接触面，应有μ₀>μ(μ为动摩擦因素)

摩擦角：若令μ₀==tanφ，则φ称为摩擦角。摩擦角是正压力F_N与最大静摩擦力F _m的合力与接触面法线间的夹角。

2．弹力

胡克定律：在弹性限度内，弹力F的大小与弹簧伸长(或缩短)的长度x成正比，即F=k x，k为弹簧的劲度系数。

两根劲度系数分别为k₁，k₂的弹簧串联后的劲度系数可由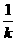=+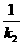求得，并联后劲度系数为k=k₁+k₂.

1．重力

物体的重心与质心

重心：从效果上看，我们可以认为物体各部分受到的重力作用集中于一点，这一点叫做物体的重心。

质心：物体的质量中心。

设物体各部分的重力分别为G₁、G₂……G_n，且各部分重力的作用点在oxy坐标系中的坐标分别是(x₁，y₁)(x₂，y₂)……(x_n，y_n),物体的重心坐标x_c，y_c可表示为

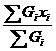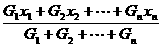x_c==，　 y_c==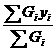

物体的运动是相对于参照系而言的，同一物体的运动相对于不同的参照系其运动情况不相同，这就是运动的相对性。我们通常把物体相对于基本参照系(如地面等)的运动称为“绝对运动”，把相对于基本参照系运动着的参照系称为运动参照系，运动参照系相对于基本参照系的运动称为“牵连运动”，而物体相对于运动参照系的运动称为“相对运动”。显然绝对速度和相对速度一般是不相等的，它们之间的关系是：绝对速度等于相对速度与牵连速度的矢量和。即

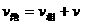或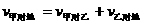

[典型例题]

例题1：A、B两车沿同一直线同向行驶。A车在前，以速度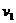做匀速直线运动；B车在后，先以速度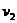做匀速直线运动(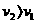)。当两车相距为d时(B车在后)，车开始做匀减速运动，加速度的大小为a。试问为使两车不至于相撞，d至少为多少?

例题2：河宽d=100m,水流速度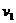=4m/s，船在静水中的速度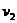=3m/s，要使航程最短，船应怎样渡河？

例题3：有A, B两球，A从距地面高度为h处自由下落，同时将B球从地面以初速度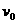竖直上抛，两球沿同一条竖直线运动。试分析：

(1)B球在上升过程中与A球相遇；

(2)B球在下落过程中与A球相遇。两种情况中B球初速度的取值范围。

定义：物体以初速度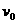向上抛出，不考虑空气阻力作用，这样的运动叫做竖直上抛运动。

2．运动的合成和分解

在研究物体运动时，将碰到一些较复杂的运动，我们常把它分解为两个或几个简单的分运动来研究。任何一个方向上的分运动，都按其本身的规律进行，不会因为其它方向的分运动的存在而受到影响，这叫做运动的独立性原理。运动的合成和分解包括位移、速度、加速度的合成和分解，他们都遵守平行四边形法则。