5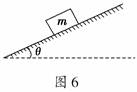．(2009·北京高考)如图6所示，将质量为m的滑块放在倾角　

为θ的固定斜面上．滑块与斜面之间的动摩擦因数为μ.若滑

块与斜面之间的最大静摩擦力和滑动摩擦力大小相等，重力

加速度为g，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．将滑块由静止释放，如果μ＞tanθ，滑块将下滑

B．给滑块沿斜面向下的初速度，如果μ＜tanθ，滑块将减速下滑

C．用平行于斜面向上的力拉滑块向上匀速滑动，如果μ＝tanθ，拉力大小应是2mgsinθ

D．用平行于斜面向下的力拉滑块向下匀速滑动，如果μ＝tanθ，拉力大小应是mgsinθ

解析：由μ＝tanθ条件可知μmgcosθ＝mgsinθ，即滑动摩擦力等于重力沿斜面向下的分力，在沿斜面向上的拉力作用下滑块匀速上滑，滑块沿斜面方向合力为零，即拉力F_拉＝mgsinθ+μmgcosθ＝2mgsinθ.C项正确．

答案：C

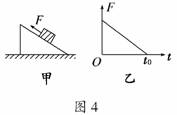
4．如图4甲所示，一物块放在粗糙斜面上，在平行斜面向上　

的外力F作用下斜面和物块始终处于静止状态，当F按图乙　

所示规律变化时，物块与斜面间的摩擦力大小变化规律可能

是图5中的　　　　　　　　　　　　　　　　　　 (　)

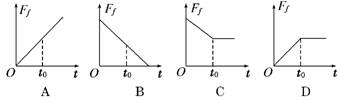
图5

解析：依题意，若静摩擦力的方向沿着斜面向上，则有F+F_f＝mgsinθ，在力F减小的过程中，F_f增大，直到力F减小到零时F_f恒定，则D可选；若静摩擦力的方向沿着斜面向下，则有F＝F_f+mgsinθ，在力F减小的过程中，F_f先减小到零，然后反向增大到mgsinθ恒定，无选项对应．

答案：D

3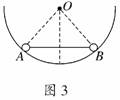．(2010·黄冈月考)如图3所示，质量为m的两个球A、B固定在杆的两端，将其放入光滑的半圆形碗中，杆的长度等于碗的半径，当杆与碗的竖直半径垂直时，两球刚好能平衡，则杆对小球的作用力为　　　　 (　)

A.mg　 　　　　B.mg　　　　　 C.mg　 　　　D．2mg

解析：由已知条件知，A、B间的杆一定水平，对其中一个小球受　　

力分析，由共点力的平衡知识可得，杆的作用力为F＝mgtan30°＝mg，故选项A正确．

答案：A

2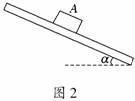．(2010·广州模拟)如图2所示，物块A放在倾斜的木板上，已知木板的倾角α分别为30°和45°时物块所受摩擦力的大小恰好相同，则物块和木板间的动摩擦因数为　　　　　　　 (　)

A. 　　　　B.　　　　　　 C. 　　　　　　　D.

解析：由题意可以推断出，当倾角α＝30°时，物体受到的摩擦力是静摩擦力，大小为F_f1＝mgsin30°，当α＝45°时，物体受到的摩擦力为滑动摩擦力，大小为F_f2＝μF_N＝μmgcos45°，由F_f1＝F_f2得μ＝.C项正确．

答案：C

1．(2008·山东高考)用轻弹簧竖直悬挂质量为m的物体，静止时弹簧伸长量为L.现用该弹簧沿斜面方向拉住质量为2m的物体，系统静止时弹簧伸长量也为L.斜面倾角为30°，如图1所示．则物体所受摩擦力　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．等于零

B．大小为mg，方向沿斜面向下

C．大小为mg，方向沿斜面向上

D．大小为mg，方向沿斜面向上

解析：由题意可知，kL＝mg，物体在斜面上静止时，设受到向上的静摩擦力F_f，由平衡条件得kL+F_f＝2mgsinθ，可得出F_f＝0，故选A.

答案：A

8．(2010·南京模拟)17世纪英国物理学家胡克发现：在弹性限度内，弹簧的形变量与弹力成正比，这就是著名的胡克定律．受此启发，一学习小组同学研究“金属线材伸长量与拉力的关系”的探究过程如下：

A．有同学认为：横截面为圆形的金属丝或金属杆在弹性限度内，其伸长量与拉力成正比，与截面半径成反比．

B．他们准备选用一些“由同种材料制成的不同长度、不同半径的线材”作为研究对象，用测距仪、传感器等仪器测量线材的伸长量随拉力变化的规律，以验证假设．

C．通过实验取得如下数据：

长度	拉力 　　　　 伸长 直径	250 N	500 N	750 N	1 000 N
1 m	2.52 mm	0.4 mm	0.8 mm	1.2 mm	1.6 mm
2 m	2.52 mm	0.8 mm	1.6 mm	2.4 mm	3.2 mm
1 m	3.57 mm	0.2 mm	0.4 mm	0.6 mm	0.8 mm

D．同学们对实验数据进行分析、归纳后，对他们的假设进行了补充完善．

(1)上述科学探究活动中，属于“制定计划”和“搜集证据”的环节分别是________、________.

(2)请根据上述过程分析他们的假设是否全部正确？若有错误或不足，请给予修正．

解析：确定研究对象，选取实验器材属“制定计划”；实验过程和测量数据属“搜集证据”．研究伸长量x与拉力F、长度L、直径D的关系时，采用控制变量法，比如长度、直径不变，再研究伸长量与力的关系，这种方法称为控制变量法．这是物理实验中的一个重要研究方法．

答案：(1)B　C　(2)他们的假设不是全部正确．在弹性限度内，金属丝(杆)的伸长量与拉力成正比，与截面半径的平方成反比，还与金属丝(杆)的长度成正比

7．橡皮筋也像弹簧一样，在弹性限度内，伸长量x与弹力F成正比，即F＝kx，k的值与橡皮筋未受到拉力时的长度L、横截面积S有关，理论与实践都表明k＝Y ，其中Y是一个由材料决定的常数，材料力学上称之为杨氏模量．

(1)在国际单位制中，杨氏模量Y的单位应该是　　　　　　　　　　　　　　 (　)

A．N　　　　　　 　B．m　　　　　　　　 C．N/m　　　　　 　D．Pa

　(2)有一段横截面是圆形的橡皮筋，应用如图实－2－14所示的实验装置可　

以测量出它的杨氏模量Y的值．首先利用测量工具a测得橡皮筋的长度L　

＝20.00 cm，利用测量工具b测得橡皮筋未受到拉力时的直径D＝4.000 　

mm，那么测量工具a应该是____________，测量工具b应该是

__________．

(3)下面的表格是橡皮筋受到的拉力F与伸长量x的实验记录.

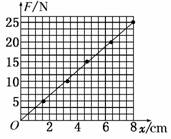
请作出F－x图象，由图象可求得该橡皮筋的劲度系数k＝________N/m.

(4)这种橡皮筋的Y值等于________．

解析：(1)在弹性限度内，弹力F与伸长量x成正比，F＝kx，又根据题意可知，k＝YS/L.

则F＝kx＝Y ·x

得出杨氏模量Y＝

各物理量取国际单位得杨氏模量的单位是N/m²＝Pa，选项D正确．

(2)根据精确度判断可知a为毫米刻度尺，b为螺旋测微器．

(3)根据表格数据，描点、连线，可得F－x图象如图所示．根据斜率的物量意义表示劲度系数k，

k＝≈3.1×10² N/m.

(4)根据Y＝kL/S求得，Y≈5×10⁶ Pa.

答案：(1)D　(2)毫米刻度尺　螺旋测微器　(3)图象见解析图　3.1×10²　(4)5×10⁶ Pa

6．(2008·北京高考)某同学和你一起探究弹力和弹簧伸长的关系，并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上，然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧，并使弹簧另一端的指针恰好落在刻度尺上．当弹簧自然下垂时，指针指示的刻度数值记作L₀；弹簧下端挂一个50 g的砝码时，指针指示的刻度数值记作L₁；弹簧下端挂两个50 g的砝码时，指针指示的刻度数值记作L₂；……；挂七个50 g的砝码时，指针指示的刻度数值记作L₇.

(1)下表记录的是该同学已测出的6个值，其中有两个数值在记录时有误，它们的代表符号分别是________________和______________.

(2)实验中，L₃和L₇两个值还没有测定，请你根据图实－2－13将这两个测量值填入上表中．

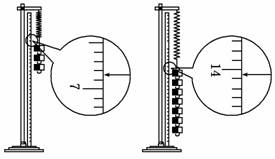
图实－2－13

(3)为了充分利用测量数据，该同学将所测得的数值按如下方法逐一求差，分别计算出了三个差值：d₁＝L₄－L₀＝6.90 cm，d₂＝L₅－L₁＝6.90 cm，d₃＝L₆－L₂＝7.00 cm.

请你给出第四个差值：d₄＝________＝________cm.

(4)根据以上差值，可以求出每增加50 g砝码的弹簧平均伸长量ΔL.ΔL用d₁、d₂、d₃、d₄表示的式子为：ΔL＝__________________________________________________，

代入数据解得ΔL＝________cm.

(5)计算弹簧的劲度系数k＝______________N/m.(g取9.8 m/s²)

解析：(1)L₅、L₆两组数据在读数时均没有估读值．

(2)根据表格已知读数，刻度尺上端的刻度数小，因而L₃＝6.85 cm，L₇＝14.05 cm.

(3)题中三组数据在寻求多挂4个砝码形成的长度差，故d₄＝L₇－L₃＝(14.05－6.85)cm＝7.20 cm.

(4)每增加4个砝码弹簧的平均伸长量ΔL₁＝，则每增加1个砝码弹簧的平均伸长量ΔL＝＝，代入数据求得ΔL＝1.75 cm.

(5)由(3)(4)可知，弹力F和弹簧伸长量ΔL成正比，即满足F＝kΔL，代入数据

k＝＝ N/m＝28 N/m.

答案：(1)L₅　L₆　(2)6.85　14.05

(3)L₇－L₃　7.20

(4)　1.75　(5)28

5．某同学用如图实－2－11所示装置做“探究弹力和弹簧伸长关系”的实验．他先测出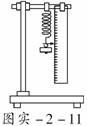不挂钩码时弹簧下端指针所指的标尺刻度，然后在弹簧下端挂上钩码，并逐个增加钩码，测出指针所指的标尺刻度，所得数据列表如下：(g取9.8 m/s²)

(1)根据所测数据，在图实－2－12所示的坐标纸上作出弹簧指针所指的标尺的刻度x与钩码质量m的关系曲线．

图实－2－12

(2)根据所测得的数据和关系曲线可以判断，在________N范围内弹力大小与弹簧伸长关系满足胡克定律，这种规格的弹簧的劲度系数为________N/m.

解析：(1)根据题目中所测量的数据进行描点，然后用平滑的曲线(或直线)连接各点，在连接时应让尽量多的点落在线上，偏差比较大的点舍去，不在线上的点尽量均匀分布在线的两侧，如图所示．

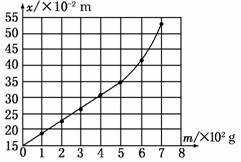
(2)根据所画图象可以看出，当m≤5.00×10² g＝0.5 kg时，标尺刻度x与钩码质量m成一次函数关系，所以在F≤4.9 N范围内弹力大小与弹簧伸长关系满足胡克定律，由胡克定律F＝kΔx可知，图线斜率的大小在数值上等于弹簧的劲度系数k，即

k＝＝＝25.0 N/m.

答案：(1)见解析　(2)0-4.9　25.0

4．用如图实－2－10甲所示的装置测定弹簧的劲度系数，被测弹簧一端固定于A点，另一端B用细绳绕过定滑轮挂钩码，旁边竖直固定一最小刻度为mm的刻度尺，当挂两个钩码时，绳上一定点P对应刻度如图实－2－10乙中ab虚线所示，再增加一个钩码后，P点对应刻度如图实－2－10乙中cd虚线所示，已知每个钩码质量为50 g，重力加速度g＝9.8 m/s²，则被测弹簧的劲度系数为________N/m.挂三个钩码时弹簧的形变量为________cm.

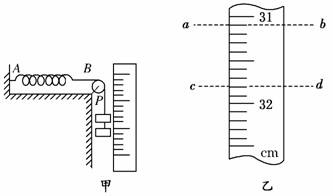
图实－2－10

解析：对钩码进行受力分析，根据平衡条件和胡克定律，得

2mg＝k(l－l₀)

3mg＝k(l′－l₀)

则k＝＝ N/m＝70 N/m

挂三个钩码时，可列方程

(m+m+m)g＝kΔx′

Δx′＝＝ m

＝2.10×10^－2 m＝2.10 cm.

答案：70　2.10