
题目列表(包括答案和解析)
34、如图31-1所示,从阴极K射出的电子经U0=5000V的电势差加速后,沿平行于板面的方向从中央射入两块长L1=10cm,间距d=4cm的平行金属板AB之间。在离金属板边缘L2=75cm处放置一个直径D=20cm,带有记录纸的圆筒。整个装置放在真空内,电子发射的初速度不计。
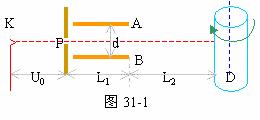
(1)若在金属板上加以U1=1000V的直流电压(A板电势高)后,为使电子沿入射方向作匀速直线运动到达圆筒,应加怎样的磁场(大小和方向);
(2)若在两金属板上加以U2=1000cos2πtV的交流电压,并使圆筒绕中心轴按图示方向以n=2转/秒匀速转动。试确定电子在记录纸上的轨迹形状,并画出1秒钟内所记录到的图形。
分析与解:偏转极板上加恒定电压 U后,电子在电场中受到恒定的电场力作用,故所加的磁场方向只要使运动电子所受到的洛仑兹力与电场力等大反向即可。偏转极板上加上正弦交流电后,板间电场变为交变电场,电子在板间的运动是水平方向作匀速直线运动,竖直方向作简谐运动。偏出极板后作匀速直线运动,电子到达圆筒后,在筒上留下的痕迹是电子在竖直方向的“扫描”和圆筒匀速转动的合运动。
据动能定理:eU0=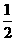 mV02,得电子加速后的入射速度为:
mV02,得电子加速后的入射速度为:
V0= =4.2×107m/s
=4.2×107m/s
(1)加直流电压时,A、B两板间场强:
E1=U1/d=1000/(4×10-2)=2.5×104v/m
为使电子作匀速直线运动,应使电子所受电场力与洛仑兹力平衡,即:qE1=qBV0,
得:B=E1/V0=(2.5×104)/(4.2×107)=6×10-4T
方向为垂直于纸面向里。
(2)加上交流电压时,A、B两板间场强为:
E2=U2/d=1000cos2πt/(4×10-2)=2.5×104cos2πt v/m
电子飞离金属板时的偏距为:y1=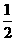 at12=
at12=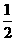 (eE2/m)(L1/V0)2
(eE2/m)(L1/V0)2
电子飞离金属板时的竖直速度为:Vy=at1=(eE2/m)(L1/V0)
从飞离板到到达筒的偏距:y2=Vyt2=(eE2/m)(L1/V0)(L2/V0)=(eE2L1L2)/(mV02)
所以在纸筒上的落点对入射方向的总偏距为:(如图31-2所示)

y=y1+y2=(L1/2+L2)(eE2L1/mV02)=(L1/2+L2)(L1U2/2U0d)
=(10/2+75)×10-2×(10×1000cos2πt)/(2×5000×4)=0.20cos2πt m
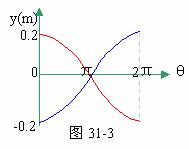
可见,在记录纸上的点以振幅0.20m,周期T=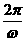 =1秒而作简谐运动。因圆筒每秒转2周(半秒转1周),故在1秒内,纸上的图形如图31-3所示。
=1秒而作简谐运动。因圆筒每秒转2周(半秒转1周),故在1秒内,纸上的图形如图31-3所示。
33、如图30-1所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感强度相同的匀强磁场,方向垂直纸面向外。ab是一根长L的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上。将一套在杆上的举正电小球从a端由静止释放后,小球先是加速运动,后是匀速运动则达b端。已知小球与绝缘杆间的动因摩擦数μ=0.3,小球的重力可忽略不计。当小球脱离杆进入虚线下方后,运动轨迹是半圆,圆半径为L/3。求:带电小球以 a到b运动过程中克服摩擦力做的功与电场力所做功的比值。
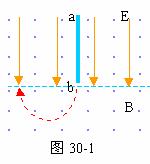
分析与解:(1)带电小球在沿杆向下运动时,其受力情况如30-2图示。

水平方向:F洛=N=qBV [1]
竖直方向:qE=f [2] (匀速运动时)
又因f=μN [3],联立解[1][2][3]式得:qE=f=μqBVb
小球在磁场中作匀速圆周运动:qBVb=mVb2/R=3mVb2/L,所以Vb=qBL/3m
小球从a到b运动过程中,由动能定理:W电-Wf=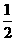 mVb2
mVb2
W电=qEL=μqBVbL=0.3×qBL(qBL/3m)=q2B2L2/10m
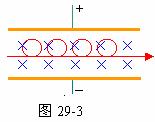
所以,Wf=W电-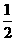 mVb2=q2B2L2/10m-(m/2)(q2B2L2/9m2)=2q2B2L2/45m
mVb2=q2B2L2/10m-(m/2)(q2B2L2/9m2)=2q2B2L2/45m
所以,Wf/W电=(2q2B2L2/45m)/(q2B2L2/10m)=4/9。
32、平行金属,板长1.4米,两板相距30厘米,两板间匀强磁场的B为1.3×10-3特斯拉,两板间所加电压随时间变化关系如29-1图所示。当t=0时,有一个a粒子从左侧两板中央以V=4×103米/秒的速度垂直于磁场方向射入,如29-2图所示。不计a粒子的重力,求:该粒子能否穿过金属板间区域?若不能,打在何处?若能,则需多长时间? (已知a粒子电量q=3.2×10-19库,质量m=6.64×10-27千克)
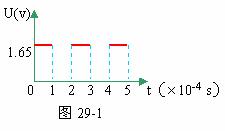
分析与解:在t=0到t=1×10-4秒时间内,两板间加有电压,a粒子受到电场力和洛仑兹力分别为:F=qu/d=q×1.56/0.3=5.2q 方向竖直向下
f=qBv=q×1.3×10-3×4×103=5.2q 方向竖直向上
因F=f,故做匀速直线运动,其位移为:△S=v△t=4×103×1×10-4=0.4米
在t=1×10-4秒到t=2×10-4秒时间内,两板间无电场,a粒子在洛仑兹力作用下做匀速圆周运动,其轨迹半径为:
r=mv/qB=(6.64×10-27×4×103)/(3.2×10-19×1.3×10-3)=6.37×10-2米<d/4
所以粒子不会与金属板相碰。面a粒子做匀速圆周运动的周期为:
T=2πm/qB=(2×3.14×6.64×10-27)/(3.2×10-19×1.3×10-3)=1.0×10-4秒
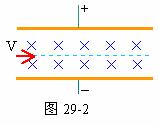
则在不加电压的时间内,a粒子恰好能在磁场中运动一周。当两板间又加上第2个周期和第3个周期的电压时,a粒子将重复上述的运动。故经13/4周期飞出板外(t=6.5×10-4秒)其运动轨迹如29-3图所示。
31、如图28-1所示,X轴上方有匀强磁场B,下方有匀强电场E。电量为q、质量为m、重力不计的粒子y轴上。X轴上有一点N(L.0),要使粒子在y轴上由静止释放而能到达N点,问:
(1)粒子应带何种电荷?
(2)释放点M应满足什么条件?
(3)粒子从M点运动到N点经历多长的时间?
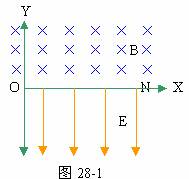
分析与解:(1) 粒子由静止释放一定要先受电场力作用 (磁场对静止电荷没有作用力),所以 M点要在-Y轴上。要进入磁场必先向上运动,静上的电荷要向上运动必须受到向上的电场力作用,而场强 E方向是向下的,所以粒子带负电。
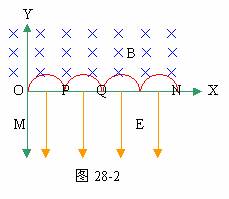
(2)粒子在M点受向上电场力,从静止出发做匀加速运动。在 O点进入匀强磁场后,只受洛仑兹力(方向沿+X轴)做匀速周围运动,经半个周期,回到X轴上的P点,进入匀强电场,在电场力作用下做匀减速直线运动直到速度为零。然后再向上做匀加速运动,在X轴上P点进入匀强磁场,做匀速圆运动,经半个周期回到X轴上的Q点,进入匀强电场,再在电场力作用下做匀减速运动直到速度为零。此后,粒子重复上述运动直到 X轴上的N点,运动轨迹如图28-2所示。
设释放点M的坐标为(0.-yO),在电场中由静止加速,则:qEyO=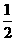 mV2 [1]
mV2 [1]
在匀强磁场中粒子以速率V做匀速圆周运动,有:qBV=m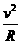 [2]
[2]
设n为粒子做匀速圆周运动的次数(正整数)则:L=n2R,所以R= [3]
[3]
解[1][2][3]式得:V=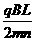 ,所以yO=
,所以yO=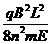 (式中n为正整数)
(式中n为正整数)
(3)粒子由M运动到N在电场中的加速运动和减速运动的次数为(2n-1)次,
每次加速或减速的时间都相等,设为t1,则:yO=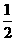 at12=
at12=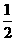 qEt12/m
qEt12/m
所以t1=
粒子在磁场中做匀速圆周运动的半周期为t2,共n次,t2=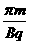
粒子从M点运动到N点共经历的时间为:
t=(2n-1)t1+nt2=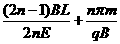 (n=1、2、3……)
(n=1、2、3……)
46.如图42-1所示为一固定在水平面上长L的绝缘板,整个空间有一水平的匀强电场,板在右半部有一个垂直于纸面向外的匀强磁场.一质量为m、带电量为q的物体,从板的P端由静止开始在电场力的作用下向右运动.小物体与水平面间摩擦系数为μ,进入磁场区域后恰能作匀速运动.当物体碰到挡板Q后被弹回.若在碰撞瞬间撤去电场,物体返回时在磁中仍能作匀速运动,离开磁场后作匀减速运动,并停在C点.设PC=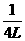 .求:
.求:
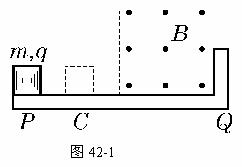
(1)物体与挡板碰撞前后的速率v1和v2;
(2)磁感应强度B的大小;
(3)电场强度E的大小和方向.
解 物体从P静止开始运动进入磁场速度v1,由动能定理得

进入磁场匀速,由反弹后仍匀速可知,电荷带正电.电场强度方向水平向右;进入磁场匀速
qE=μ(mg+qv1B),
反弹后匀速
mg=qv2B
出磁场后到C点停止
 ;
;
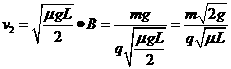
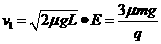 ,方向水平向右。
,方向水平向右。
45.现有一电阻箱,一个开关,若干根导线和一个电流表,该电流表表面上有刻度但无刻度值,要求设计一个能测定某电源内阻的实验方案(已知电流表内阻可忽略,电流表量程符合要求,电源内阻约为几欧).
要求:①画出实验电路图;
②简要写出完成接线后的实验步骤;
③写出用测得的量计算电源内阻的表达式r= .
答案:(1)图略 (2)①使电阻箱阻值最大,合上开关S,调节电阻箱阻值为R1,记下电流表对应的刻度N1;②调节电阻箱阻值为R2,记下电流表对应的刻度N2;③计算出r的值;④多侧几次;取r的平均值;⑤断开S,拆除电阻,整理器材.(3)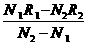 。
。
44.用长度相同,横截面积之比为2∶1的均匀铜导线制成的两个正方形线框M和N,使它们从同一高度自由下落,途中经过一个有边界的匀强磁场区域,磁场方向垂直纸面向里,如图41-1所示.若下落过程中线框平面始终与磁场方向保持垂直,不计空气阻力,则M、N底边进入磁场瞬间的速度vM∶vN= ,加速度aM∶aN= ,在穿过磁场的过程中,线框M、N内产生的热量QM∶QN= .
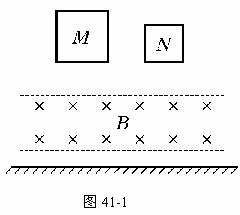
(答案:1:1,1:1,2:1)
43.密立根油滴实验如图40-1所示:在电介质为空气的电容器中,观测以某速度送入的一个油滴,这油滴经过一会儿达到一个恒定的速度v1,这时加上电场强度为E的匀强电场,再过一会儿达到另一恒定速度v2.在这样短的时间内速度变为恒定,说明油滴受到 的作用,这个力的大小与速度成正比,可表示为kv(式中k为常量)而方向与 .设油滴质量为m,电量为q,写出这两种情况下的方程式① ;② .
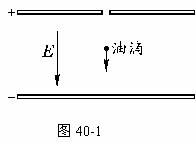
下面的表是通过这样的实验所测得的不同油滴所带电量q值的一个实例:q的测定值(单位:10-19C)
|
6.41 |
8.01 |
9.65 |
11.23 |
11.83 |
14.48 |
分析这些数据可知:
(答案.空气阻力 速度方向相反 ①mg-kv1=0 ②mg-kv 2-qE=0小球的电量是1.6×10-19C的整数倍,故电荷的最小电量为1.6×10-19C)
42.如图39-1所示,U型线框abcd处于匀强磁场中,磁场的磁感强度为B,方向垂直于纸面向内.长度为L的直导线MN中间串有一个电压表跨接在ab与cd上且与ab垂直,它们之间的接触是完全光滑的.R为电阻,C为电容器,现令MN以速度v0向右匀速运动,用U表示电压表的读数,q表示电容器所带电量,C表示电容器电容.F表示对MN的拉力.设电压表体积很小,其中线圈切割磁感线对MN间的电压的影响可以忽略不计.则[ ]
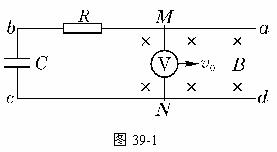
A.U=BLv0 F=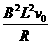
B.U=BLv0 F=0
C.U=0 F=0
D.U=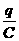 F=
F=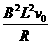
答案:C
41.如图38-1所示,三平行金属板a、b、c接到电动势分别为 、
、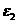 的电源上,已知
的电源上,已知 <
<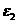 ,在A孔右侧有一带负电的质点,由静止释放后向右运动穿过B到达P点后再返回A孔,则[ ]
,在A孔右侧有一带负电的质点,由静止释放后向右运动穿过B到达P点后再返回A孔,则[ ]
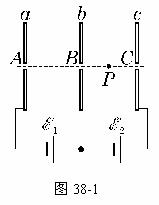
A.只将b板右移一小段距离后再释放该质点,质点仍运动到P点后返回
B.只将b板右移一小段距离后再释放该质点,质点将达不到P点
C.只将b板右移稍长距离后再释放该质点,质点能穿过C孔
D.若将质点放在C孔左侧由静止释放,质点将能穿过A孔
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com