
题目列表(包括答案和解析)
3.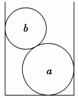 (2009·海南高考)两刚性球a和b的质量分别为ma和mb,
(2009·海南高考)两刚性球a和b的质量分别为ma和mb,
直径分别为da和db(da>db).将a、b球依次放入一竖直放
置、内径为d(da<d<da+db)的平底圆筒内,如图3所示.
设a、b两球静止时对圆筒侧面的压力大小分别为FN1和
FN2,筒底所受的压力大小为F.已知重力加速度大小为g. 图3
若所有接触都是光滑的,则 ( )
A.F=(ma+mb)g,FN1=FN2
B.F=(ma+mb)g,FN1≠FN2
C.mag<F<(ma+mb)g,FN1=FN2
D.mag<F<(ma+mb)g,FN1≠FN2

解析:对a和b整体受力分析如图所示,由平衡条件可知,
F=(ma+mb)g
FN1=FN2,故A正确.
答案:A
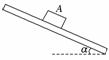
2.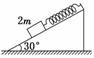 (2008·山东高考)用轻弹簧竖直悬挂质量为m的物体,静止时弹簧伸长量为L.现用该弹簧沿斜面方向拉住质量为2m的物体,系统静止时弹簧伸长量也为L.斜面倾角为30°,如图2所示.则物体所受摩擦力
( )
(2008·山东高考)用轻弹簧竖直悬挂质量为m的物体,静止时弹簧伸长量为L.现用该弹簧沿斜面方向拉住质量为2m的物体,系统静止时弹簧伸长量也为L.斜面倾角为30°,如图2所示.则物体所受摩擦力
( )
A.等于零
B.大小为mg,方向沿斜面向下 图2
C.大小为mg,方向沿斜面向上
D.大小为mg,方向沿斜面向上
解析:由题意可知,kL=mg,物体在斜面上静止时,设受到向上的静摩擦力Ff,由平衡条件得kL+Ff=2mgsinθ,可得出Ff=0,故选A.
答案:A
1.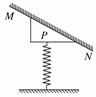 如图1所示,竖直放置的轻弹簧一端固定在地面上,
如图1所示,竖直放置的轻弹簧一端固定在地面上,
另一端与斜面体P连接,P的斜面与固定挡板MN
接触且处于静止状态,则斜面体P此刻所受的外力
个数有可能为 ( )
A.2个 B.3个 图1
C.4个 D.5个
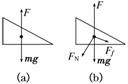 解析:若斜面体P受到的弹簧弹力F等于其重力mg,
解析:若斜面体P受到的弹簧弹力F等于其重力mg,
则MN对P没有力的作用,如图(a)所示,P受到2个
力,A对;若弹簧弹力大于P的重力,则MN对P有压
力FN,只有压力FN则P不能平衡,一定存在向右的力,
只能是MN对P的摩擦力Ff,因此P此时受到4个力,如图(b)所示,C对.
答案:AC
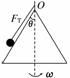
12.(2010·青岛模拟)如图13所示,一根长0.1 m的细线,一端系着一个质量为0.18 kg的小球,拉住线的另一端,使小球在光滑的水平桌面上做匀速圆周运动,使小球的转速很缓慢地增加,当小球的转速增加到开始时转速的3倍时,细线断开,线断开前的瞬间线受到的拉力比开始时大40 N,求:
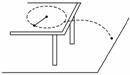
图13
(1)线断开前的瞬间,线受到的拉力大小;
(2)线断开的瞬间,小球运动的线速度;
(3)如果小球离开桌面时,速度方向与桌边缘的夹角为60°,桌面高出地面0.8 m,求小球飞出后的落地点距桌边缘的水平距离.
解析:(1)线的拉力提供小球做圆周运动的向心力,设开始时角速度为ω0,向心力为F0,线断开的瞬间,角速度为ω,线的拉力为FT.
F0=mω02R ①
FT=mω2R ②
由①②得== ③
又因为FT=F0+40 N ④
由③④得FT=45 N
(2)设线断开时小球的线速度为v,由FT=得,
v= = m/s=5 m/s
(3)设桌面高度为h,小球落地经历时间为t,落地点与飞出桌面点的水平距离为s.
由h=gt2得
t= =0.4 s
s=vt=2 m
则小球飞出后的落地点到桌边缘的水平距离为
l=ssin60°=1.73 m.
答案:(1)45 N (2)5 m/s (3)1.73 m
11.(2009·广东高考)如图12所示,一个竖直放置的圆锥筒可绕其中心轴OO′转动,筒内壁粗糙,筒口半径和筒高分别为R和H,筒内壁A点的高度为筒高的一半.内壁上有一质量为m的小物块.求:
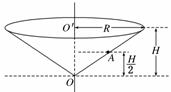
图12
(1)当筒不转动时,物块静止在筒壁A点受到的摩擦力和支持力的大小;
(2)当物块在A点随筒做匀速转动,且其所受到的摩擦力为零时,筒转动的角速度.
解析:(1)物块静止时,对物块进行受力分析如图所示,设筒壁与水平面的夹角为θ.
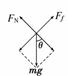 由平衡条件有
由平衡条件有
Ff=mgsinθ FN=mgcosθ
由图中几何关系有
cosθ= ,sinθ=
故有Ff=, FN=
(2)分析此时物块受力如图所示,
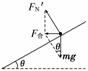 由牛顿第二定律有
由牛顿第二定律有
mgtanθ=mrω2.
其中tanθ=,r=,
可得ω= .
答案:(1) (2)
10.如图11所示,把一个质量m=1 kg的物体通过两根等长的细绳与
竖直杆上A、B两个固定点相连接,绳a、b长都是1 m,杆AB长度
是1.6 m,直杆和球旋转的角速度等于多少时,b绳上才有张力?
解析:如图所示,a、b两绳都伸直时,已知a、b绳长均为1 m,即 图11
==1 m,==0.8 m
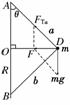 在△AOD中,cosθ===0.8
在△AOD中,cosθ===0.8
sinθ=0.6,θ=37°
小球做圆周运动的轨道半径
r==·sinθ=1×0.6 m=0.6 m.
b绳被拉直但无张力时,小球所受的重力mg与a绳拉力FTa的合力F为向心力,其受力分析如图所示,由图可知小球的向心力为
F=mgtanθ
根据牛顿第二定律得
F=mgtanθ=mr·ω2
解得直杆和球的角速度为
ω== rad/s≈3.5 rad/s.
当直杆和球的角速度ω>3.5 rad/s时,b中才有张力.
答案:ω>3.5 rad/s
9.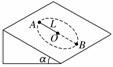 (2010·湖南三十二校模拟)如图10所示,在倾角α=30°的光滑斜
(2010·湖南三十二校模拟)如图10所示,在倾角α=30°的光滑斜
面上,有一根长为L=0.8 m的细绳,一端固定在O点,另一端
系一质量为m=0.2 kg的小球,小球沿斜面做圆周运动.若要小
球能通过最高点A,则小球在最低点B的最小速度是 ( ) 图10
A.2 m/s B.2 m/s
C.2 m/ s D.2 m/s
 解析:通过A点的最小速度为vA==2
m/s,则根据机械能守恒定律得:mvB2=mvA2+mgL,解得vB=2
m/s,即C选项正确.
解析:通过A点的最小速度为vA==2
m/s,则根据机械能守恒定律得:mvB2=mvA2+mgL,解得vB=2
m/s,即C选项正确.
答案:C
8.(2010·山东省青岛三中月考)用一根细线一端系一小球(可视为质点),另
一端固定在一光滑锥顶上,如图8所示,设小球在水平面内做匀速圆周
运动的角速度为ω,细线的张力为FT,则FT随ω2变化的图象是图9
中的 ( ) 图8

图9
解析:小球角速度ω较小,未离开锥面对,设细线的张力为FT,线的长度为L,锥面对小球的支持力为FN,则有FTcosθ+FNsinθ=mg,FTsinθ-FNcosθ=mω2Lsinθ,可得出:FT=mgcosθ+mω2Lsin2θ,可见随ω由0开始增加,FT由mgcosθ开始随ω2的增大,线性增大,当角速度增大到小球飘离锥面时,FT·sinα=mω2Lsinα,得FT=mω2L,可见FT随ω2的增大仍线性增大,但图线斜率增大了,综上所述,只有C正确.
答案:C
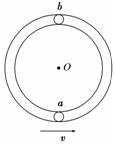
7.(2010·长沙五校联考)如图7所示光滑管形圆轨道半径为R(管径远小
于R),小球a、b大小相同,质量均为m,其直径略小于管径,能
在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当
小球a在最低点时,小球b在最高点,以下说法正确的是( )
A.当小球b在最高点对轨道无压力时,小球a比小球b所需向心
力大5mg 图7
B.当v=时,小球b在轨道最高点对轨道无压力
C.速度v至少为,才能使两球在管内做圆周运动
D.只要v≥,小球a对轨道最低点的压力比小球b对轨道最高点的压力大6mg
解析:小球在最高点恰好对轨道没有压力时,小球b所受重力充当向心力,mg=m⇒v0=,小球从最高点运动到最低点过程中,只有重力做功,小球的机械能守恒,2mgR+mv02=mv2,解以上两式可得:v=,B项正确;小球在最低点时,F向=m=5mg,在最高点和最低点所需向心力的差为4mg,A项错;小球在最高点,内管对小球可以提供支持力,所以小球通过最高点的最小速度为零,再由机械能守恒定律可知,2mgR=mv′2,解得v′=2,C项错;当v≥时,小球在最低点所受支持力F1=mg+,由最低点运动到最高点,2mgR+mv12=mv2,小球对轨道压力F2+mg=m,解得F2=m-5mg,F1-F2=6mg,可见小球a对轨道最低点压力比小球b对轨道最高点压力大6mg,D项正确.
 答案:BD
答案:BD
6.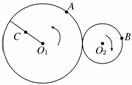 如图6所示,靠摩擦传动做匀速转动的大、小两轮接触面互
如图6所示,靠摩擦传动做匀速转动的大、小两轮接触面互
不打滑,大轮半径是小轮半径的2倍.A、B分别为大、小轮
边缘上的点,C为大轮上一条半径的中点.则( )
A.两轮转动的角速度相等
B.大轮转动的角速度是小轮的2倍 图6
C.质点加速度aA=2aB
D.质点加速度aB=4aC
解析:两轮不打滑,边缘质点线速度大小相等,vA=vB,而rA=2rB,故ωA=ωB,A、B错误;由an=得==,C错误;由an=ω2r得==2,则=4,D正确.
 答案:D
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com