
题目列表(包括答案和解析)
35.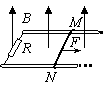 湖南省雅礼中学2010届高三上学期第五次月考如图所示,足够长的水平导体框架的宽度L=0.5 m,电阻忽略不计,定值电阻R=2Ω。磁感应强度B=0.8 T的匀强磁场方向垂直于导体框平面,一根质量为m=0.2
kg、有效电阻r=2Ω的导体棒MN垂直跨放在框架上,该导体棒与框架间的动摩擦因数μ=0.5,导体棒在水平恒力F=1.2N的作用下由静止开始沿框架运动到刚开始匀速运动时,通过导体棒截面的电量共为q=2 C,求:
湖南省雅礼中学2010届高三上学期第五次月考如图所示,足够长的水平导体框架的宽度L=0.5 m,电阻忽略不计,定值电阻R=2Ω。磁感应强度B=0.8 T的匀强磁场方向垂直于导体框平面,一根质量为m=0.2
kg、有效电阻r=2Ω的导体棒MN垂直跨放在框架上,该导体棒与框架间的动摩擦因数μ=0.5,导体棒在水平恒力F=1.2N的作用下由静止开始沿框架运动到刚开始匀速运动时,通过导体棒截面的电量共为q=2 C,求:
(1)导体棒做匀速运动时的速度;
(2)导体棒从开始运动到刚开始匀速运动这一过程中,导体棒产生的电热。
(g取10 m/s2)
解:(1)当物体开始做匀速运动时,有: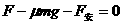 (1分)
(1分)
又 :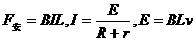 (2分)
(2分)
解得 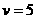 m/s
(1分)
m/s
(1分)
(2) 设在此过程中MN运动的位移为x,则
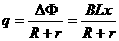 解得:
解得: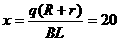 m (1分)
m (1分)
设克服安培力做的功为W,则:
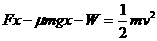 解得:W=1.5J
(2分)
解得:W=1.5J
(2分)
所以电路产生的总电热为1.5J,导体棒产生的电热为0.75J (1分)
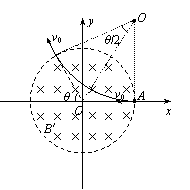
34.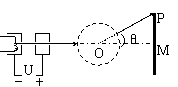 山东省潍坊市2010届高三上学期阶段性测试电视机的显像管中,电子束的偏转是用磁偏转技术实现的.电子束经过电压为U的加速电场后,进入一圆形匀强磁场区,如图所示.磁场方向垂直于圆面.磁场区的中心为O,半径为r.当不加磁场时,电子束将通过O点而打到屏幕的中心M点.为了让电子束射到屏幕边缘P,需要加磁场,使电子束偏转一已知角度θ,此时磁场的磁感应强度B应为多少?(电子荷质比为e/m,重力不计)
山东省潍坊市2010届高三上学期阶段性测试电视机的显像管中,电子束的偏转是用磁偏转技术实现的.电子束经过电压为U的加速电场后,进入一圆形匀强磁场区,如图所示.磁场方向垂直于圆面.磁场区的中心为O,半径为r.当不加磁场时,电子束将通过O点而打到屏幕的中心M点.为了让电子束射到屏幕边缘P,需要加磁场,使电子束偏转一已知角度θ,此时磁场的磁感应强度B应为多少?(电子荷质比为e/m,重力不计)
解:电子加速时,有:eU=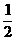 mv2
(2分)
mv2
(2分)
在磁场中,有:evB=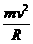 (2分)
(2分)
由几何关系,有:tan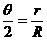 (2分)
(2分)
由以上各式解得:B=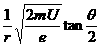 (2分)
(2分)
33.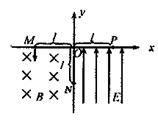 福建省龙岩二中2010届高三摸底考试如图所示,在x<0且y<0的区域内存在匀强磁场,磁场方向垂直于xy平面向里.磁感应强度大小为B,在x>0且y<0的区域内存在沿y轴正方向的匀强电场. 一质量为m、电荷量为q的带电粒子从x轴上的M点沿y轴负方向垂直射入磁场,结果带电粒子从y轴的N点射出磁场而进入匀强电场,经电场偏转后打到x轴上的P点,已知
福建省龙岩二中2010届高三摸底考试如图所示,在x<0且y<0的区域内存在匀强磁场,磁场方向垂直于xy平面向里.磁感应强度大小为B,在x>0且y<0的区域内存在沿y轴正方向的匀强电场. 一质量为m、电荷量为q的带电粒子从x轴上的M点沿y轴负方向垂直射入磁场,结果带电粒子从y轴的N点射出磁场而进入匀强电场,经电场偏转后打到x轴上的P点,已知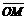 =
=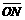 =
=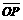 =l。不计带电粒子所受重力,求:
=l。不计带电粒子所受重力,求:
(1)带电粒子进入匀强磁场时速度的大小;
(2)带电粒子从射入匀强磁场到射出匀强电场所用的时间;
(3)匀强电场的场强大小.
解:(1)设带电粒子射入磁场时的速度大小为v,由带电粒子射入匀强磁场的方向和几何关系可知,带电粒子在磁场中做圆周运动,圆心位于坐标原点,半径为l。
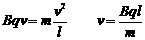
(2)设带电粒子在磁场中运动时间为t1,在电场中运动的时间为t2,总时间为t。
t1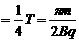 t2
t2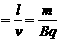
t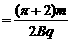
(3)带电粒子在电场中做类平抛运动
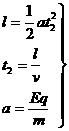 所以
所以
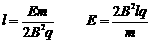
32.广东省蓝田中学2010届高三摸底考试如图所示,宽度为L的足够长的平行金属导轨MN、PQ的电阻不计,垂直导轨水平放置一质量为m电阻为R的金属杆CD,整个装置处于垂直于导轨平面的匀强磁场中,导轨平面与水平面之间的夹角为θ,金属杆由静止开始下滑,动摩擦因数为μ,下滑过程中重力的最大功率为P,求磁感应强度的大小.
解:金属杆先加速后匀速运动,设匀速运动的速度为v,此时有最大功率,金属杆的电动势为:E=BLv)
 回路电流 I =
回路电流 I =
安培力 F = BIL
金属杆受力平衡,则有:mgsinθ= F + μmgcosθ
重力的最大功率P = mgvsinθ (1分)
解得:B =
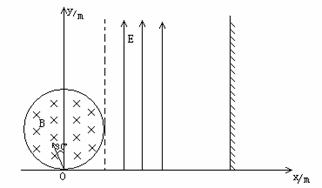
31.福建省泉州市四校2010届高三上学期期末联考如图为某一装置的俯视图,PQ、MN为竖直放置的很长的平行金属薄板,两板间有匀强磁场,它的磁感应强度大小为B,方向竖直向下。金属棒AB搁置在两板上缘,与两板垂直且接触良好,当AB棒在两板上运动时,有一个质量为m、带电量为+q、重力不计的粒子,从两板中间(到两板距离相等)以初速度v0平行MN板射入,并恰好做匀速直线运动。问:
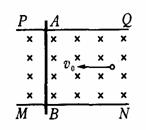 (1)金属棒AB的速度大小与方向如何?
(1)金属棒AB的速度大小与方向如何?
(2)若金属棒运动突然停止(电场立即消失),带电粒子在磁场中运动一段时间,然后撞在MN上,且撞击MN时速度方向与MN板平面的夹角为450 。则PQ与MN板间的距离大小可能是多少?从金属棒AB停止运动到粒子撞击MN板的时间可能是多长?
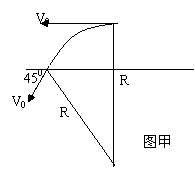 解析:(1)由左手定则,+q受洛伦兹力方向垂直指向板MN,则电场方向垂直指向板PQ,据右手定则,可知棒AB向左运动。
解析:(1)由左手定则,+q受洛伦兹力方向垂直指向板MN,则电场方向垂直指向板PQ,据右手定则,可知棒AB向左运动。
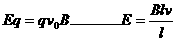 ,求得.
,求得.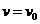 。(4分)
。(4分)
(2)由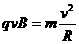 ,求得带电粒子运动半径
,求得带电粒子运动半径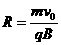 。
。
粒子撞击MN时速度方向与MN板平面的夹角为450的可能性有图甲、图乙两种可能。
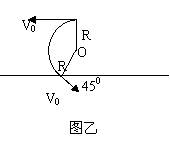 设MN间距为d,由图甲,有.R-Rcos450=0.5d
设MN间距为d,由图甲,有.R-Rcos450=0.5d
解得.d=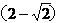
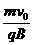 对应时间为.t=
对应时间为.t=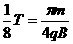 (3分)
(3分)
由图乙.有.R+Rcos450=0.5d
解得.d=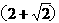
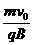 对应时间为.t=
对应时间为.t=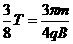 (3分)
(3分)
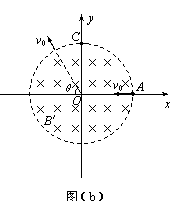
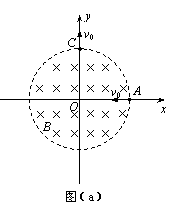
30.湖南省长沙市一中·雅礼中学2010届高三三月联考如图(a)所示,在以直角坐标系xOy的坐标原点O为圆心、半径为r的圆形区域内,存在磁感应强度大小为B、方向垂直xOy所在平面的匀强磁场。一带电粒子由磁场边界与x轴的交点A处,以速度v0沿x轴负方向射入磁场,粒子恰好能从磁场边界与y轴的交点C处,沿y轴正方向飞出磁场,不计带电粒子所受重力。
 (1)求粒子的荷质比
(1)求粒子的荷质比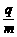 。
。
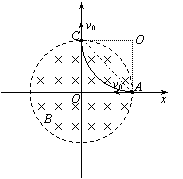
(2)若磁场的方向和所在空间的范围不变,而磁感应强度的大小变为B′,该粒子仍从A处以相同的速度射入磁场,粒子飞出磁场时速度的方向相对于入射方向改变了θ角,如图(b)所示,求磁感应强度B′的大小。
 解析:(1)由几何关系可知,粒子的运动轨迹如图,其半径R=r,
解析:(1)由几何关系可知,粒子的运动轨迹如图,其半径R=r,
洛伦兹力等于向心力,即
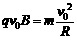 (3分)
(3分)
得 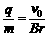 (1分)
(1分)
(2)粒子的运动轨迹如图,设其半径为R′,洛伦兹力提供向心力,即
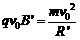 (2分)
(2分)
又因为 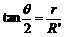 (2分)
(2分)
解得
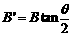 (1分)
(1分)
29.江苏省田家炳实验中学2010届高三上学期期末模拟如图所示,水平地面上有一辆固定有竖直光滑绝缘管的小车,管的底部有一质量m=0.2g、电荷量q=8×10-5C的小球,小球的直径比管的内径略小.在管口所在水平面MN的下方存在着垂直纸面向里、磁感应强度B1= 15T的匀强磁场,MN面的上方还存在着竖直向上、场强E=25V/m的匀强电场和垂直纸面向外、磁感应强度B2=5T的匀强磁场.现让小车始终保持v=2m/s的速度匀速向右运动,以带电小球刚经过场的边界PQ为计时的起点,测得小球对管侧壁的弹力FN随高度h变化的关系如图所示.g取10m/s2,不计空气阻力.求:
(1)小球刚进入磁场B1时的加速度大小a; (2)绝缘管的长度L;
(3)小球离开管后再次经过水平面MN时距管口的距离△x.


解析:(1)以小球为研究对象,竖直方向小球受重力和恒定的洛伦兹力f1,故小球在管中竖直方向做匀加速直线运动,加速度设为a,则
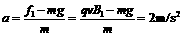
(2)在小球运动到管口时,FN=2.4×10-3N,设v1为小球竖直分速度,由
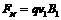 ,则
,则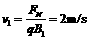
由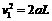 得
得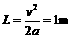
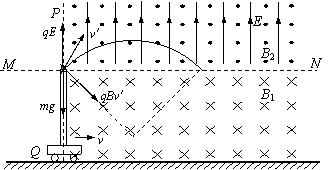
(3)小球离开管口进入复合场,其中qE=2×10-3N,mg=2×10-3N.
 故电场力与重力平衡,小球在复合场中做匀速圆周运动,合速度
故电场力与重力平衡,小球在复合场中做匀速圆周运动,合速度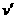 与MN成45°角,轨道半径为R,
与MN成45°角,轨道半径为R,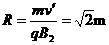
小球离开管口开始计时,到再次经过
MN所通过的水平距离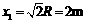
对应时间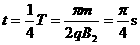
小车运动距离为x2,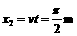
28. 江苏省黄桥中学2010届高三物理校本练习如图所示,真空有一个半径r=0.5m的圆形磁场,与坐标原点相切,磁场的磁感应强度大小B=2×10-3T,方向垂直于纸面向里,在x=r处的虚线右侧有一个方向竖直向上的宽度为L1=0.5m的匀强电场区域,电场强度E=1.5×103N/C.在x=2m处有一垂直x方向的足够长的荧光屏,从O点处向不同方向发射出速率相同的荷质比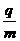 =1×109C/kg带正电的粒子,粒子的运动轨迹在纸面内,一个速度方向沿y轴正方向射入磁场的粒子,恰能从磁场与电场的相切处进入电场。不计重力及阻力的作用。求:
=1×109C/kg带正电的粒子,粒子的运动轨迹在纸面内,一个速度方向沿y轴正方向射入磁场的粒子,恰能从磁场与电场的相切处进入电场。不计重力及阻力的作用。求:
 (1)粒子进入电场时的速度和粒子在磁场中的运动的时间?
(1)粒子进入电场时的速度和粒子在磁场中的运动的时间?
(2)速度方向与y轴正方向成30°(如图中所示)射入磁场的粒子,最后打到荧光屏上,该发光点的位置坐标。
解析:(1)由题意可知:粒子在磁场中做匀速圆周运动的轨道半径R=r=0.5m,
有Bqv=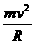 ,可得粒子进入电场时的速度v=
,可得粒子进入电场时的速度v=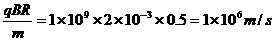
在磁场中运动的时间t1=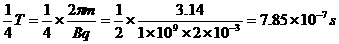
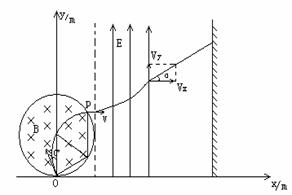 (2)粒子在磁场中转过120°角后从P点垂直电场线进入电场,如图所示,
(2)粒子在磁场中转过120°角后从P点垂直电场线进入电场,如图所示,
在电场中的加速度大小a=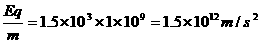
粒子穿出电场时vy=at2=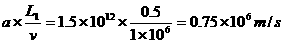 )
)
tanα=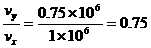
在磁场中y1=1.5r=1.5×0.5=0.75m
在电场中侧移y2=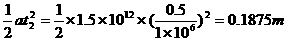
飞出电场后粒子做匀速直线运动y3=L2tanα=(2-0.5-0.5)×0.75=0.75m
故y=y1+y2+y3=0.75m+0.1875m+0.75m=1.6875m 则该发光点的坐标(2 ,1.6875)
27. 广东省廉江三中2010届高三湛江一模预测题如下图所示,在xoy直角坐标系中,第Ⅰ象限内分布着方向垂直纸面向里的匀强磁场,第Ⅱ象限内分布着方向沿y轴负方向的匀强电场。初速度为零、带电量为q、质量为m的离子经过电压为U的电场加速后,从x上的A点垂直x轴进入磁场区域,经磁场偏转后过y轴上的P点且垂直y轴进入电场区域,在电场偏转并击中x轴上的C点。已知OA=OC=d。求电场强度E和磁感强度B的大小.
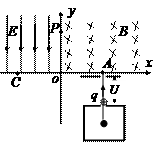 解:设带电粒子经电压为U的电场加速后获得速度为v,由
解:设带电粒子经电压为U的电场加速后获得速度为v,由
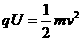 ……①
……①
带电粒子进入磁场后,洛仑兹力提供向心力,由牛顿第二定律:
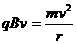 ……②
……②
依题意可知:r=d……③
联立①②③可解得: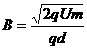 ……④
……④
带电粒子在电场中偏转,做类平抛运动,设经时间t从P点到达C点,由
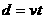 ……⑤
……⑤
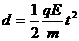 ……⑥
……⑥
联立①⑤⑥可解得: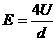 ⑦
⑦
26. 江苏省黄桥中学2010届高三物理校本练习 1932年,劳伦斯和利文斯设计出了回旋加速器。回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计。磁感应强度为B的匀强磁场与盒面垂直。A处粒子源产生的粒子,质量为m、电荷量为+q ,在加速器中被加速,加速电压为U。加速过程中不考虑相对论效应和重力作用。
江苏省黄桥中学2010届高三物理校本练习 1932年,劳伦斯和利文斯设计出了回旋加速器。回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计。磁感应强度为B的匀强磁场与盒面垂直。A处粒子源产生的粒子,质量为m、电荷量为+q ,在加速器中被加速,加速电压为U。加速过程中不考虑相对论效应和重力作用。
(1)求粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比;
(2)求粒子从静止开始加速到出口处所需的时间t ;
(3)实际使用中,磁感应 强度和加速电场频率都有最大值的限制。若某一加速器磁感应强度和加速电场频率的最大值分别为Bm、fm,试讨论粒子能获得的最大动能E㎞。
强度和加速电场频率都有最大值的限制。若某一加速器磁感应强度和加速电场频率的最大值分别为Bm、fm,试讨论粒子能获得的最大动能E㎞。
解析: (1)设粒子第1次经过狭缝后的半径为r1,速度为v1
qu=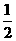 mv12 qv1B=m
mv12 qv1B=m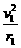 解得
解得 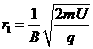
同理,粒子第2次经过狭缝后的半径 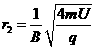 则
则 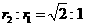
(2)设粒子到出口处被加速了n圈
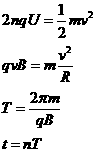 解得
解得 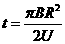
(3)加速电场的频率应等于粒子在磁场中做圆周运动的频率,即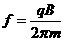
当磁场感应强度为Bm时,加速电场的频率应为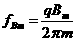
粒子的动能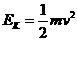
当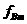 ≤
≤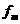 时,粒子的最大动能由Bm决定
时,粒子的最大动能由Bm决定 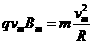 解得
解得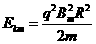
当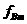 ≥
≥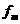 时,粒子的最大动能由fm决定
时,粒子的最大动能由fm决定 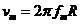 解得
解得 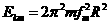
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com