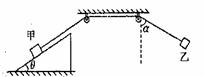
20．在图示的装置中，表面粗糙的斜面固定在地面上，斜面的倾角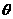=30°．两个光滑的定滑轮的半径很小，用一根跨过定滑轮的细线连接甲、乙两物体，把甲物体放在斜面上且连线与斜面平行，把乙物体拉开使悬线拉直且偏离竖直方向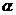=60°．现同时由静止释放甲、乙两物体，乙物体将在竖商平面内摆动，当乙物体运动经过最高点和最低点时，甲物体在斜面上所受摩擦力均为最大但未滑动．已知乙物体的质量m=1kg，取g=10m／s²，下列判断正确的是 ：

　A．乙物体经过最高点时悬线的拉力为5N　　　 B．乙物体经过最低点时悬线的拉力为10N

　C．斜面对甲物体的最大静摩擦力为15N　　　 D．甲物体的质量为2．5kg　　

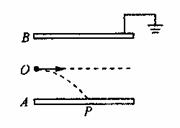
19．如图所示，在真空中有一水平放置的不带电平行板电容器，

板间距离为d，电容为C。上板B接地．现有大量质量均为m、

带电量均为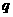的小油滴，以相同的初速度持续不断地从两板正中

央平行极板射入，第一滴油滴正好落到下板A上正中央的P点．

如果能落到A板的油滴仅有N滴，且第N+l滴油滴刚好能飞离电

场，假定落到A板的油滴的电量能被极板全部吸收，不考虑油滴

间的相互作用，将两极板间电场视为匀强电场，重力加速度为g，则不正确的是：

　A．落到A板的油滴数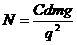 　　 　　　　　B．落到A板油滴数

　C．第N+1滴油滴通过电场的过程中增加的动能为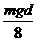

　D．第N+1滴油滴通过电场的过程中减少的机械能为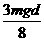

18．设某载人宇宙飞船在距地面高度为4200km的赤道上空绕地球做匀速圆周运动，已知地球半径为6400km，地球同步卫星距地面高为36000km,宇宙飞船和地球同步卫星绕地球同向运动，每当二者相距最近时，宇宙飞船向同步卫星发射信号，然后由同步卫星将信号发送到地面接收站．某时刻二者相距最远，从此时开始在一昼夜内，接收站共收到信号的次数为

　 A．4次　　 　B．6次　　 　C．7次　　 D．8次

17．如图，M是一小型理想变压器，其接线柱a、b接在u=311sin314t V正弦交流电源上，变压器右侧为火灾报警系统电路原理图，其中R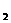为热敏材料制成的传感器，其电阻随温度的升高而减小，电流表A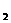为值班室显示器，电压表V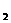显示报警器上的电压(报警器未画出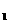)，R、R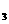，为定值电阻．当传感器R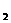所在位置出现火警时,下列判断正确的是：

　A．A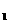示数不变，A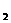示数变大　　　　　 B．A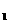示数变大，A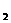示数变大

　C．V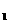示数变大，V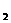示数变大　　　　　 D．V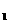示数不变，V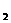示数变小

16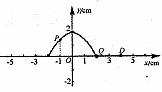．在均匀介质中位于平衡位置的振源质点O，t=0时沿y轴正方向开始做简谐运动，图为t=1s时的波形，当t=2s时振源第一次回到原点且立即停止振动.则：

　A．平衡位置x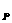=-1m处的质点P与平衡位x 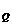=2m处的质点Q在前3s内通过的路程均为4cm

　B．从t=1s至t=1．5s内质点P的速度不断变小

　C．平衡位置x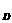 =4m处的质点D，在t=5s时加速度最大

　D．质点P回到平衡位置时，质点D位置坐标为(4m，lcm)

15．图甲所示，在倾角为30°足够长的光滑斜面上，质量为m的物块受到平行于斜面的力F作用，其变化规律如图乙，纵坐标为F与mg的比值，规定力沿斜面向上为正方向，则丙中正确表达物块速度v随时间t变化规律的是(物块初速度为零，g取10m/s)：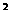

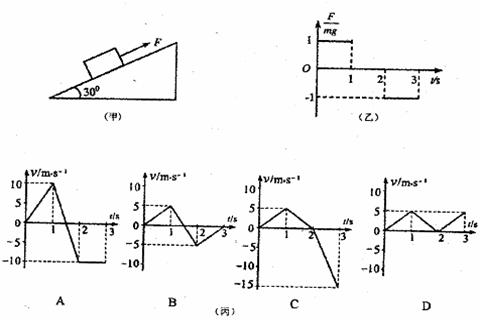
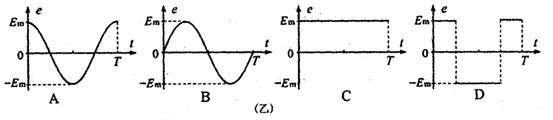
14．甲图为发电机结构示意图，其中N、S是永久磁铁的两个磁极，其表面呈半圆柱面状．M是圆柱形铁芯，它与磁极柱面共轴，铁芯上绕有矩形线框，可绕与铁芯共轴的固定轴转动．磁极与铁芯间的磁场均匀辐向分布．从图示位置开始计时，当线框匀速转动时，乙图中可正确反映线框感应电动势e随时间t变化规律的是：

3．(2008年高考广东卷)一个25 kg的小孩从高度为3.0 m的滑梯顶端由静止开始滑下，滑到底端时的速度为2.0 m/s.取g＝10 m/s²，关于力对小孩做的功，以下结果正确的是(　)

A．合外力做功50 J　 B．阻力做功500 J

C．重力做功500 J　 D．支持力做功50 J

解析：选A.由动能定理可求得合外力做的功等于物体动能的变化ΔE_k＝mv²＝×25×2.0² J＝50 J，A选项正确．重力做功W_G＝mgh＝25×10×3.0 J＝750 J，C选项错误．支持力的方向与小孩的运动方向垂直，不做功，D选项错误．阻力做功W_阻＝W_合－W_G＝(50－750) J＝－700 J，B选项错误．

图5－2－11

4．如图5－2－11所示，质量为m的小车在水平恒力F推动下，从山坡(粗糙)底部A处由静止起运动至高为h的坡顶B，获得速度为v，AB之间的水平距离为s，重力加速度为g.下列说法正确的是(　)

A．小车克服重力所做的功是mgh

B．合外力对小车做的功是mv²

C．推力对小车做的功是mv²+mgh

D．阻力对小车做的功是mv²+mgh－Fs

解析：选ABD.小车克服重力做功W＝Gh＝mgh，A选项正确；由动能定理，小车受到的合力做的功等于小车动能的增加，W_合＝ΔE_k＝mv²，B选项正确；

由动能定理，W_合＝W_推+W_重+W_阻＝mv²，

所以推力做的功W_推＝mv²－W_阻－W_重＝mv²+mgh－W_阻，C选项错误；阻力对小车做的功W_阻＝mv²－W_推－W_重＝mv²+mgh－Fs，D选项正确．

图5－2－12

5．如图5－2－12所示，质量为m的物块与转台之间能出现的最大静摩擦力为物块重力的k倍，物块与转轴OO′相距R，物块随转台由静止开始转动，当转速增加到一定值时，物块即将在转台上滑动，在物块由静止到滑动前的这一过程中，转台的摩擦力对物块做的功为(　)

A．0 　　　　　　　B．2πkmgR

C．2kmgR　 　　　　　D.kmgR

解析：选D.在转速增加的过程中，转台对物块的摩擦力是不断变化的，当转速增加到一定值时，物块在转台上即将滑动，说明此时最大静摩擦力提供向心力，即

kmg＝①

在这一过程中对物块用动能定理

W＝mv²②

由①②知，转台对物块所做的功

W＝kmgR，D对．

图5－2－13

6．如图5－2－13所示，斜面AB和水平面BC是从同一板材上截下的两段，在B处用小圆弧连接．将小铁块(可视为质点)从A处由静止释放后，它沿斜面向下滑行，进入平面，最终静止于P处．若从该板材上再截下一段，搁置在A、P之间，构成一个新的斜面，再将铁块放回A处，并轻推一下使之沿新斜面向下滑动．关于此情况下铁块运动情况的描述，正确的是(　)

A．铁块一定能够到达P点

B．铁块的初速度必须足够大才能到达P点

C．铁块能否到达P点与铁块质量有关

D．以上说法均不对

解析：选A.设AB＝s₁，BP＝s₂，AP＝s₃，动摩擦因数为μ，由动能定理得：mgs₁sinα－μmgcosαs₁－μmgs₂＝0，可得：

mgs₁sinα＝μmg(s₁cosα+s₂)，设沿AP滑到P的速度为v_P，由动能定理得：mgs₁sinα－μmgcosβ·s₃＝mv_P²，因s₁cosα+s₂＝s₃cosβ，故得：v_P＝0，即铁块恰好沿AP滑到P点，故A正确．

图5－2－14

7．如图5－2－14所示，质量相同的物体分别自斜面AC和BC的顶端由静止开始下滑，物体与斜面间的动摩擦因数都相同，物体滑到斜面底部C点时的动能分别为E_k1和E_k2，下滑过程中克服摩擦力所做的功分别为W₁和W₂，则(　)

A．E_k1>E_k2　W₁<W₂　 B．E_k1>E_k2　W₁＝W₂

C．E_k1＝E_k2　W₁>W₂　 D．E_k1<E_k2　W₁>W₂

解析：选B.设斜面的倾角为θ，则下滑过程中克服摩擦力做的功为W＝μmgscosθ＝μmgs_水平，所以两种情况下克服摩擦力做的功相等，再由于B的高度比A低所以E_k1>E_k2，选B.

图5－2－15

8．(2009年高考海南卷)一物体在外力的作用下从静止开始做直线运动，合外力方向不变，大小随时间的变化如图5－2－15所示．设该物体在t₀和2t₀时刻相对于出发点的位移分别是s₁和s₂，速度分别是v₁和v₂，合外力从开始至t₀时刻做的功是W₁，从t₀至2t₀时刻做的功是W₂，则(　)

A．s₂＝5s₁　v₂＝3v₁　 　　　　B．s₂＝9s₁　v₂＝5v₁

C．s₂＝5s₁　W₂＝8W₁ 　　　　D．v₂＝3v₁　W₂＝9W₁

解析：选AC.设t₀时刻前后的加速度分别为a₁、a₂，则a₂＝2a₁，所以v₁＝a₁t₀，v₂＝v₁+a₂t₀＝3v₁；s₁＝a₁t₀²，s₂＝s₁+v₁t₀+a₂t₀²＝5s₁；W₁＝F₀s₁，W₂＝2F₀(s₂－s₁)＝8W₁，故选项A、C对，B、D错．

图5－2－16

9．某物体沿直线运动的v－t关系如图5－2－16所示，已知在第1 s内合外力对物体做的功为W，则(　)

A．从第1 s末到第3 s末合外力做功为4W

B．从第3 s末到第5 s末合外力做功为－2W

C．从第5 s末到第7 s末合外力做功为W

D．从第3 s末到第4 s末合外力做功为－0.75W

解析：选CD.由题图知：第1 s末、第3 s末、第7 s末速度大小关系：v₁＝v₃＝v₇，由题知W＝mv₁²－0，则由动能定理得第1 s末到第3 s末合外力做功W₁＝mv₃²－mv₁²＝0，故A错．第3 s末到第5 s末合外力做功W₂＝mv₅²－mv₃²＝0－mv₁²＝－W，故B错．第5 s末到第7 s末合外力做功W₃＝mv₇²－0＝mv₁²＝W，故C正确．第3 s末到第4 s末合外力做功W₄＝mv₄²－mv₃²＝m(v₁)²－mv₁²＝－0.75W，故D对．

图5－2－17

10．如图5－2－17所示，由细管变成的竖直轨道，其圆形部分的半径为R和r，质量为m的小球从水平轨道出发，先后经过两圆形轨道最后又进入水平轨道，已知小球在A处刚好对管壁无压力，在B处对管的内侧壁压力为0.5mg，试求小球由A至B的运动过程中克服轨道阻力所做的功(细管的内径及球的大小不计)．

解析：设小球在A、B处的速度为v_A、v_B，由题意可知，小球在A处时重力充当小球做圆周运动的向心力，即

mg＝m

在B处，重力与管内侧壁对其的支持力的合力充当向心力，即mg－0.5mg＝m小球由A到B过程运用动能定理得：

mg(2R－2r)－W_f＝mv_B²－mv_A²

联立解得W_f＝mgR－mgr.

答案：mgR－mgr

图5－2－18

11．如图5－2－18所示，质量为M＝0.2 kg的木块放在水平台面上，台面比水平地面高出h＝0.20 m，木块离台的右端L＝1.7 m．质量为m＝0.10M的子弹以v₀＝180 m/s的速度水平射向木块，当子弹以v＝90 m/s的速度水平射出时，木块的速度为v₁＝9 m/s(此过程作用时间极短，可认为木块的位移为零)．若木块落到水平地面时的落地点到台面右端的水平距离为s＝1.6 m，求：

(1)木块对子弹所做的功W₁和子弹对木块所做的功W₂；

(2)木块与台面间的动摩擦因数μ.

解析：(1)由动能定理得，木块对子弹所做的功为

W₁＝mv²－mv₀²＝－243 J.

同理，子弹对木块所做的功为W₂＝Mv₁²＝8.1 J.

(2)设木块离开台面时的速度为v₂，木块在台面上滑行阶段对木块由动能定理，有：－μMgL＝Mv₂²－Mv₁²

木块离开台面后的平抛阶段，s＝v₂.

由以上两式代入数据解得μ＝0.50.

答案：(1)－243 J　8.1 J　(2)0.50

图5－2－19

12．如图5－2－19所示，竖直固定放置的斜面DE与一光滑的圆弧轨道ABC相连，C为切点，圆弧轨道的半径为R，斜面的倾角为θ.现有一质量为m的滑块从D点无初速下滑，滑块可在斜面和圆弧轨道之间做往复运动，已知圆弧轨道的圆心O与A、D在同一水平面上，滑块与斜面间的动摩擦因数为μ，求：

(1)滑块第一次至左侧AC弧上时距A点的最小高度差h.

(2)滑块在斜面上能通过的最大路程s.

解析：(1)由动能定理得：

mgh－μmgcosθ·R/tanθ＝0

得h＝μRcos²θ/sinθ＝μRcosθcotθ.

(2)滑块最终至C点的速度为0时对应在斜面上的总路程最大，由动能定理得mgRcosθ－μmgcosθ·s＝0

得：s＝.

答案：(1)μRcosθcotθ　(2)

6．(2009年大连模拟)如图5－3－17所示，在高1.5 m的光滑平台上有一个质量为2 kg的小球被一细线拴在墙上，球与墙之间有一根被压缩的轻质弹簧．当烧断细线时，小球被弹出，小球落地时的速度方向与水平方向成60°角，则弹簧被压缩时具有的弹性势能为(g取10 m/s²)(　)

图5－3－17

A．10 J　　　　　B．15 J

C．20 J　 　　　　　　　　　D．25 J

解析：选A.由h＝gt²和v_y＝gt得：v_y＝ m/s，

落地时，由tan60°＝可得：v₀＝＝ m/s，

由机械能守恒得：E_p＝mv₀²，可求得：E_p＝10 J，故A正确．

图5－3－18

7．(2008年高考全国卷Ⅱ)如图5－3－18所示，一很长的、不可伸长的柔软轻绳跨过光滑定滑轮，绳两端各系一小球a和b.a球质量为m，静置于地面；b球质量为3m，用手托住，高度为h，此时轻绳刚好拉紧．从静止开始释放b后，a可能达到的最大高度为(　)

A．h　 　　　　　　　　　B．1.5h

C．2h 　　　　　　　　　D．2.5h

解析：选B.绳不可伸长，从静止开始释放b球到b球落地的过程，两球具有共同大小的加速度和共同的速率，有：3mg－mg＝4ma，解得a＝g，则b球落地时a球的速度v＝＝，此后a球以加速度g向上做匀减速直线运动，上升高度h′＝＝0.5h，所以从静止开始释放b球后，a球到达的最大高度为1.5h，故选项B正确．

图5－3－19

8．(2010年福建福州第一次模拟)如图5－3－19所示，小车上有固定支架，一可视为质点的小球用轻质细绳拴挂在支架上的O点处，且可绕O点在竖直平面内做圆周运动，绳长为L.现使小车与小球一起以速度v₀沿水平方向向左匀速运动，当小车突然碰到矮墙后，车立即停止运动，此后小球上升的最大高度可能是(　)

A．大于　 　　　　　　　　B．小于

C．等于　 　　　　　　　　D．等于2L

答案：BCD

图5－3－20

9．有一竖直放置的“T”形架，表面光滑，滑块A、B分别套在水平杆与竖直杆上，A、B用一不可伸长的轻细绳相连，A、B质量相等，且可看作质点，如图5－3－20所示，开始时细绳水平伸直，A、B静止．由静止释放B后，已知当细绳与竖直方向的夹角为60°时，滑块B沿着竖直杆下滑的速度为v，则连接A、B的绳长为(　)

A. 　　　　　　　　　　　　B.

C.　 　　　　　　　　　　　D.

解析：选D.设滑块A的速度为v_A，因绳不可伸长，两滑块沿绳方向的分速度大小相等，得：v_Acos30°＝v_Bcos60°，又v_B＝v，设绳长为s，由A、B组成的系统机械能守恒得：mgscos60°＝mv_A²+mv²，以上两式联立可得：s＝，故选D.

图5－3－21

10．(2010年湖北联考)过山车质量均匀分布，从高为h的平台上无动力冲下倾斜轨道并进入水平轨道，然后进入竖直圆形轨道，如图5－3－21所示，已知过山车的质量为M，长为L，每节车厢长为a，竖直圆形轨道半径为R，L＞2πR，且R≫a，可以认为在圆形轨道最高点的车厢受到前后车厢的拉力沿水平方向，为了不出现脱轨的危险，h至少为多少？(用R、L表示，认为运动时各节车厢速度大小相等，且忽略一切摩擦力及空气阻力)

解析：不出现脱轨的最小速度为车厢恰能通过圆轨道最高点的速度，由mg＝mv²/R得：v＝①

由机械能守恒得：Mgh＝Mv²+·gR②

解①②得：h＝+.

答案：+

图5－3－22

11．如图5－3－22所示，半径为R的圆弧支架竖直放置，圆弧边缘C处有一小滑轮，一轻绳两端系着质量分别为m₁与m₂的物体，挂在定滑轮两边，且m₁＝4m₂，开始时m₁、m₂均静止，且能视为质点，不计一切摩擦，试求m₁到达圆弧的A点时的速度大小．

解析：设m₁运动到圆弧的最低点时，速度为v₁，此时物体m₂的速度为v₂，速度分解如图，得v₂＝v₁cos45°.对m₁、m₂组成的系统，机械能守恒得m₁gR－m₂g·R＝m₁v₁²+m₂v₂²又m₁＝4m₂

由以上三式可求得：v₁＝ .

1．下列物体运动过程中满足机械能守恒的是(　)

A．跳伞运动员张开伞后，在空中匀速下降

B．忽略空气阻力，物体竖直上抛

C．火箭升空

D．拉着物体沿光滑斜面匀速上升

解析：选B.跳伞运动员匀速下降，除重力做功外，还有阻力做功，A错；物体竖直上抛时，只有重力做功，机械能守恒，B正确；火箭升空时，推力做正功，机械能增加，C不正确；拉着物体沿光滑斜面匀速上升时，机械能增加，D不正确．

图5－3－13

2．如图5－3－13所示，一轻质弹簧竖立于地面上，质量为m的小球，自弹簧正上方h高处由静止释放，则从小球接触弹簧到将弹簧压缩至最短(弹簧的形变始终在弹性限度内)的过程中，下列说法正确的是(　)

A．小球的机械能守恒

B．重力对小球做正功，小球的重力势能减小

C．由于弹簧的弹力对小球做负功，所以弹簧的弹性势能一直减小

D．小球的加速度一直减小

解析：选B.小球与弹簧作用过程，弹簧弹力对小球做负功，小球的机械能减小，转化为弹簧的弹性势能，使弹性势能增加，因此A错误，C错误；小球下落过程中重力对小球做正功，小球的重力势能减小，B正确；分析小球受力情况，由牛顿第二定律得：mg－kx＝ma，随弹簧压缩量的增大，小球的加速度a先减小后增大，故D错误．

图5－3－14

3．(2010年江苏启东中学质检)如图5－3－14所示，A、B两球质量相等，A球用不能伸长的轻绳系于O点，B球用轻弹簧系于O′点，O与O′点在同一水平面上，分别将A、B球拉到与悬点等高处，使绳和轻弹簧均处于水平，弹簧处于自然状态，将两球分别由静止开始释放，当两球达到各自悬点的正下方时，两球仍处在同一水平面上，则(　)

A．两球到达各自悬点的正下方时，两球动能相等

B．两球到达各自悬点的正下方时，A球动能较大

C．两球到达各自悬点的正下方时，B球动能较大

D．两球到达各自悬点的正下方时，A球受到向上的拉力较大

解析：选BD.整个过程中两球减少的重力势能相等，A球减少的重力势能完全转化为A球的动能，B球减少的重力势能转化为B球的动能和弹簧的弹性势能，所以A球的动能大于B球的动能，所以B正确；在O点正下方位置根据牛顿第二定律，小球所受拉力与重力的合力提供向心力，则A球受到的拉力较大，所以D正确．

图5－3－15

4．如图5－3－15所示，在两个质量分别为m和2m的小球a和b之间，用一根长为L的轻杆连接(杆的质量可不计)，而小球可绕穿过轻杆中心O的水平轴无摩擦转动，现让轻杆处于水平位置，然后无初速度释放，重球b向下，轻球a向上，产生转动，在杆转至竖直的过程中(　)

A．b球的重力势能减小，动能增加

B．a球的重力势能增加，动能减小

C．a球和b球的总机械能守恒

D．a球和b球的总机械能不守恒

解析：选AC.两球组成的系统，在运动中除动能和势能外没有其他形式的能转化，所以系统的机械能守恒．

图5－3－16

5．(2010年江苏启东中学质检)如图5－3－16所示，质量相等的甲、乙两物体开始时分别位于同一水平线上的A、B两点．当甲物体被水平抛出的同时，乙物体开始自由下落．曲线AC为甲物体的运动轨迹，直线BC为乙物体的运动轨迹，两轨迹相交于C点，空气阻力忽略不计．则两物体(　)

A．在C点相遇

B．经C点时速率相等

C．在C点时具有的机械能相等

D．在C点时重力的功率相等

解析：选AD.甲做平抛运动的同时乙做自由落体运动，平抛运动可以看作竖直方向的自由落体运动和水平方向的匀速直线运动，所以竖直方向上甲乙运动的情况相同，交点表示两物体相遇的位置，所以A正确；在C位置，甲竖直方向的速度与乙的速度相等，重力相等所以重力的功率相等，故D正确；而甲具有水平方向的速度，所以甲的速率大于乙的速率，B错误，此时两物体重力势能相等，但是甲的动能大于乙的动能，所以甲的机械能大于乙的机械能，故C错误．