
题目列表(包括答案和解析)
1.首先明确所给的图象是什么图象,即认清图象中横、纵轴所代表的物理量及它们的函数关系.特别是那些图形相似容易混淆的图象,更要注意区分.
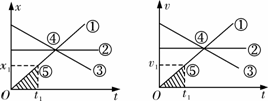
形状相同的图线,在不同的图象中所表示的物理规律不同,通过下图中的例子体会x-t图象和v-t图象中图线表示的物理规律.
|
x-t图象 |
v-t图象 |
|
①表示物体做匀速直线运动(斜率表示速度v); ②表示物体静止; ③表示物体向负方向做匀速直线运动; ④交点的纵坐标表示三个运动质点相遇时的位移; ⑤t1时刻物体位移为x1(图中阴影部分的面积没有意义) |
①表示物体做匀加速直线运动(斜率表示加速度a); ②表示物体做匀速直线运动; ③表示物体做匀减速直线运动; ④交点的纵坐标表示三个运动质点的共同速度; ⑤t1时刻物体速度为v1(图中阴影部分面积表示质点①在0-t1时间内的位移) |
2.速度—时间图象(v-t图象)
(1)物理意义:反映了做直线运动的物体的 速度 随 时间 的变化关系.
(2)图线斜率的意义
①图线上某点切线的斜率大小表示物体运动的 加速度的大小 .
②图线上某点切线的斜率正负表示加速度的 方向 .
(3)两种特殊的v-t图象
①匀速直线运动的v-t图象是与横轴 平行 的直线.
②匀变速直线运动的v-t图象是一条 倾斜 的直线.
(4)图象与时间轴围成的“面积”的意义
①图象与时间轴围成的“面积”表示相应时间内的 位移 .
② 若此面积在时间轴的上方,表示这段时间内的位移方向为 正方向 ;若此面积在时间轴的下方,表示这段时间内的位移方向为 负方向 .
重点难点突破
1.位移—时间图象(x-t图象)
(1)x-t图象的物理意义:反映做直线运动的物体的 位移 随时间变化的关系.
(2)图线斜率的意义
①图线上某点切线的斜率大小表示物体 速度的大小 .
②图线上某点切线的斜率正负表示物体 速度的方向 .
(3)两种特殊的x-t图象
①若x-t图象是一条倾斜的直线,说明物体做 匀速直线 运动.
②若x-t图象是一条平行于时间轴的直线,说明物体处于 静止 状态.
3.运动学规律在行车问题中的应用
[例4]汽车初速度v0=20 m/s,刹车后做匀减速直线运动,加速度大小为a=5 m/s2,求:
(1)开始刹车后6 s末汽车的速度;
(2)10 s末汽车的位置.
[错解](1)由v=v0+at,得6 s末汽车的速度为
vt=20 m/s+[(-5)×6] m/s=-10 m/s
负号表示与运动方向相反.
(2)10 s末汽车的位移为
x=v0t+ at2=[20×10+
at2=[20×10+ ×(-5)×102] m=-50
m
×(-5)×102] m=-50
m
负号表示汽车在开始刹车处后方50 m处.
[错因]没有考虑到汽车刹车后的实际运动情况是速度减为零后,汽车将停下,而不再做反向的匀加速运动.
[正解](1)设汽车经过时间t速度减为零,
则由vt=v0+at,得t=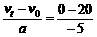 s=4 s
s=4 s
故6 s后汽车速度为零.
(2)由(1)知汽车4 s后就停止,则
x=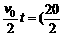 ×4) m=40 m
×4) m=40 m
即汽车10 s末位置在开始刹车点前方40 m处.
[思维提升]竖直上抛运动的物体,速度先减为零,然后反向做匀加速运动.而刹车之类的问题,物体速度减为零后停止运动,不再反向做加速运动,因此对于此类问题首先要弄清停下需经历多少时间或多少位移.
第 3 课时 运动图象的探究分析及应用
基础知识归纳
2.匀变速直线运动的推论及其应用
[例2]物体沿一直线运动,在t时间内通过的位移为x,它在中间位置 x处的速度为v1,在中间时刻
x处的速度为v1,在中间时刻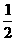 t时的速度为v2,则v1和v2的关系为
( )
t时的速度为v2,则v1和v2的关系为
( )
A.当物体做匀加速直线运动时,v1>v2 B.当物体做匀减速直线运动时,v1>v2
C.当物体做匀速直线运动时,v1=v2 D.当物体做匀减速直线运动时,v1<v2
[解析]本题主要考查对中间时刻速度和中点位置速度的理解及比较.
设物体运动的初速度为v0,末速度为vt,有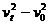 =2a•x
①
=2a•x
①
 ②
②
由①②式解得v1=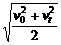 ③
③
由速度公式可求得v2=(v0+vt)/2 ④
而③④两式,对匀加速、匀减速直线运动均成立.用数学方法可知,只要v0≠vt,必有v1>v2;当v0=vt,做匀速直线运动,必有v1=v2.所以,正确选项应为A、B、C.
[答案]ABC
[思维提升]解题时要注意:当推出v1>v2时假设物体做匀加速运动,不能主观地认为若物体做匀减速运动结果就是v1<v2.
[拓展2]一列火车由静止开始做匀加速直线运动,一个人站在第1节车厢前端的站台前观察,第1节车厢通过他历时2 s,全部车厢通过他历时8 s,忽略车厢之间的距离,车厢长度相等,求:
(1)这列火车共有多少节车厢?
(2)第9节车厢通过他所用的时间为多少?
[解析](1)根据做初速度为零的匀加速直线运动的物体,连续通过相等位移所用时间之比为
1∶(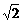 -1)∶(
-1)∶(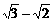 )∶…∶(
)∶…∶(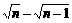 )
)
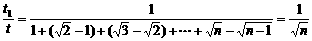
所以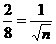 ,n=16,故这列火车共有16节车厢.
,n=16,故这列火车共有16节车厢.
(2)设第9节车厢通过他所用时间为t9,则
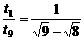 ,t9=
,t9=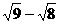 t1=(6-
t1=(6-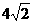 ) s=0.34 s
) s=0.34 s
[例3]将粉笔头A轻放在以2 m/s的恒定速度运动的足够长的水平传送带上后,传送带上留下一条长度为4 m的划线.若使该传送带改做初速度不变、加速度大小为1.5 m/s2的匀减速运动直至速度为零,并且在传送带开始做匀减速运动的同时,将另一粉笔头B轻放在传送带上,则粉笔头B停止在传送带上的位置与划线起点间的距离为多少?(g取10 m/s2)
[解析]粉笔头A在传送带上运动,设其加速度为a,加速时间为t,则vt- at2=4
m,at=2 m/s,所以a=0.5 m/s2
at2=4
m,at=2 m/s,所以a=0.5 m/s2
若传送带做匀减速运动,设粉笔头B的加速度时间为t1,有v1=at1=v-a′t1.所以t1=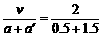 s=1 s
s=1 s
此时粉笔头B在传送带上留下的划线长为l1=x传送带-x粉笔=(vt1-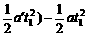 =2×
=2×
1 m- ×1.5×12 m-
×1.5×12 m- ×0.5×12 m=1 m
×0.5×12 m=1 m
因传送带提供给粉笔的加速度大小为0.5 m/s2,小于1.5 m/s2.故粉笔相对传送带向前滑,到传送带速度减为零时,有v1=a′t2,v2=v1-at2,l2=x粉笔-x传送带=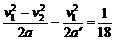 m
m
传送带停止运动后,粉笔继续在传送带上做匀减速运动直至停止.则l3=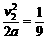 m,所以Δl=l1-l2-l3=
m,所以Δl=l1-l2-l3=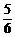 m
m
[思维提升]粉笔头A在第一种情况下先做匀加速运动;粉笔头B在第二种情况下先做匀加速运动,后做匀减速运动.求解时不仅要注意粉笔头各运动阶段的物理量间关系,还要注意其与传送带运动的各物理量间的关系.
 易错门诊
易错门诊
1.匀变速直线运动问题的求解
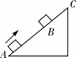 [例1]物体以一定的初速度从A点冲上固定的光滑的斜面,到达斜面最高点C时速度恰好为零,如图所示.已知物体运动到斜面长度3/4处的B点时,所用时间为t,求物体从B运动到C所用的时间.
[例1]物体以一定的初速度从A点冲上固定的光滑的斜面,到达斜面最高点C时速度恰好为零,如图所示.已知物体运动到斜面长度3/4处的B点时,所用时间为t,求物体从B运动到C所用的时间.
[解析]解法一:逆向思维法
物体向上匀减速冲上斜面,相当于向下匀加速滑下斜面.故xBC= ,xAC=a(t+tBC)2/2,又xBC=xAC/4
,xAC=a(t+tBC)2/2,又xBC=xAC/4
解得tBC=t
解法二:比例法
对于初速度为零的匀变速直线运动,在连续相等的时间内通过的位移之比为
x1∶x2∶x3∶…∶xn=1∶3∶5∶…∶(2n-1)
现在xBC∶xAB=1∶3
通过xAB的时间为t,故通过xBC的时间tBC=t
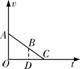 解法三:利用相似三角形面积之比等于对应边平方比的方法,作出v-t图象,如图所示.
解法三:利用相似三角形面积之比等于对应边平方比的方法,作出v-t图象,如图所示.
S△AOC/S△BDC=CO2/CD2
且S△AOC=4S△BDC,OD=t,OC=t+tBC
所以4/1=(t+tBC)2/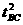 ,解得tBC=t
,解得tBC=t
[思维提升]本题解法很多,通过对该题解法的挖掘,可以提高灵活应用匀变速直线运动规律和推论的能力、逆向思维的能力及灵活运用数学知识处理物理问题的能力.
[拓展1]一个做匀加速直线运动的物体,在头4 s内经过的位移为24 m,在第二个4 s内经过的位移是60 m.求这个物体的加速度和初速度各是多少?
[解析]解法一:基本公式法
头4 s内的位移:x1=v0t+ at2
at2
第2个4 s内的位移:x2=v0(2t)+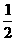 a(2t)2-(v0t+
a(2t)2-(v0t+ at2)
at2)
将x1=24 m、x2=60 m、t=4 s代入上式,
解得a=2.25 m/s2,v0=1.5 m/s
解法二:物体在8 s内的平均速度等于中间时刻(即第4 s 末)的瞬时速度,则v1=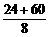 m/s=v0+4a,物体在前4 s内的平均速度等于第2
s末的瞬时速度v2=
m/s=v0+4a,物体在前4 s内的平均速度等于第2
s末的瞬时速度v2=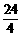 m/s=v0+2a
m/s=v0+2a
两式联立解得a=2.25 m/s2,v0=1.5 m/s
解法三:由公式Δx=aT2,得a=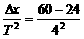 m/s2=2.25 m/s2
m/s2=2.25 m/s2
根据v1=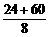 m/s=v0+4a,所以v0=1.5 m/s
m/s=v0+4a,所以v0=1.5 m/s
5.末速度为零的匀减速运动,是加速度大小相同、初速度为零的匀加速运动的逆过程,因此可将其转化为初速度为零的匀加速运动进行计算,使运算简便.
 典例精析
典例精析
4.公式应用过程中,如需解二次方程,则必须对求解的结果进行讨论.
3.在计算飞机着陆、汽车刹车等这类速度减为零后不能反向运动的减速运动的位移时,注意判断所给时间t内物体是否已经停止运动.如果已停止运动,则不能用时间t代入公式求位移,而应求出它停止所需的时间t′,将t′代入公式求位移.因为在以后的t′-t时间内物体已停止运动,位移公式对它已不适用.此种情况称为“时间过量问题”.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com