
题目列表(包括答案和解析)
1.时间的对称性
(1)物体上升到最高点所用时间与物体从最高点落回到原抛出点所用时间相等:t上=t下=v0/g.
(2)物体在上升过程中从某点到达最高点所用的时间和从最高点落回该点所用的时间相等.
自由落体运动是初速度v0=0、加速度为重力加速度g的匀加速直线运动的特例,故匀变速直线运动的基本公式和相关推论式对自由落体运动都适用.
2.竖直上抛运动
(1)竖直上抛运动的特点
①上升阶段:速度越来 越小 ,加速度与速度方向 相反 ,是 匀减速直线 运动.
②下降阶段:速度越来 越大 ,加速度与速度方向 相同 ,是 匀加速直线 运动.
③在最高点:速度为 零 ,但加速度仍为 重力速度g ,所以物体此时并不处于平衡状态.
(2)竖直上抛运动的规律
①速度公式:vt= v0-gt .
②位移公式:h=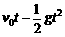 .
.
③速度-位移关系式: = -2gh .
= -2gh .
(3)几个特征量
①上升的最大高度:H=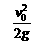 .
.
②上升到最大高度处所需时间t上和最高点处落回原抛出点所需时间t下相等,即t上=t下=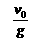 .
.
重点难点突破
1.自由落体运动
(1)自由落体运动的特点
自由落体运动是初速度为 零 ,加速度为 重力加速度g 的匀加速度直线运动.
(2)自由落体运动的运动规律
①速度公式:vt= gt .
②位移公式:h=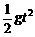 .
.
③速度位移关系式: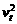 = 2gh .
= 2gh .
④从运动开始连续相等的时间内位移之比为 1∶3∶5∶7∶… .
⑤连续相等的时间t内位移的增加量相等,即Δx= gt2 .
⑥一段时间内的平均速度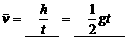 .
.
4.位移图象与运动轨迹的区别
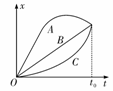 [例4]如图所示,为A、B、C三物体从同一地点、同时出发沿同一方向做直线运动的xt图象,在0-t0时间内( )
[例4]如图所示,为A、B、C三物体从同一地点、同时出发沿同一方向做直线运动的xt图象,在0-t0时间内( )
A.平均速度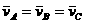 B.平均速率
B.平均速率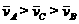
C.A一直在B、C的后面 D.A的速度一直比B、C的速度大
[错解]由x-t图象可知,A、B、C的路程大小关系是sA>sC>sB,故平均速率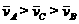 ,所以选B.又从起点O到终点的有向线段长相等,故位移相同,则平均速度相同,A也正确.
,所以选B.又从起点O到终点的有向线段长相等,故位移相同,则平均速度相同,A也正确.
[错因]上述错误的原因是没有明确x-t图象表示位移随时间的变化关系,并非物体的运动的轨迹.
[正解]从x-t图象知,在t0时刻A、B、C离起点O的位移相同,故A正确.由A在时刻t0已经返回到终点,故路程关系是sA>sC=sB,故平均速率vA>vC=vB,B不正确.
[答案]A
[思维提升]对于图象问题,首先要弄清坐标轴表示的意义,然后再弄清图线所描述的规律.本题的图线描述的是位移随时间变化的规律,而不是物体的运动轨迹.
第 4 课时 自由落体运动及抛体运动
基础知识归纳
3.应用图象分析问题
[例3]摩托车在平直公路上从静止开始启动,a1=1.6 m/s2,稍后匀速运动,然后减速,a2=6.4 m/s2,直到停止,共历时130 s,行程1 600 m,试求:
(1)摩托车行驶的最大速度;
(2)若摩托车从静止启动,a1、a2不变,直至停止,行程不变,所需最短时间为多少.
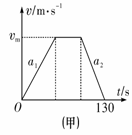 [解析]画出v-t图象如图(甲).
[解析]画出v-t图象如图(甲).
(1)由v2-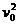 =2ax,有
=2ax,有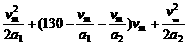 =1 600
=1 600
而a1=1.6 m/s2
a2=6.4 m/s2
解得vm=12.8 m/s(舍去另一解)
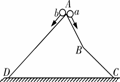
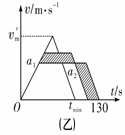 (2)路程不变,则图象中面积不变,当v越大则t越小,如图(乙)所示.设最短时间为tmin,则
(2)路程不变,则图象中面积不变,当v越大则t越小,如图(乙)所示.设最短时间为tmin,则
tmin=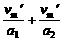 ①
①
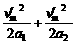 =1 600
②
=1 600
②
其中a1=1.6 m/s2,a2=6.4 m/s2
由②式得vm′=64 m/s
故tmin=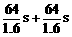 =50 s
=50 s
即最短时间为50 s.
 [思维提升]利用公式和图象,都可以求出最大速度、最短时间等极值问题,但用图象法显然更直观、简洁.
[思维提升]利用公式和图象,都可以求出最大速度、最短时间等极值问题,但用图象法显然更直观、简洁.
[拓展2]如图所示,两个光滑的斜面高度相同,右边由两部分组成且AB+BC=AD,两小球a、b分别从A点沿两侧斜面由静止滑下,不计转折处的能量损失,哪一边的小球先滑到斜面底端.
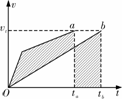 [解析]两小球从等高处沿光滑的斜面下滑(由静止),由于两边斜面倾角不同,下滑的加速度不同(aAB>aAD>aBC),根据机械能守恒定律,两球达到底端的速度大小相等,因此画出其vt图象如图所示,其中折线为沿ABC斜面下滑的a球的速度图象,直线为沿AD斜面下滑的b球的速度图象.
[解析]两小球从等高处沿光滑的斜面下滑(由静止),由于两边斜面倾角不同,下滑的加速度不同(aAB>aAD>aBC),根据机械能守恒定律,两球达到底端的速度大小相等,因此画出其vt图象如图所示,其中折线为沿ABC斜面下滑的a球的速度图象,直线为沿AD斜面下滑的b球的速度图象.
要满足a、b两图线下方的面积相等,必须使图中画有斜线部分的两块面积相等,那就一定有ta<tb,即沿ABC下滑的小球先到达底端.
 易错门诊
易错门诊
2.运动图象的识别和应用
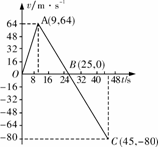 [例2]一宇宙空间探测器从某一星球表面垂直升空,假设探测器的质量恒为1 500 kg,发动机的推力为恒力,宇宙探测器升空到某一高度时,发动机突然关闭,如图所示为其速度随时间变化的规律.
[例2]一宇宙空间探测器从某一星球表面垂直升空,假设探测器的质量恒为1 500 kg,发动机的推力为恒力,宇宙探测器升空到某一高度时,发动机突然关闭,如图所示为其速度随时间变化的规律.
(1)升高后9 s、25 s、45 s,即在图线上A、B、C三点探测器的运动情况如何?
(2)求探测器在该行星表面达到的最大高度
(3)计算该行星表面的重力加速度及发动机的推动力(假设行星表面没有空气).
[解析](1)升空后探测器做初速为零的匀加速直线运动.9 s末发动机关闭,此时速度最大,此后做匀减速运动,25 s末速度减为零,此时探测器离行星表面最高,然后探测器返回做自由落体运动,45 s末落地,速度为80 m/s.
(2)由上述分析可知25 s末探测器距行星表面最高,最大高度hm= ×25×64 m=800 m
×25×64 m=800 m
(3)由9 s-45 s计算图线的斜率可得该行星的重力加速度g=(80+64)/(45-9) m/s2=
4 m/s2.对0-9
s过程运用牛顿第二定律有:F-mg=ma,而a=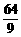 m/s2≈7.1
m/s2
m/s2≈7.1
m/s2
F=m(g+a)=1 500×(4+7.1) N=1.665×104 N
[思维提升]分析速度—时间图象,把握运动状态的变化是解此题的关键.
能用位移—时间图象表示出来的运动应该是直线运动;根据位移是否随时间均匀变化(或图象是否是直线)判断是否是匀速直线运动;根据位移的大小随时间变化的情况判断运动方向是否改变.位移图象和运动轨迹不能混为一谈.
 典例精析
典例精析
1.运动图象的比较
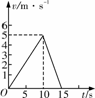 [例1]做直线运动的物体的v-t图象如图所示.由图象可知( )
[例1]做直线运动的物体的v-t图象如图所示.由图象可知( )
A.前10 s物体的加速度为0.5 m/s2,后5 s物体的加速度为-1 m/s2
B.15 s末物体回到出发点
C.10 s末物体的运动方向发生变化
D.10 s末物体的加速度方向发生变化
[解析]从图线的斜率可知物体在前10 s内的加速度为0.5 m/s2,后5 s内的加速度为
-1 m/s2,A正确.物体先沿正方向做匀加速直线运动,10 s末开始做匀减速直线运动,运动方向不变,加速度方向发生了变化,15 s末物体速度为零,离出发点距离37.5 m,选项D正确,B、C错误.
[答案]AD
[思维提升]应用v-t图象分析物体的运动时,要抓住图线的特征与运动性质的关系,要抓住图线的“点”、“线”、“面积”和“斜率”的意义.
[拓展1]若将上题中的图象的纵轴(v轴)换成x轴,其他条件不变,试回答下列问题:
(1)物体在0-10 s和10 s-15 s两个阶段分别做什么运动?
(2)物体何时距出发点最远,何时回到出发点?
[解析](1)0-10 s内,物体的速度为v1=k1=0.5 m/s,物体沿x轴正方向做匀速直线运动.10 s-15 s内,物体的速度为v2=k2=-1 m/s,物体沿x轴负方向做匀速直线运动.
(2)从图可直接判断,物体10 s末离出发点最远,最远距离为5 m;第15 s时,物体位移为0,回到出发点.
图象在中学物理中应用十分广泛,它能形象地表达物理规律,直观地叙述物理过程,并鲜明地表示物理量间的各种关系.利用图象解决物理问题,是学习物理的一种重要方法.
2.要清楚地理解图象中的“点”、“线”、“斜率”、“截距”、“面积”的物理意义:
(1)点:图线上的每一个点对应研究对象的一个状态,特别要注意“起点”、“终点”、“拐点”,它们往往对应一个特殊状态.
(2)线:表示研究对象的变化过程和规律,如v-t图象中图线若为倾斜直线,则表示物体做匀变速直线运动.
(3)斜率:表示横、纵坐标上两物理量的比值,常有一个重要的物理量与之对应,用于求解定量计算对应物理量的大小和定性分析变化的快慢问题.如x-t图象的斜率表示速度的大小,v-t图象的斜率表示加速度的大小.
(4)面积:图线与坐标轴围成的面积常与某一表示过程的物理量相对应.如v-t图象与横轴包围的“面积”大小表示位移大小.
(5)截距:表示横、纵坐标两物理量在“边界”条件下的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com