
题目列表(包括答案和解析)
3.相遇问题的常见情况
(1)同向运动的两物体追及即相遇.
(2)相向运动的物体,当各自发生的位移大小和等于开始时两物体的距离时即相遇.
重点难点突破
2.追及问题的两类情况
(1)速度大者减速(如匀减速直线运动)追速度小者(如匀速运动):
①当两者速度相等时,若两者位移之差仍小于初始时的距离,则永远追不上,此时两者间有 最小 距离.
②若两者位移之差等于初始时的距离,且两者速度相等时,则恰能追上,也是两者相遇时 避免碰撞 的临界条件.
③若两者位移之差等于初始时的距离时,追者速度仍大于被追者的速度,则被追者还有一次追上追者的机会,其间速度相等时两者间距离有 一个极大 值.
(2)速度小者加速(如初速度为零的匀加速直线运动)追速度大者(如匀速运动):
①当两者速度相等时有 最大距离 .
②若两者位移之差等于初始时的距离时,则追上.
1.追及和相遇问题
当两个物体在同一直线上运动时,由于两物体的运动情况不同,所以两物体之间的距离会不断发生变化,两物体间距会越来越大或越来越小,这时就会涉及追及、相遇或避免碰撞等问题.
5.91 s
由v2=2gx得v=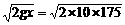 m/s≈59.1
m/s
m/s≈59.1
m/s
即重物从气球上脱落,经5.91 s能落到地面,到达地面时的速度约为59.1 m/s.
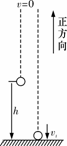 [错因]由于对惯性理解不深刻,导致对题中的隐含条件即重物离开气球时具有向上的初速度视而不见,误认为v0=0.实际上,重物随气球匀速上升时,具有向上10
m/s的速度,当重物离开气球时,由于惯性重物将继续向上运动一段距离,在重力作用下做匀变速直线运动.
[错因]由于对惯性理解不深刻,导致对题中的隐含条件即重物离开气球时具有向上的初速度视而不见,误认为v0=0.实际上,重物随气球匀速上升时,具有向上10
m/s的速度,当重物离开气球时,由于惯性重物将继续向上运动一段距离,在重力作用下做匀变速直线运动.
[正解]取全过程作一整体进行研究,如图所示,则物体在掉落后的时间
t内的位移
h=-175 m
由位移公式h=v0t- gt2得
gt2得
-175=10t-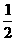 ×10t2
×10t2
解得t=7 s和t=-5 s(舍去)
所以重物落地速度为
vt=v0-gt=-60 m/s
其中负号表示方向向下,与初速度方向相反.
[思维提升](1)研究竖直上抛运动时,要灵活选用分段法和整体法,同时要注意各物理量的取值正负.
(2)画好过程示意图是解决运动学问题的关键.同时正确判断物体的运动情况.
第 5 课时 追及与相遇问题
基础知识归纳
3.竖直上抛运动的处理方法
[例3]气球以10 m/s的速度匀速上升,当它上升到 175 m的高处时,一重物从气球上掉落,则重物需要经过多长时间才能落到地面?到达地面时的速度是多大?(g取10 m/s2)
[错解]因为物体离开气球做自由落体运动,由x= gt2得t=
gt2得t=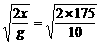 s≈
s≈
2.竖直上抛运动的对称性
[例2]以v0=20 m/s速度竖直上抛一个小球,2 s后以相同的初速度在同一位置上抛另一小球,g=10 m/s2,则两球相碰处离出发点的高度是多少?
[解析]解法一:由速度对称性,上升阶段与下降阶段经过相同的位置时速度等大、反向,即
-[v0-g(t+2)]=v0-gt
解得t=1
s,代入位移公式h=v0t-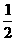 gt2,知h=15 m
gt2,知h=15 m
解法二:根据时间对称,上升和下降经过同一段位移时所用时间相同,即
v0(t+2)-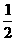 g(t+2)2=v0t-
g(t+2)2=v0t-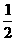 gt2
gt2
解得t=1
s,代入位移公式h=v0t- gt2,知h=15 m
gt2,知h=15 m
[思维提升]运用竖直上抛运动的对称性分析解决物理问题,不仅可以加深对竖直上抛运动的理解和认识,还可以活跃思维,提升能力.
[拓展2]一个从地面竖直上抛的物体,两次经过一个较低点a的时间间隔是Ta,两次经过一个较高点b的时间间隔是Tb,则a、b之间的距离为 ( A )
A.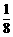 g(
g(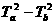 ) B.
) B. g(
g(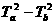 ) C.
) C. g(
g(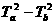 ) D.
) D.  g(Ta-Tb)
g(Ta-Tb)
[解析]根据时间的对称性,物体从a点到最高点的时间为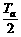 ,从b点到最高点的时间为
,从b点到最高点的时间为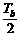 .所以a点到最高点的距离ha=
.所以a点到最高点的距离ha=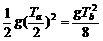
b点到最高点的距离hb=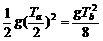
故a、b之间的距离为ha-hb=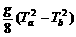 ,即选A.
,即选A.
 易错门诊
易错门诊
1.自由落体运动的规律及其应用
[例1]一个物体从H高处自由落下,经过最后196 m所用的时间是4 s,求物体下落H高所用的总时间T和高度H是多少?(取g=9.8 m/s2,空气阻力不计)
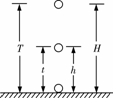 [解析]根据题意画出小球的运动示意图(如图所示)其中t=4 s,h=196 m
[解析]根据题意画出小球的运动示意图(如图所示)其中t=4 s,h=196 m
解法一:根据自由落体公式
由H= gT 2
gT 2
H-h= g(T-t)2解得
g(T-t)2解得
T=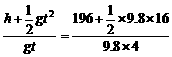 s=7 s
s=7 s
H= gT 2=
gT 2= ×9.8×72
m=240.1 m
×9.8×72
m=240.1 m
解法二:利用匀变速直线运动的平均速度的性质解题.
由题意得最后4 s内的平均速度为
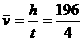 m/s=49 m/s
m/s=49 m/s
因为在匀变速直线运动中,某段时间的平均速度等于中间时刻的速度,所以下落至最后2 s时的瞬时速度为
vt′=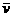 =49 m/s
=49 m/s
由速度公式得从开始下落至最后2 s的时间
t′=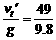 s=5 s
s=5 s
所以T=t′+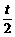 =5 s+
=5 s+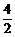 s=7 s
s=7 s
H= gT 2=
gT 2= ×9.8×72
m=240.1 m
×9.8×72
m=240.1 m
[思维提升]解决自由落体运动问题要弄清运动过程,作好示意图,然后利用自由落体运动规律分析求解;同时要注意自由落体运动是初速度v0=0的匀加速直线运动,可灵活运用相关推论求解.
[拓展1]屋檐定时滴出水滴,当第5滴正欲滴下时,第1滴已刚好达到地面,而第3滴与第2滴正分别位于高1 m的窗户上、下沿,如图所示,取g=10 m/s2,问: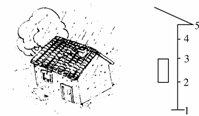
(1)此屋檐离地面多少米?
(2)滴水的时间间隔是多少?
[解析](1)初速度为零的匀加速直线运动从开始运动起,连续相等时间内位移比为1∶3∶5∶…∶(2n-1),令相邻两水滴间的距离从上到下的比依次为x∶3x∶5x∶7x.
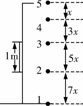 由题意知,窗高为5x,则
由题意知,窗高为5x,则
5x=1 m,x=0.2 m
屋檐高h=x+3x+5x+7x=3.2 m
(2)由公式h=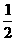 gt2得一滴水落地的时间为t=
gt2得一滴水落地的时间为t=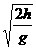 =0.8 s,T=
=0.8 s,T=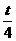 =0.2 s
=0.2 s
2.整体法
(1)将上升和下降过程统一看成是初速度v0向上,加速度g向下的匀变速直线运动,vt=v0-gt,h=v0t- gt2.
gt2.
(2)若vt>0,则物体在上升;vt<0,则物体在下落.h>0,物体在抛出点上方;h<0,物体在抛出点下方.
 典例精析
典例精析
1.分段法
(1)上升过程:vt=0,a=-g的匀减速直线运动.
(2)下降过程:自由落体运动.
2.速度的对称性
(1)物体上抛时的初速度与物体又落回原抛出点时的速度大小相等、方向相反.
(2)在竖直上抛运动中,同一个位置对应两个等大反向的速度.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com