
题目列表(包括答案和解析)
2.临界、极值问题的求解方法
(1)极限法:在题目中如出现“最大”、“最小”、“刚好”等词语时,一般隐含着临界问题,处理此类问题时,应把物理问题(或过程)推向极端,从而使临界现象(或状态)暴露出来,达到尽快求解的目的.
(2)假设法:有些物理过程中没有明显出现临界问题的线索,但在变化过程中可能出现临界问题,也可能不出现临界问题,解答此类题目,一般采用假设法.
此外,我们还可以应用图象法等进行求解.
1.临界问题的分析思路
解决临界问题的关键是:认真分析题中的物理情景,将各个过程划分阶段,找出各阶段中物理量发生突变或转折的“临界点”,然后分析出这些“临界点”应符合的临界条件,并将其转化为物理条件.
两类基本问题中,受力分析是关键,求解加速度是桥梁和枢纽,思维过程如下:
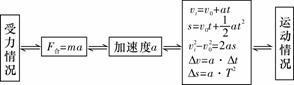
3.力和运动的关系
[例3]如图所示,弹簧左端固定,右端自由伸长到O点并系住物体m,现将弹簧压缩到A点,然后释放,物体一直可以运动到B点,如果物体受到的摩擦力恒定,则( )
A.物体从A到O加速,从O到B减速
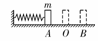 B.物体从A到O速度越来越小,从O到B加速度不变
B.物体从A到O速度越来越小,从O到B加速度不变
C.物体从A到O间先加速后减速,从O到B一直减速运动
D.物体运动到O点时所受合力为零
[错解]A;物体在O点附近来回运动,因此物体在O点的速度最大,则A选项正确.
[错因]犯以上错误的客观原因是思维定势,好像是弹簧振子的平衡位置O具有最大速度,这是盲目的模仿,主要是没有好的解题习惯,没有弄清楚力和运动的关系,另外有些同学是忽略了摩擦力.
[正解]在A点,弹簧弹力F大于摩擦力μmg,合外力向右,物体加速运动;在O点,弹簧弹力减小到零,只受摩擦力μmg,方向向左,物体在A到O之间一定存在某点弹力等于摩擦力,此时物体所受到的合外力为零,速度最大.故从A到O,物体先加速后减速,加速度先减小后增大.从O到B,合外力向左,物体一直减速运动,加速度一直增大,故C选项正确.
[答案]C
[思维提升]要正确理解力和运动的关系,物体运动方向和合外力方向相同时物体做加速运动,当弹力减小到等于摩擦力,即合外力为零时,物体的速度最大,小球的加速度决定于小球受到的合外力.
第 3 课时 牛顿运动定律的应用
重点难点突破
2.应用牛顿第二定律解题的基本方法
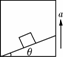
[例2]一物体放置在倾角为θ的斜面上,斜面固定于加速上升的电梯中,加速度为a,如图所示,在物体始终相对于斜面静止的条件下,下列说法正确的是( )
A.当θ一定时,a越大,斜面对物体的正压力 越小
越小
 B.当θ一定时,a越大,斜面对物体的摩擦力越大
B.当θ一定时,a越大,斜面对物体的摩擦力越大
C.当a一定时,θ越大,斜面对物体的正压力越小
D.当a一定时,θ越大,斜面对物体的摩擦力越小
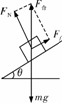 [解析]解法一:用合成法,根据平行四边形定则求解.对物体作受力分析,如图所示.(设物体质量为m,斜面对物体的正压力为FN,斜面对物体的摩擦力为Ff)物体具有向上的加速度a,由牛顿第二定律及力的合成有
[解析]解法一:用合成法,根据平行四边形定则求解.对物体作受力分析,如图所示.(设物体质量为m,斜面对物体的正压力为FN,斜面对物体的摩擦力为Ff)物体具有向上的加速度a,由牛顿第二定律及力的合成有
 -mg=ma
-mg=ma
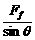 -mg=ma
-mg=ma
当θ一定时,a越大,FN越大,A不正确;当θ一定时,a越大,Ff越大,B正确;当a一定时,θ越大,FN越小,C正确;当a一定时,θ越大,Ff越大,D不正确.
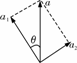 解法二:应用正交分解法求解.
解法二:应用正交分解法求解.
物体受重力、支持力、摩擦力的作用.由于支持力、摩擦力相互垂直,所以把加速度a在沿斜面方向和垂直于斜面方向分解,如图所示.
沿斜面方向,由牛顿第二定律得:
Ff-mgsin θ=masin θ ①
垂直于斜面方向,由牛顿第二定律得:
FN-mgcos θ=macos θ ②
当θ一定时,由①得,a越大,Ff越大,B正确.
由②得,a越大,FN越大,A错误.
当a一定时,由①得,θ越大,Ff越大,D错误.
由②得,θ越大,FN越小,C正确.
[答案]BC
[思维提升]解题方法要根据题设条件灵活选择.本题的解法二中,要分析的支持力和摩擦力相互垂直,所以分解加速度比较简单,但是当多数力沿加速度方向时,分解力比较简单.
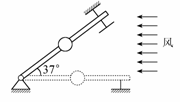 [拓展2]风洞实验中可产生水平方向的、大小可以调节的风力,先将一套有小球的细杆放入风洞实验室,小球孔径略大于细杆直径,如图所示.
[拓展2]风洞实验中可产生水平方向的、大小可以调节的风力,先将一套有小球的细杆放入风洞实验室,小球孔径略大于细杆直径,如图所示.
(1)当杆在水平方向上固定时,调节风力的大小,使小球在杆上匀速运动,这时所受风力为小球所受重力的0.5倍,求小球与杆的动摩擦因数;
(2)保持小球所受风力不变,使杆与水平方向间夹角为37°并固定,则小球从静止出发在细杆上滑下距离x的时间为多少.(sin 37°=0.6,cos 37°=0.8)
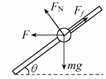 [解析](1)设小球所受的风力为F,支持力为FN、摩擦力为Ff、小球质量为m,作小球受力图,如图所示,当杆水平固定,即θ=0时,由题意得F=μmg
[解析](1)设小球所受的风力为F,支持力为FN、摩擦力为Ff、小球质量为m,作小球受力图,如图所示,当杆水平固定,即θ=0时,由题意得F=μmg
所以μ=F/mg=0.5mg/mg=0.5
(2)沿杆方向,由牛顿第二定律得
Fcos θ+mgsin θ-Ff=ma ①
在垂直于杆的方向,由共点力平衡条件得
FN+Fsin θ-mgcos θ=0 ②
又Ff=μFN ③
联立①②③式解得
a=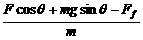 =
=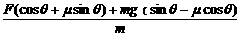
将F=0.5mg代入上式得a=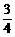 g ④
g ④
由运动学公式得x=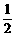 at2 ⑤
at2 ⑤
由④⑤式解得t=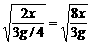
 易错门诊
易错门诊
1.瞬时性问题分析
[例1]如图甲所示,一质量为m的物体系于长度分别为L1、L2的两根细线上,L1的一端悬挂在天花板上,与竖直方向夹角为θ,L2水平拉直,物体处于平衡状态.
(1)现将L2线剪断,求剪断瞬间物体的加速度;
(2)若将图甲中的细线L1改为质量不计的轻弹簧而其余情况不变,如图乙所示,求剪断L2线瞬间物体的加速度.
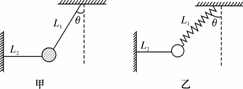
[解析](1)对图甲的情况,L2剪断的瞬间,绳L1不可伸缩,物体的加速度只能沿切线方向,则mgsin θ=ma1
所以a1=gsin θ,方向为垂直L1斜向下.
(2)对图乙的情况,设弹簧上拉力为FT1,L2线上拉力为FT2.重力为mg,物体在三力作用下保持平衡,有
FT1cos θ=mg,FT1sin θ=FT2,FT2=mgtan θ
剪断线的瞬间,FT2突然消失,物体即在FT2反方向获得加速度.因为mgtan θ=ma2,所以加速度a2=gtan θ,方向与FT2反向,即水平向右.
[思维提升](1)力和加速度的瞬时对应性是高考的重点.物体的受力情况应符合物体的运动状态,当外界因素发生变化(如撤力、变力、断绳等)时,需重新进行运动分析和受力分析,切忌想当然;
(2)求解此类瞬时性问题,要注意以下四种理想模型的区别:
|
特性 模型 |
质量 |
内部弹力 |
受外力时 的形变量 |
力能否突变 |
产生拉力或压力 |
|
轻绳 |
不计 |
处处相等 |
微小不计 |
可以突变 |
只有拉力没有压力 |
|
橡皮绳 |
较大 |
一般不能突变 |
只有拉力没有压力 |
||
|
轻弹簧 |
较大 |
一般不能突变 |
既可有拉力 也可有压力 |
||
|
轻杆 |
微小不计 |
可以突变 |
既有拉力也 可有支持力 |
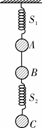 [拓展1]如图所示,弹簧S1的上端固定在天花板上,下端连一小球A,球A与球B之间用线相连.球B与球C之间用弹簧S2相连.A、B、C的质量分别为mA、mB、mC,弹簧与线的质量均不计.开始时它们都处于静止状态.现将A、B间的线突然剪断,求线刚剪断时A、B、C的加速度.
[拓展1]如图所示,弹簧S1的上端固定在天花板上,下端连一小球A,球A与球B之间用线相连.球B与球C之间用弹簧S2相连.A、B、C的质量分别为mA、mB、mC,弹簧与线的质量均不计.开始时它们都处于静止状态.现将A、B间的线突然剪断,求线刚剪断时A、B、C的加速度.
[解析]剪断A、B间的细线前,对A、B、C三球整体分析,弹簧S1中的弹力:
F1=(mA+mB+mC)g ①
方向向上.
对C分析,S2中的弹力:F2=mCg ②
方向向上.
剪断A、B间的细线时,弹簧中的弹力没变.
对A分析:F1-mAg=mAaA ③
对B分析:F2′+mBg=mBaB ④
对C分析:F2-mCg=mCaC ⑤
F2′=F2
由①③式解得aA=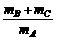 g,方向向上.
g,方向向上.
由②④式解得aB=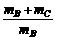 g,方向向下.
g,方向向下.
由②⑤式解得aC=0
3.物体的运动情况取决于物体受的力和物体的初始条件(即初速度),尤其是初始条件是很多同学最容易忽视的,从而导致不能正确地分析物体的运动过程.
 典例精析
典例精析
2.合力与速度同向时,物体加速,反之则减速.
分析力和运动关系问题时要注意以下几点:
1.物体所受合力的方向决定了其加速度的方向,合力与加速度的大小关系是F合=ma,只要有合力,不管速度是大还是小,或是零,都有加速度,只有合力为零时,加速度才能为零,一般情况下,合力与速度无必然的联系,只有速度变化才与合力有必然的联系.
2.当物体受多个力作用时,通常采用正交分解法.
为减少矢量的分解,建立坐标系,确定x轴正方向有两种方法:
(1)分解力不分解加速度,此时一般规定a方向为x轴正方向.
(2)分解加速度不分解力,此种方法以某种力的方向为x轴正方向,把加速度分解在x轴和y轴上.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com