
题目列表(包括答案和解析)
6.平衡物体的临界问题
(1)平衡物体的临界状态:物体的平衡状态 将要变化 的状态.
(2)临界条件:涉及物体临界状态的问题,解决时一定要注意 “恰好出现” 或 “恰好不出现” 等临界条件.
5.平衡物体的动态问题
(1)动态平衡:指通过控制某些物理量使物体的状态发生 缓慢变化 .在这个过程中物体始终处于 一系列平衡 状态中.
(2)动态平衡特征:一般为三力作用,其中一个力的大小和方向均不变化,一个力的大小 变化 而方向 不变 ,另一个力的大小和方向 均变化 .
4.求解平衡问题的一般步骤
(1)选对象:根据题目要求,选取某平衡体(整体或局部)作为研究对象.
(2)画受力图:对研究对象作受力分析,并按各个力的方向画出隔离体受力图.
(3)建坐标:选取合适的方向建立直角坐标系.
(4)列方程求解:根据平衡条件,列出合力为零的相应方程,然后求解,对结果进行必要的讨论.
3.共点力作用下物体的平衡条件
物体所受合外力为 零 ,即ΣF= 0 .若采用正交分解法求解平衡问题,则平衡条件应为ΣFx= 0 ,ΣFy= 0 .
2.平衡状态
物体处于 静止 或 匀速直线运动 状态称为物体处于平衡状态,平衡状态的实质是 加速度为零 的状态.
1.共点力
作用在物体的 同一点 或 作用线(或作用线的反向延长线)相交于一点 的几个力.
4.矢量图解法
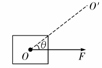 [例4]如图所示,物体静止于光滑水平面上,力F作用于物体O点,现要使物体沿着OO′方向做加速运动(F和OO′都在水平面内).那么,必须同时再加一个力F′,这个力的最小值是( )
[例4]如图所示,物体静止于光滑水平面上,力F作用于物体O点,现要使物体沿着OO′方向做加速运动(F和OO′都在水平面内).那么,必须同时再加一个力F′,这个力的最小值是( )
A.Fcos θ B.Fsin θ C.Ftan θ D.Fcot θ
[错解]当F′与F垂直时,F′最小,且F′=Fcot θ,所以选项D正确.
[错因]上述错误的原因是机械地套用两力垂直时力最小,而实际上本题中合力大小不定,方向确定.
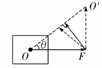 [正解]根据题意可知,F和F′的合力沿OO′方向,作出其矢量三角形,如图所示.由图可知,由F矢端向OO′作垂线,此垂线段即为F′的最小值,故F′的最小值为Fsin θ.
[正解]根据题意可知,F和F′的合力沿OO′方向,作出其矢量三角形,如图所示.由图可知,由F矢端向OO′作垂线,此垂线段即为F′的最小值,故F′的最小值为Fsin θ.
[答案]B
[思维提升]作出矢量三角形是解决此类问题的关键,同时要注意哪些力方向不变,哪些力大小、方向都不变.这类问题解决的方法是:大小和方向都改变的力向方向不变的力作垂线,该垂线长即为所求最小力.实际上也可以以F的矢端为圆心,以分力F′的大小为半径作圆,当圆与另一方向不变的力相切时,该半径即为所求力的最小值.
第 4 课时 共点力作用下物体的平衡
基础知识归纳
3. 平行四边形定则的应用
平行四边形定则的应用
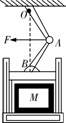
[例3]曲柄压榨机在食品工业、皮革制造等领域有着广泛的应用.如图是一曲柄压榨机的示意图.在压榨铰链A处作用的水平力为F,OB是铅垂线,OA、AB与铅垂线所夹锐角均为θ,假设杆重和活塞重可以忽略不计,求货物M在此时所受的压力为多大?
[解析]在图中铰链A处施加水平力F时,力F有两个作用效果,一是使杆AO受沿AO方向的压力FAO,二是使杆AB受沿AB方向的压力FAB,如图所示.
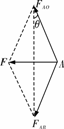 FAB=FAO,2FABsin θ=F,
FAB=FAO,2FABsin θ=F,
所以FAB=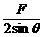
再将FAB分解为水平向左的分力Fx和竖直向下的分力Fy,则Fy的大小就是物体M所受压力的大小.
Fy=FABcos θ=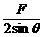 cos θ=
cos θ=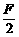 •cot θ
•cot θ
[思维提升]根据力产生的实际效果,分别对铰链A处和杆AB所受的力进行分解,求出物体M上所受的压力表达式.
 易错门诊
易错门诊
2.正交分解法
 [例2]已知共面的三个力F1=20 N,F2=30 N,F3=40 N,作用在物体的同一点上,三力之间的夹角都是120°,求合力的大小和方向.
[例2]已知共面的三个力F1=20 N,F2=30 N,F3=40 N,作用在物体的同一点上,三力之间的夹角都是120°,求合力的大小和方向.
[解析]建立如图所示的平面直角坐标系.
则Fx=F1x+F2x+F3=-F1sin 30°-F2sin 30°+F3
=(-20×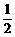 -30×
-30×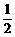 +40) N=15 N
+40) N=15 N
Fy=F1y+F2y=-F1cos 30°+F2cos 30°
=(-20× +30×
+30× ) N=5
) N=5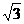 N
N
由图得F= N=10
N=10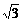 N
N
α=arctan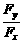 =arctan
=arctan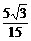 =30°
=30°
[思维提升]用正交分解法求多个力的合力的基本思路是:先将所有的力沿两个互相垂直的方向分解,求出这两个方向上的合力,再合成所得合力就是所有力的合力.
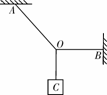 [拓展2]三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同,它们共同悬挂一重物,如图所示,其中OB是水平的,A端、B端固定.若逐渐增加C端所挂物体的质量,则最先断的绳( A )
[拓展2]三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同,它们共同悬挂一重物,如图所示,其中OB是水平的,A端、B端固定.若逐渐增加C端所挂物体的质量,则最先断的绳( A )
A.必定是OA B.必定是OB
C.必定是OC D.可能是OA,也可能是OC
根据平行四边形定则,利用邻边及其夹角跟对角线长短的关系分析力的大小变化情况的方法,通常叫做图解法.也可将平行四边形定则简化成三角形定则处理,更简单.图解法具有直观、简便的特点,多用于定性研究.应用图解法时应注意正确判断某个分力方向的变化情况及其空间范围.
用矢量三角形定则分析最小力的规律:
(1)当已知合力F的大小、方向及一个分力F1的方向时,另一个分力F2的最小条件是:两个分力垂直,如图甲.最小的F2=Fsin α.
(2)当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2最小的条件是:所求分力F2与合力F垂直,如图乙.最小的F2=F1sin α.
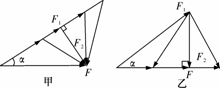
(3)当已知合力F的大小及一个分力F1的大小时,另一个分力F2最小的条件是:已知大小的分力F1与合力F同方向.最小的F2=|F-F1|.
 典例精析
典例精析
1. 受力分析
受力分析
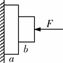
[例1]如图所示,物体b在水平推力F作用下,将物体a挤压在竖直墙壁上.a、b处于静止状态,对于a,b两物体的受力情况,下列说法正确的是( )
A.a受到两个摩擦力的作用 B.a共受到四个力的作用
C.b共受到三个力的作用 D.a受到墙壁的摩擦力的大小不随F的增大而增大
[解析]要使b处于平衡状态,a须对b产生一个竖直向上的摩擦力,则a受到b的摩擦力向下(大小等于b的重力),a要处于平衡状态,还要受到墙壁竖直向上的摩擦力,由整体受力平衡知此力大小不变.分析a、b的受力知它们分别受到5个、4个力的作用,综上所述可知A、D正确.
[答案] AD
[思维提升]在受力分析时,有些力的大小和方向不能确定,必须根据已经确定的几个力的情况和物体所处的状态判断出未确定的力的情况,以确保受力分析时不漏力、不添力、不错力.
 [拓展1]如图所示,位于斜面上的物体M在沿斜面向上的力F作用下而处于静止状态,对M的受力情况,下列说法正确的是( AB )
[拓展1]如图所示,位于斜面上的物体M在沿斜面向上的力F作用下而处于静止状态,对M的受力情况,下列说法正确的是( AB )
A.可能受三个力作用 B.可能受四个力作用
C.一定受三个力作用 D.一定受四个力作用
[解析]对M进行分析,受重力.M与斜面、外界F接触,与斜面挤压,F推M.与斜面挤压处是否有摩擦,是沿斜面向上还是沿斜面向下由F与mgsin α决定.所以A、B正确.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com