
题目列表(包括答案和解析)
3.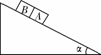 (2008•全国Ⅱ)如图,一固定斜面上两个质量相同的小物块A和B紧挨着匀速下滑,A与B的接触面光滑.已知A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角为α.B与斜面之间的动摩擦因数是( A )
(2008•全国Ⅱ)如图,一固定斜面上两个质量相同的小物块A和B紧挨着匀速下滑,A与B的接触面光滑.已知A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍,斜面倾角为α.B与斜面之间的动摩擦因数是( A )
A.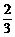 tan α
B.
tan α
B.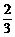 cot α C.tan
α D.cot α
cot α C.tan
α D.cot α
2.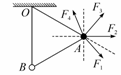 (2007•上海)如图所示,用两根细线把A、B两小球悬挂在天花板上的同一点O,并用第三根细线连接A、B两小球,然后用某个力F作用在小球A上,使三根细线均处于直线状态,且OB细线恰好沿竖直方向,两小球均处于静止状态.则该力可能为图中的( BC )
(2007•上海)如图所示,用两根细线把A、B两小球悬挂在天花板上的同一点O,并用第三根细线连接A、B两小球,然后用某个力F作用在小球A上,使三根细线均处于直线状态,且OB细线恰好沿竖直方向,两小球均处于静止状态.则该力可能为图中的( BC )
A.F1 B.F2 C.F3 D.F4
[解析]因OB线处于竖直状态,对小球B受力分析,可知小球A、B间的细线没有弹力,故小球A受到重力、OA细线的拉力及力F三个力的作用处于平衡状态,由共点力的平衡条件推论可知,力F的方向位于重力和OA拉力的合力反方向,因此力F可能位于图中的F2或F3或竖直向上(此时F等于重力,OA线拉力为零).故正确的选项为B、C.
1.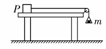 (2007•海南)如图,P是位于水平的粗糙桌面上的物块.用跨过定滑轮的轻绳将P与小盘相连,小盘内有砝码,小盘与砝码的总质量为m.在P运动的过程中,若不计空气阻力,则关于P在水平方向受到的作用力与相应的施力物体,下列说法正确的是( B )
(2007•海南)如图,P是位于水平的粗糙桌面上的物块.用跨过定滑轮的轻绳将P与小盘相连,小盘内有砝码,小盘与砝码的总质量为m.在P运动的过程中,若不计空气阻力,则关于P在水平方向受到的作用力与相应的施力物体,下列说法正确的是( B )
A.拉力和摩擦力,施力物体是地球和桌面
B.拉力和摩擦力,施力物体是绳和桌面
C.重力mg和摩擦力,施力物体是地球和桌面
D.重力mg和摩擦力,施力物体是绳和桌面
3.共点力作用下物体平衡问题的求解方法
求解平衡问题的基本方法是力的合成法和分解法,同时也要注意以下方法的灵活运用.
(1)整体法和隔离法:把发生相互作用的几个物体组成的系统看做整体考虑,分析其受力情况及运动情况的方法称为整体法;而把系统中某个物体或某几个物体从系统中隔离出来,分析其受力情况及运动情况的方法称为隔离法.在选取研究对象时,整体法和隔离法是常用的方法,要灵活选择.
(2)正交分解法:把物体受到的外力沿正交的x轴和y轴方向进行分解,由于物体处于平衡状态,则物体在x、y轴方向上的合外力均为零,表达式为:Fx合=0,Fy合=0.
(3)矢量三角形:若三个不平行的共点力的合力为零,三力矢量平移组成的图形必定为一封闭的三角形.
(4)三力汇交原理:物体在同一平面内的三个不平行的力的作用下处于平衡状态,这三个力必定共点.
(5)相似三角形法:对于受到三个共点力的作用而处于平衡状态的物体来说,这三个力可构成一个封闭的矢量三角形,我们可运用数学中解三角形的有关知识来求解.如正弦、余弦定理.有时还可以利用力的矢量三角形与物体所在空间构成的几何三角形的相似来求解.
(6)图解法:这种方法适用于三力平衡或力的分解、合成中已知一个力的大小、方向不变,另一个力的方向不变,判断因第三个力的变化而引起两个力大小变化的情况,以及另一个力的大小不变、方向改变而引起第三个力的变化情况.
(7)假设法(或极限法):当物体受几个力作用,出现临界现象(平衡状态恰好出现变化或恰好不出现变化)时采用,即把某个没有给定数值的力推向极端(极大或极小)来分析,从而得出“恰好出现”或“恰好不出现”的结果.
高考真题赏析
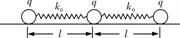 [例1](2009•浙江)如图所示,在光滑绝缘水平面上放置3个电荷量均为q(q>0)的相同小球,小球之间用劲度系数均为k0的轻质弹簧绝缘连接.当3个小球处在静止状态时,每根弹簧长度为l.已知静电力常量为k,若不考虑弹簧的静电感应,则每根弹簧的原长为( )
[例1](2009•浙江)如图所示,在光滑绝缘水平面上放置3个电荷量均为q(q>0)的相同小球,小球之间用劲度系数均为k0的轻质弹簧绝缘连接.当3个小球处在静止状态时,每根弹簧长度为l.已知静电力常量为k,若不考虑弹簧的静电感应,则每根弹簧的原长为( )
A.l+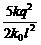 B.l-
B.l-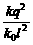 C.l-
C.l-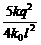 D.l-
D.l-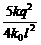
[考点]与弹簧弹力大小计算相关的平衡问题.
[解析]对最左边的带电小球进行受力分析,小球受到中间小球对其的斥力,最右边小球对其的斥力以及弹簧对其的拉力,然后根据平衡条件列方程,可得k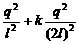 =k0(l-l0),解得l0=l-
=k0(l-l0),解得l0=l-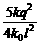
[答案]C
[思维提升]对弹簧而言,弹簧弹力F=kx,特别注意其中的x为弹簧的形变量,而不是弹簧的长度,弹簧如果处于伸长状态,则x=l-l0;弹簧如果处于压缩状态,则x=l0-l,其中l0为弹簧原长.本题综合了电学知识,正确的受力分析是求解本题的关键.
 [例2](2009•北京)如图所示,将质量为m的滑块放在倾角为θ的固定斜面上.滑块与斜面之间的动摩擦因数为μ.若滑块与斜面之间的最大静摩擦力和滑动摩擦力大小相等,重力加速度为g,则( )
[例2](2009•北京)如图所示,将质量为m的滑块放在倾角为θ的固定斜面上.滑块与斜面之间的动摩擦因数为μ.若滑块与斜面之间的最大静摩擦力和滑动摩擦力大小相等,重力加速度为g,则( )
A.将滑块由静止释放,如果μ>tan θ,滑块将下滑
B.给滑块沿斜面向下的初速度,如果μ<tan θ,滑块将减速下滑
C.用平行于斜面向上的力拉滑块向上匀速滑动,如果μ=tan θ,拉力大小应是2mgsin θ
D.用平行于斜面向下的力拉滑块向下匀速滑动,如果μ=tan θ,拉力大小应是mgsin θ
[考点]摩擦力的方向判断及大小计算.
[解析]对滑块进行受力分析,将滑块由静止释放,如果μ>tan θ,则滑块在沿斜面方向上受到的重力的分力G1=mgsin θ,而滑块与斜面间的最大静摩擦力为fmax=μmgcos θ>
tan θ•mgcos θ=mgsin θ,故滑块不会向下滑动,A错误;给滑块沿斜面向下的初速度,如果μ<tan θ,则滑块在沿斜面方向上受到的重力的分力为G1=mgsin θ,而滑块与斜面间的最大静摩擦力为fmax=μmgcos θ<tan θ•mgcos θ=mgsin θ,故滑块所受合外力一定沿斜面向下,滑块将加速下滑,B错误;用平行于斜面向上的力拉滑块向上匀速运动,如果μ=tan θ,则拉力F=mgsin θ+μmgcos θ=2mgsin θ,故C正确;同理可知D错误.
[答案]C
[思维提升]解答有关摩擦力大小问题时,一定要先判断物体所受的摩擦力是静摩擦力还是滑动摩擦力,然后根据公式Ff=μFN,或平衡条件,或牛顿运动定律求解计算.
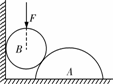 [例3](2008•天津)在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体A,A与竖直墙之间放一光滑圆球B,整个装置处于静止状态.现对B加一竖直向下的力F,F的作用线通过球心,设墙对B的作用力为F1,B对A的作用力为F2,地面对A的作用力为F3,若F缓慢增大而整个装置仍保持静止,截面积如图所示,在此过程中( )
[例3](2008•天津)在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体A,A与竖直墙之间放一光滑圆球B,整个装置处于静止状态.现对B加一竖直向下的力F,F的作用线通过球心,设墙对B的作用力为F1,B对A的作用力为F2,地面对A的作用力为F3,若F缓慢增大而整个装置仍保持静止,截面积如图所示,在此过程中( )
A.F1保持不变,F3缓慢增大 B.F1缓慢增大,F3保持不变
C.F2缓慢增大,F3缓慢增大 D.F2缓慢增大,F3保持不变
[考点]力的合成与分解、平衡条件、整体法和隔离法等.
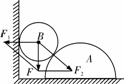 [解析]力F产生了两个作用效果,一个是使B压紧墙面的力F1,一个是压紧A的力F2,当力F缓慢增大时,合力的方向和两个分力的方向都没有发生变化,所以当合力增大时两个分力同时增大.用整体法进行分析,可知地面对A的作用力F3是弹力与摩擦力的合力,摩擦力与F1大小相等,方向相反;弹力与力F和两球重力的合力大小相等,方向相反,C正确.
[解析]力F产生了两个作用效果,一个是使B压紧墙面的力F1,一个是压紧A的力F2,当力F缓慢增大时,合力的方向和两个分力的方向都没有发生变化,所以当合力增大时两个分力同时增大.用整体法进行分析,可知地面对A的作用力F3是弹力与摩擦力的合力,摩擦力与F1大小相等,方向相反;弹力与力F和两球重力的合力大小相等,方向相反,C正确.
[答案]C
[思维提升]求解平衡问题的方法较多,一般方法为整体法和隔离法、合成法和分解法,高考试题十分注重对基本方法的考查.
高考试题选编
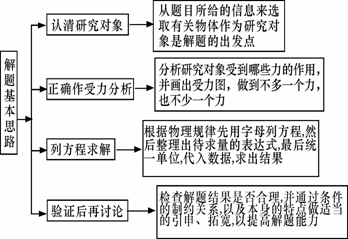
2.分析共点力作用下物体平衡问题的基本思路
1.摩擦力的方向判断和大小计算方法
(1)摩擦力的方向总是沿着接触面,并且跟物体相对运动的方向或相对运动趋势的方向相反,所谓相对运动或相对运动趋势,参考对象是跟研究对象相接触的物体.相对运动趋势的方向可由假设法判定:假设接触面间光滑,物体相对运动的方向即为不光滑时相对运动趋势的方向.
(2)求解摩擦力之前先分清是滑动摩擦力还是静摩擦力(即先分“动”、“静”),如果是滑动摩擦力,用公式Ff=μFN求解;如果是静摩擦力,应根据物体所处的运动状态,由力的平衡条件或牛顿运动定律求解.
3.“验证力的平行四边形定则”实验注意事项
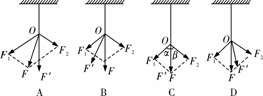
[例3]如图所示,是两位同学在研究“验证力的平行四边形定则”时所得到的实验结果,若F′的作用效果与F1、F2共同作用效果相同,则尊重实验事实的结果为( )
[错解一]F为F1、F2的合力,因此A、B、D均有可能.
[错解二]只要认真完成实验,误差可以被消除,C正确.
[错因]F′为用一只弹簧秤拉时弹簧秤的拉力,其方向一定沿橡皮条方向,B、D选项不满足要求.误差只能减少,不可能被消除,C错误.
[正解]F′一定沿橡皮条伸长方向,故B、D错误.C是硬凑数据,事实上,实验要有一定事实上的误差,包括大小和方向,故A正确.
[答案]A
[思维提升]在做实验题的时候应该尊重实验事实,不可以想当然.在复习实验时重点是理解实验原理和掌握实验方法,特别是实验原理,任何变化都离不开实验原理,要注意从原理出发找方法、选器材、定方案.
第 6 课时 单元综合提升
知识网络构建

经典方法指导
本部分的处理:对力的处理方式上要灵活运用力的合成和分解,在研究对象的选取角度上要灵活运用隔离法和整体法,而共点力的平衡问题又常常选取与重力、弹力、摩擦力相关而且与实际情景相结合的背景.其中摩擦力的大小、方向又是高考考查的一个热点,应给予格外关注.
2.实验:验证力的平行四边形定则
[例2]在“验证力的平行四边形定则”的实验中
(1)其中两个实验步骤分别是
A.在水平放置的方木板上固定一张白纸,用图钉把橡皮条的一端固定在方木板上,另一端拴上两个绳套,通过细绳的同时用两个弹簧测力计(弹簧测力计与方木板平面平行)互成角度地拉橡皮条,使它与细绳的结点到达某一位置O点,在白纸上用铅笔记下O点的位置并读出两个弹簧测力计的示数F1和F2.
B.只用一只弹簧测力计,通过细绳拉橡皮条,使它的伸长量与两个弹簧测力计拉时相同,读出此时弹簧测力计的示数F′并记下细绳的方向.
请指出以上步骤中的错误或疏漏:A中是 ;B中是 .
(2)在某次实验中,两个弹簧测力计的拉力F1、F2已在图中画出,图中的方格的边长表示为2 N,O点是橡皮条的结点,请用两个直角三角板严格作出合力F的图示,并求出合力的大小为 N.
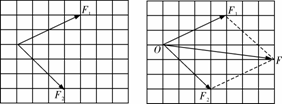
[解析]当用两个弹簧测力计互成角度地拉橡皮条,使它与细绳的结点到达某一位置O点,在白纸上用铅笔记下O点的位置,读出两个弹簧测力计的示数F1和F2及记下此时两细绳套的方向.
当只用一只弹簧测力计拉时,应使结点拉到同样的位置O,并记下弹簧测力计的读数和细绳的方向.
[答案](1)未记下两条细绳的方向;应将橡皮条与细绳的结点拉到原来的位置O点 (2)10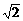
[思维提升]对于验证的平行四边形定则的实验,要在熟悉实验原理、掌握实验过程的基础上,理解并记忆相关的注意事项,否则就会出现错误.用图象法处理实验数据时,重在规范作图.
[拓展2]请不用弹簧秤,只用三条相同的橡皮条、四个图钉、一把直尺和一支铅笔、三张白纸、平木板来验证平行四边形定则.
[解析]仅用橡皮条也可验证平行四边形定则,其步骤、方法如下:
 (1)将三条橡皮条的一端都拴在一个图钉O上,将这三条橡皮条的另一端分别再拴一个图钉A、B、C,注意此时四个图钉均未固定在板上,如图所示.
(1)将三条橡皮条的一端都拴在一个图钉O上,将这三条橡皮条的另一端分别再拴一个图钉A、B、C,注意此时四个图钉均未固定在板上,如图所示.
(2)用直尺测出橡皮条的自由长度L0,注意从图钉脚之间测起.
(3)将拴有橡皮条的图钉A、B适当张开钉在木板上,拉第三根橡皮条C,即使三条橡皮条互成角度拉伸,待节点处的图钉O静止时,钉下C图钉,并记录图钉O的位置(注意此时O图钉不能钉)记录图钉A、B、C的位置.(此时图钉有孔,不需铅笔)
(4)测出这三条橡皮条的长度L1、L2、L3,分别算出它们的伸长量X1=L1-L0,X2=L2-L0,X3=L3-L0
(5)将X1、X2、X3按一定比例图示出来,以X1、X2为邻边作平行四边形,求出其对角线OC′.比较OC′与OC的长度(即X3的长度),如果相等,且在一条直线上,则达到目的,若OC′与OC有一微小夹角θ,则有误差(如上图所示).
本实验是根据图钉O受到三个平面共点力而静止,任意两个力的合力与第三个力大小相等方向相反的原理.
 易错门诊
易错门诊
1.实验:探究弹力与弹簧伸长的关系
[例1]某同学用如图所示装置做探究弹力和弹簧伸长关系的实验.他先测出不挂钩码时弹簧下端指针所指的标尺刻度,然后在弹簧下端挂上砝码,并逐个增加砝码,测出指针所指的标尺刻度,所得数据列表如下:(重力加速度g取9.8 m/s2)
|
砝码质量 m/102 g |
0 |
1.00 |
2.00 |
3.00 |
4.00 |
5.00 |
6.00 |
7.00 |
|
标尺刻度 x/10-2 m |
15.00 |
18.94 |
22.82 |
26.78 |
30.66 |
34.60 |
42.00 |
54.50 |
(1)根据所测数据,在图坐标纸上作出弹簧指针所指标尺刻度x与砝码质量m的关系曲线.
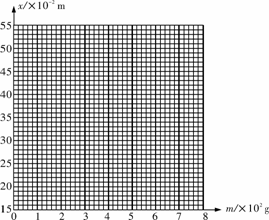
(2)根据所测得数据和关系曲线可以判断,在 范围内弹力大小与弹簧伸长关系满足胡克定律.这种规格的弹簧劲度系数为 N/m.
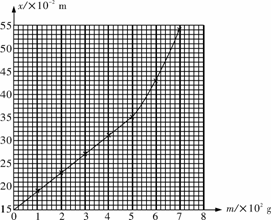 [解析](1)根据表中数据描点,按照各点的分布与走向,作出一条平滑曲线,如图所示.
[解析](1)根据表中数据描点,按照各点的分布与走向,作出一条平滑曲线,如图所示.
(2)由关系曲线可以看出,砝码质量在0-500 g范围内,图线近似为一条直线,即满足弹簧的拉力和形变量成正比(胡克定律).当不挂砝码时,弹簧的长度l0=15×10-2 m.当砝码质量
m=500 g时,l≈35×10-2
m,由ΔF=mg=kΔx解得k=mg/(l-l0)=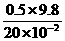 N/m=25 N/m
N/m=25 N/m
[答案](1)见解析 (2)0-500 g;25
[思维提升](1)据所给实验数据描点,然后作出平滑曲线(或直线),注意所画的线不一定过所有点,原则是应尽量使各点较均匀地分布在曲线(或直线)的两侧,描点时要符合客观实际,“曲”、“直”分明.(2)理解坐标的物理含义:x为挂不同砝码时弹簧的长度而不是形变量.(3)曲线的弯曲部分表示弹力超过了弹簧的弹性限度.
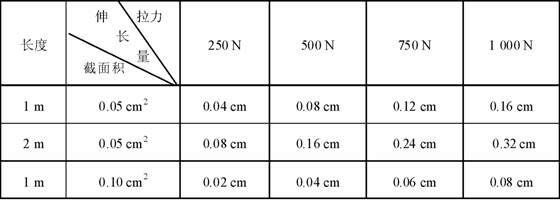 [拓展1]用金属制成的线材(如钢丝、钢筋)受到拉力会伸长,十七世纪英国物理学家胡克发现:金属丝或金属杆在弹性限度内它的伸长与拉力成正比,这就是著名的胡克定律.这一发现为后人对材料的研究奠定了重要基础.现有一根用新材料制成的金属杆,长为4 m,横截面积为0.8 cm2,设计要求它受到拉力后伸长不超过原长的1/1 000,问最大拉力多大?由于这一拉力很大,杆又较长,直接测试有困难,选用同种材料制成样品进行测试,通过测试取得数据如下:
[拓展1]用金属制成的线材(如钢丝、钢筋)受到拉力会伸长,十七世纪英国物理学家胡克发现:金属丝或金属杆在弹性限度内它的伸长与拉力成正比,这就是著名的胡克定律.这一发现为后人对材料的研究奠定了重要基础.现有一根用新材料制成的金属杆,长为4 m,横截面积为0.8 cm2,设计要求它受到拉力后伸长不超过原长的1/1 000,问最大拉力多大?由于这一拉力很大,杆又较长,直接测试有困难,选用同种材料制成样品进行测试,通过测试取得数据如下:
(1)测得结果表明材料受拉力作用后,其伸长量与材料的长度成 正比 ,与材料的截面积成 反比 .
(2)上述金属细杆承受的最大拉力为 104 N.
[解析](1)由题中列表可看出,材料样品的伸长量与材料的长度成正比,与材料的截面积成反比.
(2)由表可看出,材料一定长、一定截面积时,拉力与伸长量的比例为定值.
设1 m长,截面积为0.05 cm 2的比例系数为K1;
2 m长,截面积为0.05 cm2的比例系数为K2;
1 m长,截面积为0.10 cm2的比例系数为K3.
则K1=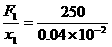 N/m=6.25×105 N/m
N/m=6.25×105 N/m
K2=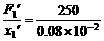 N/m=
N/m= ×6.25×105
N/m
×6.25×105
N/m
K3=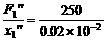 N/m=2×6.25×105 N/m
N/m=2×6.25×105 N/m
由K1、K2、K3的值可得,比例系数K与长度L成反比,与截面积S成正比,故K∝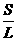
设4 m长,截面积为0.8 cm2的比例系数为K0,
则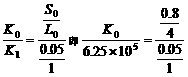
所以K0=2.5×106 N/m
又金属细杆最大伸长量为xm=4×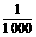 m=4×10-3
m
m=4×10-3
m
所以金属细杆承受的最大拉力为
Fm=K0xm=2.5×106×4×10-3 N=104 N
3.误差分析
本实验误差的主要来源除弹簧秤本身的误差外,还出现读数误差、作图误差,因此读数时眼睛一定要正视,要按有效数字正确读数和记录,两力的对边要平行.两个分力F1和F2间的夹角θ越大,用平行四边形作图得出的合力F的误差ΔF也越大,所以实验中不要把θ取得太大.但也不宜太小,以60°-100°之间为宜.

 典例精析
典例精析
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com