
题目列表(包括答案和解析)
例:在光滑水平长直轨道上,放着一个静止的弹簧振子,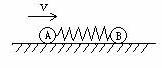 它由一轻弹簧两端各联结一个小球构成,两小球质量相等,现突然给左端小球一个向右的速度V,试分析从开始运动到弹簧第一次恢复原长这一过程中两球的运动情况并求弹簧第一次恢复到自然长度时,每个小球的速度?
它由一轻弹簧两端各联结一个小球构成,两小球质量相等,现突然给左端小球一个向右的速度V,试分析从开始运动到弹簧第一次恢复原长这一过程中两球的运动情况并求弹簧第一次恢复到自然长度时,每个小球的速度?
[析与解]:刚开始,A向右运动,B静止,A、B间距离减小,弹簧被压缩,对两球产生斥力,相当于一般意义上的碰撞,此时A动量减小,B动量增加。当两者速度相等时,两球间距离最小,弹簧形变量最大。接着,A、B不会一直做匀速直线运动,弹簧要恢复原长,对两球产生斥力,A动量继续减小,B动量继续增加。所以,到弹簧第一次恢复原长时,A球动量最小,B球动量最大。
在整个过程中,系统动量守恒,从开始到第一次恢复原长时,弹簧的弹性势能均为零,即系统的动能守恒。
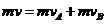
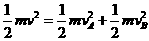
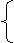 解得:
解得: 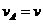
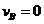 (这组解即为刚开始两个物体的速度)
(这组解即为刚开始两个物体的速度)
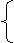 或
或 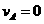
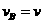 (此组解为弹簧第一次恢复原长时两个物体的速度)
(此组解为弹簧第一次恢复原长时两个物体的速度)
当然,读者还可以继续讨论接下来两个物体的运动情况。
实际上,不管 是一般意义上的碰撞,还是类碰撞,在相互作用时两个物体的受力情况、冲量方向及动量变化情况是学生处理这类问题的难点所在。下面作者再补充一些相关习题作巩固用
是一般意义上的碰撞,还是类碰撞,在相互作用时两个物体的受力情况、冲量方向及动量变化情况是学生处理这类问题的难点所在。下面作者再补充一些相关习题作巩固用
1、甲、乙两球在光滑水平面上,在同一直线同一方向上运动,它们的动量分别为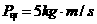 ,
,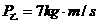 。已知甲的速度大于乙的速度,甲球与乙球相碰,碰撞后乙球的动量变为
。已知甲的速度大于乙的速度,甲球与乙球相碰,碰撞后乙球的动量变为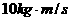 ,则甲、乙两球质量
,则甲、乙两球质量 和
和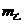 的关系为
的关系为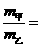 。
。
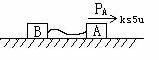 例:如图所示,光滑水平面上有两个质量相等的物体,其间用一不可伸长的细绳相连,开始B静止,A具有
例:如图所示,光滑水平面上有两个质量相等的物体,其间用一不可伸长的细绳相连,开始B静止,A具有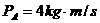 (规定向右为正)的动量,开始绳松弛,那么在绳拉紧的过程中,A、B动量变化可能是( )
(规定向右为正)的动量,开始绳松弛,那么在绳拉紧的过程中,A、B动量变化可能是( )
A、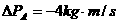 ,
,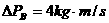
B、 ,
,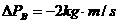
C、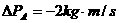 ,
,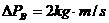
D、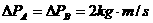
[析与解]:绳模型中两物体组成的系统同样要满足上述的三个原则,只是在第2个原则中,由于绳对两个小球施加的是拉力,前者受到的冲量向后,动量减小;后者受到的冲量向前,动量增加,当两者的速度相等时,绳子的拉力为零,一起做匀速直线运动。综上所述,本题应该选择C选项。
3、系统能量守恒原则:在碰撞中,若没有能量损耗,则系统机械能守恒;若能量有损失,则系统的机械能减小;而系统的机械能不可能增加。一般而言,碰撞中的重力势能不变, 所以有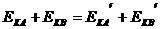 。此题中D选项可以排除。
。此题中D选项可以排除。
综上所述,本题正确答案为(A、C)
2、物理情景可行性原则:
(1)、碰撞前,A追上B发生碰撞,所以有碰前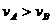
(2)、碰撞时,两球之间是斥力作用,因此前者受到的冲量向前,动量增加;后者受到的冲量向后,动量减小,既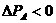 ,
,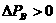 。此题B选项可以排除
。此题B选项可以排除
(3)、碰撞后,A球位置在后,所以有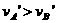
1、 统动量守恒原则:即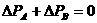 。此题ABCD选项均符合
。此题ABCD选项均符合
3、一般的碰撞:碰撞时产生的形变有部分恢复,此时系统动量守恒但机械能有部分损失。
例:在光滑水平面上A、B两球沿同一直线向右运动,A追上B发生碰撞,碰前两球动量分别为 、
、 ,则碰撞过程中两物体的动量变化可能的是( )
,则碰撞过程中两物体的动量变化可能的是( )
A、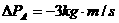 ,
,
B、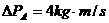 ,
,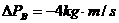
C、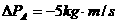 ,
,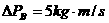
D、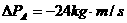 ,
,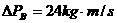
[析与解]:碰撞中应遵循的原则有:
2、完全非弹性碰撞:碰撞后物体粘结成一体或相对静止,即相互碰撞时产生的形变一点没有恢复,碰撞后相互作用的物体具有共同速度,系统动量守恒,但系统的机械能不守恒,此时损失的最多。
如图所示,光滑水平面上两个质量分别为m1、m2小球相碰。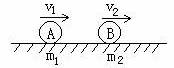 这种碰撞可分为正碰和斜碰两种,在高中阶段只研究正碰。正碰又可分为以下几种类型:
这种碰撞可分为正碰和斜碰两种,在高中阶段只研究正碰。正碰又可分为以下几种类型:
1、完全弹性碰撞:碰撞时产生弹性形变,碰撞后形变完全消失,碰撞过程系统的动量和机械能均守恒
6.如图所示,两个完全相同质量为m 的木板A、B 置于水平面上。它们的间距s=2.88m,质量为2m、大小可以忽略的物块C 置于A 板的左端。C 与A 之间的动摩擦因数为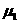 =0.22,A、B 与水平面之间的动摩擦因数
=0.22,A、B 与水平面之间的动摩擦因数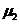 =0.10,最大静摩擦力可认为等于滑动摩擦力。开始时,三个物体处于静止状态,现给C 施加一个水平向右,大小为
=0.10,最大静摩擦力可认为等于滑动摩擦力。开始时,三个物体处于静止状态,现给C 施加一个水平向右,大小为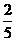 mg的恒力F,假定A、B 碰撞时间很短且碰撞后粘连在一起,要使C 最终不脱离木板,每块木板的长度最少要为多少?
mg的恒力F,假定A、B 碰撞时间很短且碰撞后粘连在一起,要使C 最终不脱离木板,每块木板的长度最少要为多少?
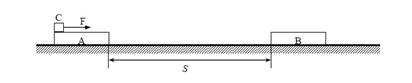
解析:在A,B碰撞之前,A,C间的最大静摩擦力为2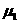 mg=0.44mg,大于C所受到的外力0.4mg,因此,A,C之间无相对运动。所以A,C可作为一个整体。碰撞前A,C的速度可以用动能定理求出。
mg=0.44mg,大于C所受到的外力0.4mg,因此,A,C之间无相对运动。所以A,C可作为一个整体。碰撞前A,C的速度可以用动能定理求出。
碰撞之后,A,B具有共同的速度,C的速度不变。A,C间发生相对运动。并且根据题意,A,B,C系统所受的摩擦力等于F,因此系统所受的合外力为零。可运用动量守恒定理求出C刚好不脱离木板的系统最终的共同速度。然后,运用能量守恒定律求出A,B的长度,即C与A,B发生相对位移的距离。
由于F小于A,C间最大静摩擦力,所以A,C无相对运动。
FS-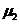 3mgS=
3mgS=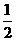 3m
3m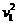
解得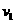 =
=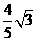 m/s
m/s
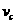 =
=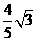 m/s,m
m/s,m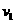 =2m
=2m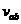
得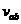 =
=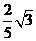 m/s
m/s
因为,F=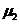 4mg=0.4mg;所以,A,B,C组成的系统合外力为零
4mg=0.4mg;所以,A,B,C组成的系统合外力为零
2m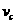 +2m
+2m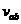 =4m
=4m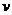
得,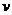 =
=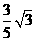 m/s
m/s
由能量守恒定理得
F2L+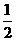 4m
4m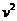 -
-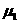 2mg2L=
2mg2L=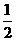 2m
2m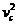 +
+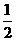 2m
2m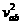
L=5m
5. 在绝缘水平面上放一质量m=2.0×10-3kg的带电滑块A,所带电荷量q=1.0×10-7C.在滑块A的左边l=0.3m处放置一个不带电的绝缘滑块B,质量M=4.0×10-3kg,B与一端连在竖直墙壁上的轻弹簧接触(不连接)且弹簧处于自然状态,弹簧原长S=0.05m.如图所示,在水平面上方空间加一水平向左的匀强电场,电场强度的大小为E=4.0×105N/C,滑块A由静止释放后向左滑动并与滑块B发生碰撞,设碰撞时间极短,碰撞后两滑块结合在一起共同运动并一起压缩弹簧至最短处(弹性限度内),此时弹性势能E0=3.2×10-3J,两滑块始终没有分开,两滑块的体积大小不计,与水平面间的动摩擦因数均为μ=0.5,g取10m/s2.求:
在绝缘水平面上放一质量m=2.0×10-3kg的带电滑块A,所带电荷量q=1.0×10-7C.在滑块A的左边l=0.3m处放置一个不带电的绝缘滑块B,质量M=4.0×10-3kg,B与一端连在竖直墙壁上的轻弹簧接触(不连接)且弹簧处于自然状态,弹簧原长S=0.05m.如图所示,在水平面上方空间加一水平向左的匀强电场,电场强度的大小为E=4.0×105N/C,滑块A由静止释放后向左滑动并与滑块B发生碰撞,设碰撞时间极短,碰撞后两滑块结合在一起共同运动并一起压缩弹簧至最短处(弹性限度内),此时弹性势能E0=3.2×10-3J,两滑块始终没有分开,两滑块的体积大小不计,与水平面间的动摩擦因数均为μ=0.5,g取10m/s2.求:
(1)两滑块碰撞后刚结合在一起的共同速度v;
(2)两滑块被弹簧弹开后距竖直墙壁的最大距离s.
解析:(1)设两滑块碰前A的速度为v1,由动能定理有:
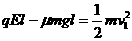
解得:v1=3m/s
A、B两滑块碰撞,由于时间极短动量守恒,设共同速度为v
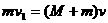
解得:v=1.0m/s
(2)碰后A、B一起压缩弹簧至最短,设弹簧压缩量为x1,由动能定理有:
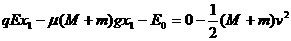
解得:x1=0.02m
设反弹后A、B滑行了x2距离后速度减为零,由动能定理得:

解得:x2≈0.05m
以后,因为qE>μ(M+m)g,滑块还会向左运动,但弹开的距离将逐渐变小,所以,最大距离为:
S=x2+s-x1=0.05m+0.05m-0.02m=0.08m.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com