
题目列表(包括答案和解析)
5. (2010·济南实验中学模拟)(1)现要验证“当质量一定时,物体运
(2010·济南实验中学模拟)(1)现要验证“当质量一定时,物体运
动的加速度与它所受的合外力成正比”这一物理规律.给定的
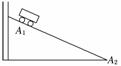
器材如下:一倾角可以调节的长斜面(如图实-4-10所示)、
小车、计时器一个、米尺. 图实-4-10
(1)填入适当的公式或文字,完善以下实验步骤(不考虑摩擦力的影响):
①让小车自斜面上方一固定点A1从静止开始下滑至斜面底端A2,记下所用的时间t.
②用米尺测量A1与A2之间的距离x,则小车的加速度a=________.
③用米尺测量A1相对于A2的高度h.设小车所受重力为mg,则小车所受合外力F=
_______.
④改变________________________,重复上述测量.
⑤以h为横坐标,1/t2为纵坐标,根据实验数据作图.如能得到一条过原点的直线,则可以验证“当质量一定时,物体运动的加速度与它所受的合外力成正比”这一规律.
(2)在“验证牛顿运动定律”的实验中,实验装置如图实-4-11甲所示,有一位同学通过实验测量作出了图乙中的A图线.试分析:
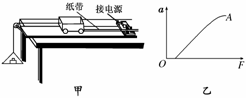
图实-4-11
①A图线不通过坐标原点的原因是__________________________________________;
②A图线上部弯曲的原因是________________________________________________.
解析:(1)②由x=at2可得:a=.
③sinθ=,不计摩擦力时,小车的合外力F=mgsinθ=mg.
④小车的质量不变,要改变小车所受的合外力F重做上述实验时,只要改变斜面的倾角(或A1、A2两点间的高度h的数值)即可.
(2)①图线在F轴上有截距,说明没有平衡摩擦力或平衡摩擦力不够.
②a-F图线上部弯曲的原因是未满足钩码质量远小于小车质量.
答案:(1)② ③mg ④斜面倾角(或h的数值)
(2)①没有平衡摩擦力或平衡摩擦力不够
②未满足钩码质量远小于小车质量
4.(2010·广州联考)某同学在做加速度和力、质量的关系的实验中,测得小车的加速度a和拉力F的数据如下表所示:
|
F/N |
0.20 |
0.30 |
0.40 |
0.50 |
0.60 |
|
a/(m·s-2) |
0.11 |
0.19 |
0.29 |
0.40 |
0.51 |
(1)根据表中的数据在图实-4-9所示的坐标中作出a-F图象;

图实-4-9
(2)图象的斜率的物理意义是_______________________________________________;
(3)图象(或延长线)与F轴的截距的物理意义是________________________;
(4)小车和砝码的总质量为________ kg.
解析:(1)选取适当的标度,作出a-F图象如图所示.
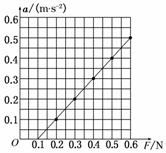
(2)由F=Ma得a=,可见图象的斜率为小车和砝码的总质量的倒数.
(3)图象与F轴的截距表示加速度恰好为零时的拉力,也即是小车受到的阻力,大小为0.1 N.
(4)由图可知图线斜率k=1(kg-1),由k=可得:M=1 kg.
答案:(1)见解析图 (2)小车和砝码的总质量的倒数
(3)小车受到的阻力为0.1 N (4)1
3.(2010·阳江模拟)为了探究加速度与力的关系,使用如图实-4-8所示的气垫导轨装置进行实验.其中G1、G2为两个光电门,它们与数字计时器相连,当滑行器通过G1、G2光电门时,光束被遮挡的时间Δt1、Δt2都可以被测量并记录,滑行器连同上面固定的一条形挡光片的总质量为M,挡光片宽度为D,光电门间距离为x,牵引砝码的质量为m.回答下列问题:
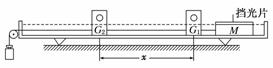
图实-4-8
(1)实验开始应先调节气垫导轨下面的螺钉,使气垫导轨水平,在不增加其他仪器的情况下,如何判定调节是否到位?
答:____________________________________________________________________.
(2)若取M=0.4 kg,改变m的值,进行多次实验,以下m的取值不合适的一个是
__________.
A.m1=5 g B.m2=15 g
C.m3=40 g D.m4=400 g
(3)在此实验中,需要测得每一个牵引力对应的加速度,求得的加速度的表达式为
____________________________________________________________________.
(用Δt1、Δt2、D、x表示)
解析:(1)如果气垫导轨水平,则不挂砝码时,M应能在任意位置静止不动,或推动M后能使M匀速运动.
(2)应满足M≫m,故m4=400 g不合适.
(3)由v1=,v2=,v22-v12=2ax
可得:a=.
答案:(1)取下牵引砝码,M放在任意位置都不动;或取下牵引砝码,轻推滑行器M,数字计时器记录每一个光电门的光束被挡的时间Δt都相等
(2)D
(3)a=
2.(2010·台州模拟)如图实-4-7所示,在探究牛顿运动定律的演示实验中,若1、2两个相同的小车所受拉力分别为F1、F2,车中所放砝码的质量分别为m1、m2,打开夹子后经过相同的时间两车的位移分别为x1、x2,则在实验误差允许的范围内,有( )
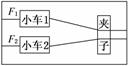
图实-4-7
A.当m1=m2、F1=2F2时,x1=2x2
B.当m1=m2、F1=2F2时,x2=2x1
C.当m1=2m2、F1=F2时,x1=2x2
D.当m1=2m2、F1=F2时,x2=2x1
解析:当m1=m2、F1=2F2时,由F=ma可知,a1=2a2,再由x=at2可得:x1=2x2,故A正确,B错误;当m1=2m2、F1=F2时,a1=a2,再由x=at2可得:x1=x2,故C错误,D正确.
答案:AD
1.关于“验证牛顿运动定律”的实验,下列说法中符合实际的是 ( )
A.通过同时改变小车的质量m及受到的拉力F的研究,能归纳出加速度、力、质量三者之间的关系
B.通过保持小车质量不变,只改变小车的拉力的研究,就可以归纳出加速度、力、质量三者之间的关系
C.通过保持小车受力不变,只改变小车质量的研究,就可以得出加速度、力、质量三者之间的关系
D.先不改变小车质量,研究加速度与力的关系;再不改变受力,研究加速度与质量的关系,最后归纳出加速度、力、质量三者之间的关系
解析:验证牛顿运动定律的实验,是利用控制变量法,探究加速度a与合外力F、物体质量m的关系,故D项正确.
答案:D
12.(16分)如图9所示,在距地面80 m高的水平面上做匀加速直线运动的飞机上每隔
1 s依次放下M、N、P三物体,抛出点a、b与b、c间距分别为45 m和55 m,分
别落在水平地面上的A、B、C处.求:
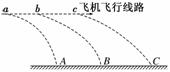
图9
(1)飞机飞行的加速度;
(2)刚放下N物体时飞机的速度大小;
(3)N、P两物体落地点B、C间的距离.
解析:(1)飞机在水平方向上,由a经b到c做匀加速直线运动,由Δx=a0T2得,
a0===10 m/s2.
(2)因位置b对应a到c过程的中间时刻,故有
vb==50 m/s.
(3)设物体落地时间为t,
由h=gt2得:t= =4 s
BC间的距离为:BC=bc+vct-vbt
又vc-vb=a0T
得:BC=bc+a0Tt=95 m.
答案:(1)10 m/s2 (2)50 m/s (3)95 m
11.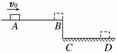 (14分)(2010·泰安模拟)如图8所示,水平台AB距地面CD
(14分)(2010·泰安模拟)如图8所示,水平台AB距地面CD
高h=0.8 m.有一滑块从A点以6.0 m/s的初速度在平台上
做匀变速直线运动,并从平台边缘的B点水平飞出,最后落
在地面上的D点.已知AB=2.20 m,落地点到平台的水平 图8
距离为2.00 m.(不计空气阻力,g取10 m/s2)求滑块从A到D所用的时间和滑块与
平台间的动摩擦因数.
解析:设滑块从A到B所用时间为t1,位移为x1,加速度为a,从B点飞出时的速
度为vB,从B点到落地点的水平位移为x2,飞行时间为t2.
滑块在AB间做匀减速直线运动
vB=v0-at1 ①
vB2=v02-2ax1 ②
根据牛顿第二定律列出:μmg=ma ③
滑块在BD间做平抛运动,h=gt22 ④
x2=vBt2 ⑤
从A到D所用的时间t=t1+t2 ⑥
根据①②③④⑤⑥各式求得:t=0.8 s,μ=0.25.
答案:0.8 s 0.25
10.(2010·惠州模拟)从某一高度以相同速度相隔1 s先后水平抛出甲、乙两个小球,不
计空气阻力,在乙球抛出后两球在空气中运动的过程中,下述说法正确的是 ( )
A.两球水平方向的距离越来越大
B.两球竖直高度差越来越大
C.两球水平方向的速度差越来越大
D.两球每秒内的速度变化量相同,与其质重无关
解析:水平方向上两小球距离Δx=v0(t1-t2)=v0,Δvx=0恒定;竖直方向上两小球
距离Δy=gt12-gt22=g(t2+1)2-gt22=gt2+g变大,Δvy=gt1-gt2=g(t2+1)-gt2
=g恒定,每秒速度变化量即加速度(重力加速度)大小和方向均相同,与质量无关,
故B、D正确.
答案:BD
9.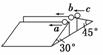 如图7所示,两个倾角分别为30°、45°的光滑斜面放在同一水
如图7所示,两个倾角分别为30°、45°的光滑斜面放在同一水
平面上,两斜面间距大于小球直径,斜面高度相等.有三个完全
相同的小球a、b、c,开始均静止于同一高度处,其中b小球在
两斜面之间,a、c两小球在斜面顶端.若同时释放,小球a、b、 图7
c到达该水平面的时间分别为t1、t2、t3.若同时沿水平方向抛出,初速度方向如图7
所示,小球a、b、c到达该水平面的时间分别为t1′、t2′、t3′.下列关于时间的关
系正确的是 ( )
A.t1>t3>t2 B.t1=t1′、t2=t2′、t3=t3′
C. t1′>t2′>t3′ D.t1<t1′、t2<t2′、t3<t3′
解析:设三小球在高为h的同一高度处.由静止释放三小球时
对a:=gsin30°·t12,则t12=.
对b:h=gt22,则t22=.
对c:=gsin45°·t32,则t32=.
所以t1>t3>t2.
当平抛三小球时:小球b做平抛运动,竖直方向运动情况同第一种情况;小球a、c
在斜面内做类平抛运动,沿斜面向下方向的运动同第一种情况,所以t1=t1′、t2=
t2′、t3=t3′.故选A、B.
答案:AB
8.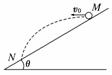 (2010·温州模拟)如图6所示,从倾角为θ的斜面上的M点
(2010·温州模拟)如图6所示,从倾角为θ的斜面上的M点
水平抛出一个小球,小球的初速度为v0,最后小球落在斜面
上的N点,则(重力加速度为g) ( )
A.可求M、N之间的距离
B.不能求出小球落到N点时速度的大小和方向 图6
C.可求小球到达N点时的动能
D.可以断定,当小球速度方向与斜面平行时,小球与斜面间的距离最大
解析:设小球从抛出到落到N点经历时间为t,则有tanθ==,t=,
因此可求出dMN==,vN=,方向(与水平方向的夹角):tanα
=,故A正确、B错误.但因小球的质量未知,因此小球在N点时的动能不能求
出,C错误.当小球的速度方向与斜面平行时,小球垂直于斜面方向的速度为零,
此时小球与斜面间的距离最大,D正确.
答案:AD
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com