
题目列表(包括答案和解析)
3.如图所示,在粗糙斜面顶端固定轻弹簧的一端,另一端挂一物体,物体在A点处于平衡状态.现用平行于斜面向下的力拉物体,第一次直接拉到B点,第二次将物体先拉到C点,再回到B点,在这两次过程中下列说法正确的是 ( )
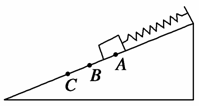
A.重力势能的改变量相等
B.弹性势能的改变量相等
C.摩擦力对物体做的功相等
D.弹簧弹力对物体做的功相等
[答案] ABD
[解析] 两次过程初末位置相同,所以重力和弹簧的弹力做的功是相同的,此题中滑动摩擦力始终做负功,大小为摩擦力与物体在摩擦力作用下运动的路程的乘积,所以两次做功不同.
2.(2009·大连模拟)如图所示,在高1.5m的光滑平台上有一个质量为2kg的小球被一细线拴在墙上,球与墙之间有一根被压缩的轻质弹簧.当烧断细线时,小球被弹出,小球落地时的速度方向与水平方向成60°角,则弹簧被压缩时具有的弹性势能为(g=10m/s2) ( )
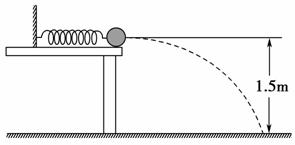
A.10J B.15J
C.20J D.25J
[答案] A
[解析] 由h=gt2和vy=gt得:vy=m/s,落地时,tan60°=可得:v0==m/s,由机械能守恒得:Ep=mv,可求得:Ep=10J,故A正确.
1.跳伞运动员在刚跳离飞机、降落伞尚未打开的一段时间内:①空气阻力做正功;②重力势能增加;③动能增加;④空气阻力做负功.以下说法中正确的是 ( )
A.①② B.③④
C.②④ D.①③
[答案] B
[解析] 跳伞运动员跳离飞机,在尚未打开降落伞的这段时间内,运动员向下运动,重力对运动员做正功,重力势能减少;空气阻力对运动员做负功.由于重力大于空气阻力,运动员向下做加速运动,其动能增加,故①②错,③④对.
14.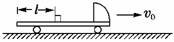 如图所示,一平板车以某一速度v0匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为l=3m,货箱放入车上的同时,平板车开始刹车,刹车过程可视为做a=4m/s2的匀减速直线运动.已知货箱与平板车之间的动摩擦因数为μ=0.2,g=10m/s2.为使货箱不从平板车上掉下来,平板车匀速行驶的速度v0应满足什么条件?
如图所示,一平板车以某一速度v0匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为l=3m,货箱放入车上的同时,平板车开始刹车,刹车过程可视为做a=4m/s2的匀减速直线运动.已知货箱与平板车之间的动摩擦因数为μ=0.2,g=10m/s2.为使货箱不从平板车上掉下来,平板车匀速行驶的速度v0应满足什么条件?
[答案] v0≤6m/s
[解析] 设经过时间t,货箱和平板车达到共同速度v,以货箱为研究对象,由牛顿第二定律得,货箱向右做匀加速运动的加速度a1=μg.
货箱向右运动的位移x箱=a1t2,
又v=a1t
平板车向右运动的位移x车=v0t-at2
又v=v0-at
为使货箱不从平板车上掉下来,应满足:x车-x箱≤l
联立得:v0≤
代入数据:v0≤6m/s.
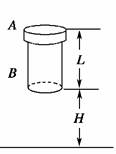
13.如图所示,一个厚度不计的圆环A,紧套在长度为L的圆柱体B的上端,A、B两者的质量均为m,A与B之间的最大静摩擦力与滑动摩擦力相同,其大小为kmg(k>1).B在离地H高处由静止开始落下,触地后能竖直向上弹起,触地时间极短,且无动能损失,B与地碰撞若干次后A与B分离.求:
(1)B与地第一次碰撞后,经多长时间A与B达到相同的速度;
(2)当A与B第一次达到相同速度时,B下端离地面的高度是多少.
[答案] (1) (2)H
[解析] (1)B与地第一次碰撞后,以v0=向上运动,加速度aB=(k+1)g,方向向下;
此时刻A以速度v0=向下运动,加速度aA=(k-1)g,方向向上.
取向下为正方向,设A、B共同速度为v1,
对A有:v1=v0-(k-1)gt,
对B有:v1=-v0+(k+1)gt
解得t=
(2)由以上各式解得,A与B第一次达到的相同速度v1=,方向向下.
解法一 B下端离地面的高度h=v0t-=H.
解法二 用平均速度求解:h=t=H.
解法三 用动能定理:对B,-(mg+kmg)h=mv-mv,解得h=H.
12.跳伞运动员做低空跳伞表演,当飞机在离地面224m高处水平飞行时,运动员离开飞机在竖直方向做自由落体运动,运动一段时间后,立即打开降落伞,展伞后运动员以12.5m/s2的平均加速度匀减速下降,为了运动员的安全,要求运动员落地速度最大不得超过5m/s.g=10m/s2,求:
(1)运动员展伞时离地的高度至少为多少?着地时相当于从多高处自由落下?
(2)运动员在空中的最短时间为多少?
[答案] (1)99m,1.25m (2)8.6s
[解析] 设展伞时跳伞员的速度为v0.距地面的高度为h,到达地面速度为v地.据题意得:
224m-h= ①
v-v=-2ah ②
联立①②得:h=99m,v0=50m/s.
设实际相当于h′高度跳下
则2gh′=v ③
解h′=1.25m
当跳伞员恰好以5m/s的速度落地时间最短,设时间为t,自由下落时间为t1,减速运动时间为t2,据题意:
t=t1+t2 ④
v0=gt1 ⑤
t2=h ⑥
联立第(1)问和④⑤⑥式得
 t=8.6s.
t=8.6s.
0.8v)2=2as′, ②
由s=25m,解得s′=16m. ③
(2)设乙应在距离甲s0处起跑,由几何关系得
s′+s0=vt. ④
s′=t=0.4vt, ⑤
由③④⑤得s0=24m. ⑥
11. 甲、乙两个同学在直跑道上进行4×100m接力(如图所示),他们在奔跑时有相同的最大速度,乙从静止开始全力奔跑需跑出25m才能达到最大速度,这一过程可看作匀加速直线运动.现在甲持棒以最大速度向乙奔来,乙在接力区伺机全力奔出.若要求乙接棒时奔跑的速度达到最大速度的80%,则:
甲、乙两个同学在直跑道上进行4×100m接力(如图所示),他们在奔跑时有相同的最大速度,乙从静止开始全力奔跑需跑出25m才能达到最大速度,这一过程可看作匀加速直线运动.现在甲持棒以最大速度向乙奔来,乙在接力区伺机全力奔出.若要求乙接棒时奔跑的速度达到最大速度的80%,则:
(1)乙在接力区须奔出多少距离?
(2)乙应在距离甲多远时起跑?
[答案] (1)16m (2)24m
[解析] 对于此类问题,关键在于正确分析两物体的运动性质以及物体的运动时间、位移和速度的关系.
(1)乙在接力区做初速度为零的匀加速运动.设乙的加速度为a,速度为0.8v时位移为s′,v2=2as, ①
10.在北京奥运会上,一跳水运动员从离水面10m高的平台上向上跃起,举双臂直体离开台面,此时重心位于从手到脚全长的中点,跃起后重心升高0.45m达到最高点,落水时身体竖直,手先入水,从离开平台到手接触水面,运动员可以用于完成动作的时间为________s,在此过程中,运动员水平方向的运动忽略不计,运动员可视作全部质量集中在重心的一个质点,取g=10m/s2
[答案] 1.7s
[解析] 如图所示,从平台跃起,到手接触水面,运动员重心的高度变化为h=10m
解法一 将整个过程分上升和下降两个阶段考虑,设运动员跃起的初速度为v0,则=H
v0===3(m/s)
故上升时间为:t1==0.3(s)
设运动员从最高点到手接触水面所用时间为t2,则:gt=h+H
t2===1.4(s)
故用于完成动作的时间t为
t=t1+t2=1.7(s)
综上所述,本题正确的答案为1.7s
解法二 运动员的整个运动过程为竖直上抛运动,设总时间为t,由于运动员入水时位于跃起位置下方10m处,故该过程中位移为x=-h,即:
x=v0t-gt2=-h
其中v0=3m/s
代入数据得:5t2-t-10=0
t==1.7(s)(另一根舍去)
9.利用水滴下落可以测量重力加速度g,调节水龙头,让水一滴一滴地流出,在水龙头的正下方放一盘子,调整盘子的高度,使一滴水滴碰到盘子时,恰好有另一滴水从水龙头开始下落,而空中还有两个正在下落的水滴,测出水龙头处到盘子的高度为h(m),再用秒表测量时间,从第一滴水离开水龙头开始,到第N滴水落至盘中,共用时间为T(s),当第一滴水落到盘子时,第二滴水离盘子的高度为________m,重力加速度g=________m/s2.
[答案] h 2(N+2)2h/9T2
[解析] 因为任意两滴水之间的时间间隔相等,设任意两滴水之间的时间间隔为t,第一滴水下落的时间为3t,则有
h=g(3t)2
第一滴水落到盘子时,第二滴水下落的时间为2t
则第二滴水离盘子的高度为
h′=h-g(2t)2=h-h=h
又(N+2)t=T
 故g==2(N+2)2h/9T2
故g==2(N+2)2h/9T2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com