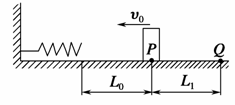
10．一轻弹簧的左端固定在墙壁上，右端自由，一质量为m的滑块从距弹簧右端L₀的P点以初速度v0正对弹簧运动，如下图所示，滑块与水平面的动摩擦因数为μ，在与弹簧碰后反弹回来，最终停在距P点为L₁的Q点，求：在滑块与弹簧碰撞过程中弹簧最大压缩量为多少？

[答案]　－－L₀

[解析]　设弹簧最大压缩量为x，在滑块向左运动的过程中，由动能定理可得：

－μmg(x+L₀)－W_弹＝0－mv20　　　　　　　　　　　 ①

在滑块返回的过程中，由动能定理得：

W_弹－μmg(x+L₀+L₁)＝0　　　　　　　　　　　　　　　　 ②

由①②得：x＝－－L₀

整个过程弹簧对滑块作功为零，本题也可全过程列方程求解．

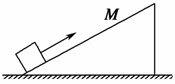
9．如图所示，物体以100J的初动能从斜面的底端向上运动，当它通过斜面上的M点时，其动能减少80J，机械能减少32J.如果物体能从斜面上返回底端，则物体到达底端时的动能为________．

[答案]　20J

[解析]　因物体从斜面底端到达M点的过程中机械能减少32J，即摩擦生热32J，在斜面上物体受的各个力的大小不变，所以从M点到最高点，动能减少20J，摩擦生热8J，所以上滑过程摩擦生热40J，物体返回斜面底端时机械能损失也等于40J，此时动能应为100J－80J＝20J.

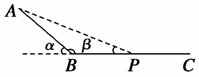
8．(2009·如皋模拟)如图所示，斜面AB和水平面BC是由同一板材上截下的两段，在B处用小圆弧连接．将小铁块(可视为质点)从A处由静止释放后，它沿斜面向下滑行，进入平面，最终静止于P处．若从该板材上再截下一段，搁置在A、P之间，构成一个新的斜面，再将铁块放回A处，并轻推一下使之沿新斜面向下滑动．关于此情况下铁块运动情况的描述，正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．铁块一定能够到达P点

B．铁块的初速度必须足够大才能到达P点

C．铁块能否到达P点与铁块质量有关

D．铁块能否到达P点与铁块质量无关

[答案]　AD

[解析]　设AB＝x₁，BP＝x₂，AP＝x₃，动摩擦因数为μ，由动能定理得：mgx₁sinα－μmgcosαx₁－μmgx₂＝0，可得：mgx₁sinα＝μmg(x₁cosα+x₂)，设沿AP滑到P的速度为v_P，由动能定理得：mgx₁sinα－μmgcosβ·x₃＝mv，因x₁cosα+x₂＝x₃cosβ，故得：v_P＝0，也即铁块恰好沿AP滑到P点与铁块质量无关，故A、D正确．

7．一辆汽车在平直的公路上以速度v₀开始加速行驶，经过一段时间t，前进了距离s，此时恰好达到其最大速度v_m.设此过程中汽车发动机始终以额定功率P工作，汽车所受的阻力恒为F，则在这段时间里，发动机所做的功为　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

A．Fv_mt　 　　　　　　　　　　　　　　　　　　　　　　　 B．Pt

C.mv+Fs－mv　 　　　　　　　　　　　　　　　 D．Ft

[答案]　ABC

[解析]　发动机恒功率，故W＝Pt，B正确；

又因为汽车速度达到v_m时阻力与牵引力相等，则P＝Fv_m，所以W＝Fv_mt，A正确；

又由动能定理知Pt－Fs＝mv－mv

得Pt＝Fs+mv－mv，C正确；

因为这一过程不是匀变速直线运动，平均速度不等于，位移也不等于t，发动机所做的功也不等于阻力做的功，所以D错．

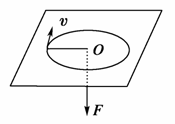
6．如右图所示，质量为m的物体用细绳经过光滑小孔牵引在光滑水平面上做匀速圆周运动，拉力为某个值F时，转动半径为R，当拉力逐渐减小到时，物体仍做匀速圆周运动，半径为2R，则外力对物体所做的功大小是　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．0

[答案]　A

[解析]　设当绳的拉力为F时，小球做匀速圆周运动时线速度为v₁，则有

F＝m.

当绳的拉力减为时，小球做匀速圆周运动的线速度为v₂，则有

F＝m.

在绳的拉力由F减为F的过程中，绳的拉力所做的功为

W＝mv－mv＝－FR.

所以，绳的拉力所做功的大小为FR.

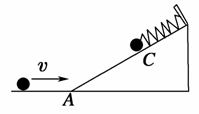
5．如图所示，光滑斜面的顶端固定一弹簧，一物体向右滑行，并冲上固定在地面上的斜面．设物体在斜面最低点A的速度为v，压缩弹簧至C点时弹簧最短，C点距地面高度为h，则从A到C的过程中弹簧弹力做功是　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

A．mgh－mv²　 　　　　　　　　　　　　　　　　　　 B.mv²－mgh

C．－mgh　 　　　　　　　　　　　　　　　　　　　　　　 D．－(mgh+mv²)

[答案]　A

[解析]　由A到C的过程运用动能定理可得：

－mgh+W＝0－mv²

所以W＝mgh－mv²，所以A正确．

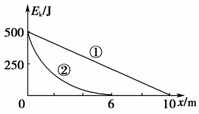
4．构建和谐型、节约型社会深得民心，遍布于生活的方方面面．自动充电式电动车就是很好的一例，电动车的前轮装有发电机，发电机与蓄电池连接．当在骑车者用力蹬车或电动自行车自动滑行时，自行车就可以连通发电机向蓄电池充电，将其他形式的能转化成电能储存起来．现有某人骑车以500J的初动能在粗糙的水平路面上滑行，第一次关闭自充电装置，让车自由滑行，其动能随位移变化关系如图①所示；第二次启动自充电装置，其动能随位移变化关系如图线②所示，则第二次向蓄电池所充的电能是　　　　　　　　　　　　　　　　　 (　)

A．200J　 　　　　　　　　　　　　　　　　　　　　　　　 B．250J

C．300J　 　　　　　　　　　　　　　　　　　　　　　　　 D．500J

[答案]　A

[解析]　设自行车与路面的摩擦阻力为F_f，由图可知，关闭自动充电装置时，由动能定理得：0－E_k0＝－F_f·x₁，可得F_f＝50N，启动自充电装置后，自行车向前滑行时用于克服摩擦做功为：W＝F_fx₂＝300J，设克服电磁阻力做功为W′，由动能定理得：－W′－W＝0－E_k0，可得W′＝200J，故A正确．

3．在2009年10月全运会上，跳水运动员从10米高处的跳台跳下，设水的平均阻力均为运动员体重的3倍，在粗略估算中，把运动员当作质点处理，为了保证运动员的人身安全，池水深度至少为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　 (　)

A．5m　 　　　　　　　 　　　　　　　　　　　　　　　　　 B．3m

C．7m　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．1m

[答案]　A

[解析]　对运动员跳水的全过程研究

据动能定理有：

mg(H+h)－fh＝ΔE_k＝0

其中m为运动员质量，h为运动员入水的深度

又H＝10m，f＝3mg

∴h＝＝5m

为保证人身安全，池水深度H ′≥h

即H′≥5m

∴水深至少5m，A选项正确．

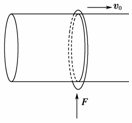
2．如图所示，一个质量为m的圆环套在一根固定的水平长直杆上，环与杆的动摩擦因数为μ.现给环一个向右的初速度v₀，同时对环施加一个竖直向上的作用力F，并使F的大小随环的速度的大小变化，两者关系为F＝kv，其中k为常数，则环在运动过程中克服摩擦所做的功的大小不可能为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　

B．0

C.+　 　　　

D.－

[答案]　C

[解析]　可能圆环最终静止，则－W_f＝0－，W_f＝，A对；可能圆环刚开始运动时，mg＝F＝kv₀，圆环一直做匀速运动，克服摩擦所做的功为零，B对；可能圆环最终做匀速运动，mg＝F＝kv，v＝，则－W_f＝－，化简得W_f＝－，D对，C不可能．

1．在2009年10月全运会田径比赛上，设某运动员臂长为L，将质量为m的铅球推出，铅球出手的速度大小为v₀，方向与水平方向成30°角，则该运动员对铅球所做的功是(　)

A.　　　　　　　　　　　　　　 B．mgL+mv

C.mv　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．mgL+mv.

[答案]　A

[解析]　设运动员对铅球做功为W，由动能定理W－mgLsin30°＝mv，所以W＝mgL+mv.