3．在磁场中的同一位置，先后引入长度相等的直导线a和b，a、b导线的方向均与磁场方向垂直，但两导线中的电流不同，因此所受的力也不一样．下列几幅图象表现的是导线所受的安培力F与通过导线的电流I的关系．a、b各自有一组F、I的数据，在图象中各描出一个点．在下图中，请判断描绘正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

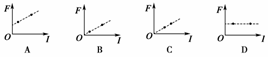
[答案]　BC

[解析]　由题意“同一位置同一磁场”，“导线长度相同”可知斜率相等；电流为零时不受力，所以A、D选项错误．

2．(2010·海门测试)下列四幅图中涉及经典的物理实验研究，其中说法正确的是(　)

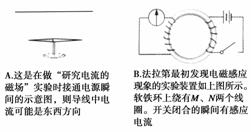
[答案]　BCD

[解析]　通电导线的周围有磁场，处在磁场中的小磁针要受到磁场力作用，若A图中导线有电流，小磁针要发生偏转，图景与实际不符，A项错误；B图中开关闭合，线圈中磁通量变化，产生感应电流，导致电流表的指针偏转；C图中电子在磁场中受到磁场力作用，用左手定则判断电子束将向下偏转；D图中汽车速度达到第一宇宙速度时，汽车环绕地球近地做圆周运动，处在车内的物体处于完全失重状态．

1．在磁场中某区域的磁感线，如图所示，则　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

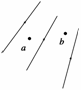A．a、b两处的磁感应强度的大小不等B_a>B_b

B．a、b两处的磁感应强度的大小不等，B_a<B_b

C．同一通电导线放在a处受力一定比放在b处受力大

D．同一通电导线放在a处受力一定比放在b处受力小

[答案]　B

[解析]　磁感线的疏密程度表示B的大小，但安培力的大小 除跟该处的B的大小和I、L有关外，还跟导线放置的方向与B的方向的夹角有关，故C、D错误；由a、b两处磁感线的疏密程度可判断出B_b>B_a，所以B正确．

13．如图所示，在空间有一坐标系xOy，其第一象限内充满着两个匀强磁场区域Ⅰ和Ⅱ，直线OP是它们的边界．区域Ⅰ中的磁感应强度为B，方向垂直于纸面向外；区域Ⅱ中的磁感应强度为2B，方向垂直于纸面向内，边界上的P点坐标为(4L,3L)．一质量为m、电荷量为q的带正电粒子从P点平行于y轴负方向射入区域Ⅰ，经过一段时间后，粒子恰好经过原点O.忽略粒子重力，已知sin37°＝0.6，cos37°＝0.8，求：

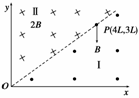
(1)粒子从P点运动到O点的时间至少为多少？

(2)粒子的速度大小可能是多少？

[答案]　(1)　(2)(n＝1,2,3，…)

[解析]　(1)设粒子的入射速度为v，用R₁、R₂、T₁、T₂分别表示粒子在磁场Ⅰ区和Ⅱ区中运动的轨道半径和周期，则有

qvB＝m，qv·2B＝，

T₁＝＝，T₂＝＝.

粒子先在磁场Ⅰ区中做顺时针的圆周运动，后在磁场Ⅱ区中做逆时针的圆周运动，然后从O点射出，这样粒子从P点运动到O点所用的时间最短．

粒子运动轨迹如图所示

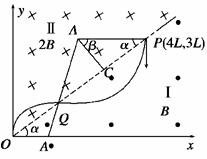
tanα＝＝0.75，

得α＝37°，α+β＝90°.

粒子在磁场Ⅰ区和Ⅱ区中的运动时间分别为

t₁＝·T₁，t₂＝·T₂，

粒子从P点运动到O点的时间至少为t＝t₁+t₂，

由以上各式解得t＝.

(2)当粒子的速度大小满足一定条件时，粒子先在磁场Ⅰ区中运动，后在磁场Ⅱ区中运动，然后又重复前面的运动，直到经过原点O.这样粒子经过n个周期性的运动到达O点，每个周期的运动情况相同，粒子在一个周期内的位移为

s＝＝＝(n＝1,2,3，…)．

粒子每次在磁场Ⅰ区中运动的位移为s₁＝s＝s，

由图中的几何关系可知　＝cosα，

由以上各式解得粒子的速度大小为

v＝(n＝1,2,3，…)．

12．(2010·天津市高三十校联考)如图所示，在空间中固定放置一绝缘材料制成的边长为L的刚性等边三角形框架△DEF，DE边上S点处有一发射带正电的粒子源，发射粒子的方向皆在图中截面内且垂直于DE边向下．发射的电荷量皆为q，质量皆为m，但速度v有各种不同的值．整个空间充满磁感应强度大小为B，方向垂直截面向里的均匀磁场．设粒子与△DEF边框碰撞时没有能量损失和电荷量传递．求：

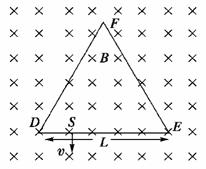
(1)带电粒子速度的大小为v时，做匀速圆周运动的半径；

(2)带电粒子速度v的大小满足什么条件时，可使S点发出的粒子最终又垂直于DE边回到S点？

(3)这些粒子中，回到S点所用的最短时间是多少？

[答案]　(1)　(2)　(n＝0,1,2,3，…)　(3)

[解析]　(1)带电粒子从S点垂直于DE边以速度v射出后，做匀速圆周运动，其圆心一定位于DE边上，其半径R可由qvB＝求得，R＝①

(2)要求此粒子每次与△DEF的三条边碰撞时都与边垂直，且能回到S点，则R和v应满足以下条件：

＝＝(2n－1)R　(n＝1,2,3，…)②

由①②得v＝　(n＝1,2,3，…)③

(3)这些粒子在磁场中做圆周运动的周期为

T＝将①式代入，得T＝④

可见在B及给定时T与v无关．粒子从S点出发最后回到S点的过程中，与△DEF的边碰撞次数越少，所经历的时间就越短，所以应取n＝1，由图可看出该粒子的轨迹包括3个半圆和3个圆心角为300°的圆弧，故最短时间为

t＝3×+3×＝4T＝⑤

11．一匀强磁场，磁场方向垂直于xOy平面．在xOy平面上，磁场分布在以O为圆心的一个圆形区域内．一个质量为m、电荷量为q的带电粒子，由原点O开始运动，初速度为v，方向沿x轴正方向．后来，粒子经过y轴上的P点，此时速度方向与y轴的夹角为30°，P点到O点的距离为L，如图所示．不计重力的影响，求磁场的磁感应强度B的大小和xOy平面上磁场区域的半径R.

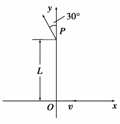
[答案]　L

[解析]　粒子在磁场中受洛伦兹力作用，做匀速圆周运动，设其半径为r，　qvB＝m①

据此并由题意知，粒子在磁场中的轨迹的圆心C必在y轴上，且P点在磁场区域之外．过P沿速度方向作反向延长线，它与x轴相交于Q点．作圆弧过O点与x轴相切，并且与PQ相切，切点A即粒子离开磁场区域的点．这样可得到圆弧轨迹的圆心C，如图所示．

由图中几何关系得L＝3r.②

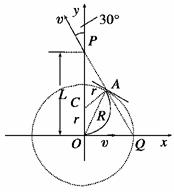
由①②求得，B＝.③

图中OA即为圆形磁场区域的半径R，由几何关系得R＝L.

10．如图所示，直线MN上方有磁感应强度为B的匀强磁场．正、负电子同时从同一点O以与MN成30°角的同样速度v射入磁场(电子质量为m，电荷为e)，它们从磁场中射出时相距多远？射出的时间差是多少？

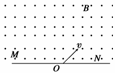
[答案]　

[解析]　由公式轨道半径R＝和周期T＝知，它们的半径和周期是相同的．只是偏转方向相反．先确定圆心，画轨迹，后由几何关系求半径，由对称性知：射入、射出点和圆心恰好组成正三角形．所以两个射出点相距2R＝.

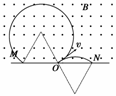
由图还可看出，经历时间相差＝.

9．如图MN表示垂直纸面的平板，它的一侧有匀强磁场，磁场方向垂直纸面向里，磁感应强度大小为B.一带电粒子从平板上的狭缝O处以垂直于平板的初速度v射入磁场区域，最后到达平板上的P点．已知B、v以及P到O的距离l.不计重力，则此粒子的比荷为________．

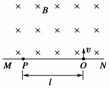
[答案]　

[解析]　因粒子经O点时的速度垂直于OP，故OP＝2R，

又R＝，所以＝.

8．(2010·吉林市统考)摆线是数学中众多迷人曲线之一，它是这样定义的：一个圆沿一直线无滑动地滚动，则圆上一固定点所经过的轨迹称为摆线．在竖直平面内有xOy坐标系，空间存在垂直xOy平面向里的匀强磁场，磁感应强度为B，一质量为m，电荷量为+q的小球从坐标原点由静止释放，小球的轨迹就是摆线．小球在O点速度为0时，可以分解为一水平向右的速度v₀和一水平向左的速度v₀两个分速度，如果v₀取适当的值，就可以把摆线分解成以v₀的速度向右做匀速直线运动和从O点向左速度为v₀的匀速圆周运动两个分运动．设重力加速度为g，下列式子正确的是　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　 (　)

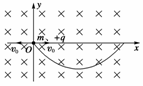
A．速度v₀所取的适当值应为

B．经过t＝第一次到达摆线最低点

C．最低点的y轴坐标为y＝－

D．最低点的y轴坐标为y＝－

[答案]　ABC

[解析]　以匀速直线运动分析，应有mg＝qv₀B，则速度v₀所取的适当值应为v₀＝，选项A正确；以匀速圆周运动分析，经过周期到达最低点，则t＝＝，经过t＝第一次到达摆线最低点，选项B正确；最低点的y轴坐标为y＝－2R＝－＝－，选项C正确；选项D错误．

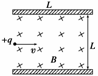
7．如图所示，长为L的水平极板间有垂直于纸面向内的匀强磁场，磁感应强度为B，板间距离也为L，板不带电．现有质量为m、电荷量为q的带正电粒子(不计重力)，从左边极板间中点处垂直磁感线以速度v水平射入磁场，欲使粒子不打在极板上，可采用的办法是

(　)

A．使粒子的速度v<

B．使粒子的速度v>

C．使粒子的速度v>

D．使粒子的速度<v<

[答案]　AB

[解析]　由左手定则判得粒子在磁场中间向上偏，做匀速圆周运动．很明显，圆周运动的半径大于某值r₁时粒子可以从极板右边穿出，而半径小于某值r₂时粒子可从极板的左边穿出

现在问题归结为求粒子能从右边穿出时r的最小值r₁以及粒子从左边穿出时r的最大值r₂.在图中由几何知识得，粒子擦着板从右边穿出时，圆心在O点，有

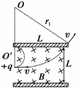
r＝L²+(r₁－)²，得r₁＝.

由于r₁＝，得v₁＝，

所以v>时粒子能从右边穿出．

粒子擦着上板从左边穿出时，圆心在O′点，有r₂＝，

由r₂＝，得v₂＝，

所以v<时粒子能从左边穿出．