14．(10分) 如图16所示，光滑小圆环A吊着一个

重为G₁的砝码套在另一个竖直放置的大圆环上，

今有一细绳拴在小圆环A上，另一端跨过固定在

大圆环最高点B处的一个小滑轮后吊着一个重为

G₂的砝码，如果不计小环、滑轮、绳子的重量大小．　　　　　 图16

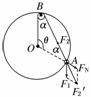绳子又不可伸长，求平衡时弦AB所对的圆心角θ.

解析：以小圆环A为研究对象，它受到的力有：

竖直绳对它的拉力F₁＝G₁，其方向竖直向下；

AB绳对它的拉力F₂=G₂，其方向沿AB方向；

大圆环对它的弹力FN，其方向沿半径指向圆外，

在F₁、F₂、F_N三力的共同作用下，小圆环处于平衡状态．

将小圆环A所受的三个力利用力的合成和力的分解，组成三角形，如图所示．

由几何关系得△OAB与△F_NAF₂′相似，得

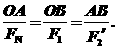
所以F_N＝F₁，sin＝，

将F₁＝G₁、F₂＝G₂代入

解得θ＝2arcsin.

答案：2arcsin

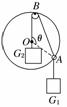
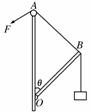
13．(8分) 如图15所示，轻杆BC的C点用

光滑铰链与墙壁固定，杆的B点通过水

平细绳AB使杆与竖直墙壁保持30°的夹角．

若在B点悬挂一个定滑轮(不计重力)，某

人用它匀速地提起重物．已知重物的质量　　　　　　　 图15

m＝30 kg，人的质量M＝50kg，g取10 m/s².试求：

(1)此时地面对人的支持力的大小；

(2)轻杆BC和绳AB所受力的大小．

解析：(1)因匀速提起重物，则F_T＝mg.且绳对人的拉力为mg，所以地面对人的支持力为：F_N＝Mg－mg＝(50－30)×10 N＝200 N，方向竖直向上．

(2)定滑轮对B点的拉力方向竖直向下，大小为2mg，杆对B点的弹力方向沿杆的方向，由共点力平衡条件得：

F_AB＝2mgtan30° ＝2×30×10× N＝200 N

F_BC＝＝ N＝400 N.

答案：(1)200 N　(2)400 N　200 N

12．(5分) (2010·苏南模拟)在“验证力的平行四边

形定则”的实验中，需要将橡皮条的一端固定在

水平木板上，另一端系上两根细绳，细绳的另一

端都有绳套(如图14)．实验中需用两个弹簧测力

计分别勾住绳套，并互成角度地拉橡皮条，使橡　　　　　　　 图14

皮条伸长，结点到达某一位置O.

(1)某同学在做该实验时认为：

A．拉橡皮条的绳细一些且长一些，实验效果较好

B．拉橡皮条时，弹簧测力计、橡皮条、细绳应贴近木板且与木板平面平行

C．橡皮条弹性要好，拉结点到达某一位置O时，拉力要适当大些

D．拉力F₁和F₂的夹角越大越好

其中正确的是________(填入相应的字母)．

(2)若两个弹簧测力计的读数均为4 N，且两弹簧测力计拉力的方向相互垂直，则________(选填“能”或“不能”)用一个量程为5 N的弹簧测力计测量出它们的合力，理由是__________________________．

解析：(1)拉力F₁和F₂的夹角越大，而合力小，作图时相对误差太大，正确的选项为A、B、C.

(2)若两个弹簧测力计的读数均为4 N，且两弹簧测力计拉力的方向相互垂直，则其合力为4 N＞5 N，故不能用一个量程为5 N的弹簧测力计测量出它们的合力．

答案：(1)A、B、C　(2)不能　量程太小

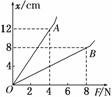
11．(5分)(2010·广州调研)为了探究弹簧弹力F

和弹簧伸长量x的关系，某同学选了A、B两

根规格不同的弹簧进行测试，根据测得的数据

绘出如图13所示的图象，从图象上看，该同

学没能完全按实验要求做，使图象上端成为

曲线，图象上端成为曲线的原因是______________．　　　　 图1

B弹簧的劲度系数为________．若要制作一个精确度较高的弹簧测力计，应选弹簧________(填A或B)．

解析：在弹簧的弹性限度以内，弹力与形变量是成正比的，图象上端出现弯曲是因为拉力过大，超过了弹簧的弹性限度．由胡克定律得x＝，则图线斜率的倒数等于弹簧的劲度系数k＝＝100 N/m.精确度高意味着相同拉力下形变量大，相同刻度线下最小分度值小，故应选用劲度系数小的弹簧A.

答案：拉力过大，超过了弹簧的弹性限度　100 N/m　A

10.(2010·南平模拟)如图12所示，倾角为θ的斜面

体C置于水平面上，B置于斜面上，通过细绳跨

过光滑的定滑轮与A相连接，连接B的一段细绳

与斜面平行，A、B、C都处于静止状态．则　 (　)

A．B受到C的摩擦力一定不为零

B．C受到水平面的摩擦力一定为零

C．水平面对C的支持力与B、C的总重力大小相等

D．若将细绳剪断，B物体依然静止在斜面上，水平面对C的摩擦力为零

解析：若绳对B的拉力恰好与B的重力沿斜面向下的分力相等，则B与C间的摩擦力为零，A项错误；利用整体法判断，C一定受到水平面向左的摩擦力，B项错误；同理在竖直方向利用整体法判断，水平面对C的支持力小于B、C的总重力，C项错误；利用整体法判断BC系统在水平方向不受外力作用，D项正确．

答案：D

9．(2010·苏州模拟) 长直木板的上表面的一端放置

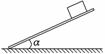一个铁块，木板放置在水平面上，将放置铁块的

一端由水平位置缓慢地向上抬起，木板另一端相

对水平面的位置保持不变，如图10所示．铁块受

到的摩擦力F_f随木板倾角α变化的图线在图11中　　　　　 图10

正确的是(设最大静摩擦力的大小等于滑动摩擦力大小)　　　　　　　　 (　)

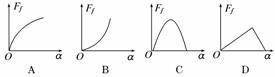
图11

解析：本题应分三种情况进行分析：

(1)当0°≤α＜arctanμ(μ为铁块与木板间的动摩擦因数)时，铁块相对木板处于静止状态，铁块受静摩擦力作用，其大小与重力沿木板(斜面)方向分力大小相等，即F_f＝mgsinα，α＝0°时，F_f＝0；F_f随α的增大按正弦规律增大．

(2)当α＝arctanμ时处于临界状态，此时摩擦力达到最大静摩擦力，由题设条件可知其等于滑动摩擦力大小．

(3)当arctanμ＜α≤90°时，铁块相对木板向下滑动，铁块受到滑动摩擦力的作用，可知F_f＝μF_N＝μmgcosα，F_f随α的增大按余弦规律减小．

答案：C

8.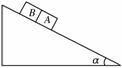 (2008·全国卷Ⅱ)如图9所示，一固定斜面

上两个质量相同的小物块A和B紧挨着匀

速下滑，A与B的接触面光滑．已知A与

斜面之间的动摩擦因数是B与斜面之间动　　　　　　　 图9

摩擦因数的2倍，斜面倾角为α，B与斜面之间的动摩擦因数是　 　　　　(　)

A.tanα　　　　　　　　 B.cotα

C．tanα　　　　　　　 D．cotα

解析：A、B两物体受到斜面的支持力均为mgcosα，所受滑动摩擦力分别为：F_fA＝μ_Amgcosα，F_fB＝μ_Bmgcosα，对整体受力分析结合平衡条件可得：2mgsinα＝μ_Amgcosα+μ_Bmgcosα，且μ_A＝2μ_B，解之得μ_B＝tanα，A项正确．

答案：A

7．(2010·济宁模拟) A、B、C三个物体通过细线

和光滑的滑轮相连，处于静止状态，如图7

所示，C是一箱砂子，砂子和箱的重力都等于

G，动滑轮的质量不计，打开箱子下端开口，

使砂子均匀流出，经过时间t₀流完，则如图8

所示的哪个图线表示在这个过程中桌面对物体　　　　　　　 图7

B的摩擦力F_f随时间的变化关系　　　　　　　　　　　　　　　　　　 (　)

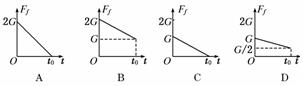
图8

解析：选择A、B整体作为研究对象，由于这个整体开始处于静止状态，所以后来应该一直处于静止状态，整体共受到5个力的作用，即：重力G＝G_A+G_B、支持力F_N、静摩擦力F_f、两根绳子的拉力F₁和F₂.其中F₁＝F₂＝.根据平衡条件得：F_f＝F₁+F₂＝G_C.所以当砂子均匀流出时，B选项正确．

答案：B

6．一轻杆BO，其O端用光滑铰链铰于固定

竖直杆AO上，B端挂一重物，且系一细

绳，细绳跨过杆顶A处的光滑小滑轮，用

力F拉住，如图6所示．现将细绳缓慢往

左拉，使杆BO与杆AO间的夹角θ逐渐减　　　　　　 图6

小，则在此过程中，拉力F及杆BO所受压力F_N的大小变化情况是　　　 (　)

A．F_N先减小，后增大

B．F_N始终不变

C．F先减小，后增大

D．F逐渐减小

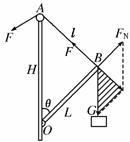解析：取BO杆的B端为研究对象，受到绳子

拉力(大小为F)、BO杆的支持力FN　　　　

和悬挂重物的绳子的拉力(大小为G)的作用，

将FN与G合成，其合力与F等值反　

向，如图所示，得到一个力三角形(如图中画斜线

部分)，此力三角形与几何三角形OBA

相似，可利用相似三角形对应边成比例来解．

如图所示，力三角形与几何三角形OBA相似，设AO高为H，BO长为L，绳长AB为l，则由对应边成比例可得：

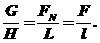，式中G、H、L均不变，l逐渐变小，所以可知FN不变，F逐渐变小．

答案：BD

5. (2009·北京高考)如图5所示，将质量为m的

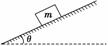滑块放在倾角为θ的固定斜面上．滑块与斜面

之间的动摩擦因数为μ.若滑块与斜面之间的最

大静摩擦力和滑动摩擦力大小相等，重力加速　　　　　　 图5

度为g，则　　　　　　　　　　　　 (　)

A．将滑块由静止释放，如果μ＞tanθ，滑块将下滑

B．给滑块沿斜面向下的初速度，如果μ＜tanθ，滑块将减速下滑

C．用平行于斜面向上的力拉滑块向上匀速滑动，如果μ＝tanθ，拉力大小应是2mgsinθ

D．用平行于斜面向下的力拉滑块向下匀速滑动，如果μ＝tanθ，拉力大小应是mgsinθ

　 解析：对放在斜面上的滑块进行受力分析，当mgsinθ＝μmgcosθ，即μ＝tanθ时，滑块受力平衡，若先前静止，则滑块静止；若有向下的初速度，则做匀速运动．A中，μ＞tanθ，滑块静止在斜面上不会下滑；B中，滑块要加速下滑；C中，拉力沿斜面向上，滑动摩擦力向下，则拉力的大小为2mgsinθ；D中，滑块沿斜面向下匀速滑动，不需要外力作用．

答案：C