
题目列表(包括答案和解析)
15.(10分)一质量为m、电荷量为q的带负电的带电粒子,
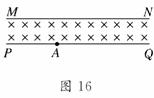
从A点射入宽度为d、磁感应强度为B的匀强磁场,MN、
PQ为该磁场的边界线,磁感线垂直于纸面向里,磁场区
域足够长.如图16所示.带电粒子射入时的初速度与
PQ成45°角,且粒子恰好没有从MN射出.(不计粒子所受重力)求:
(1)该带电粒子的初速度v0;
(2)该带电粒子从PQ边界射出的射出点到A点的距离x.
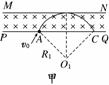
解析:(1)若初速度向右上方,设轨道半径为R1,如图甲所示.
则R1=(R1-d)/cos45°,
R1=(2+)d.
又R1=,解得v0=.
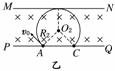
若初速度向左上方,设轨道半径为R2,如图乙所示.
则(d-R2)/cos45°=R2,
R2=(2-)d,v0=.
(2)若初速度向右上方,设射出点C到A点的距离为x1,
则x1=R1=2(+1)d.
若初速度向左上方,设射出点到A点的距离为x2,
则x2=R2=2(-1)d.
答案:见解析
14. (10分)据报道,最近已研制出一种可以投入使用的
(10分)据报道,最近已研制出一种可以投入使用的
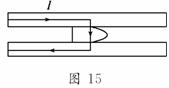
电磁轨道炮,其原理如图15所示.炮弹(可视为长方形
导体)置于两固定的平行导轨之间,并与轨道壁密接.开
始时炮弹在导轨的一端,通电流后,炮弹会被磁场力
加速,最后从位于导轨另一端的出口高速射出.设两导轨之间的距离d=0.10 m,导
轨长 L=5.0 m,炮弹质量m=0.30 kg.导轨上的电流I的方向如图中箭头所示.可认
为,炮弹在轨道内运动时,它所在处磁场的磁感应强度始终为B=2.0 T,方向垂直
于纸面向里.若炮弹出口速度为 v=2.0×103 m/s,求通过导轨的电流I.(忽略摩擦力
与重力的影响)
解析:当导轨通有电流I时,炮弹作为导体受到磁场施加的安培力为
F=IdB ①
设炮弹加速度的大小为a,则有
F=ma ②
炮弹在两导轨间做匀加速运动,因而
v2=2aL ③
联立①②③式得
I=
代入题给数据得I=6.0×105 A.
 答案:6.0×105 A
答案:6.0×105 A
算步骤,有数值计算的要注明单位)
13.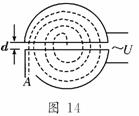 (8分)如图14所示,回旋加速器D形盒的半径为R,
(8分)如图14所示,回旋加速器D形盒的半径为R,
用来加速质量为m、电荷量为q的质子,使质子由静止
加速到能量为E后,由A孔射出,求:
(1)加速器中匀强磁场B的方向和大小;
(2)设两D形盒间距为d,其间电压为U,电场视为匀强
电场,质子每次经电场加速后能量增加,加速到上述能量所需回旋周数;
(3)加速到上述能量所需时间.
解析:(1)带电粒子在磁场中做匀圆周运动,由Bqv=得,v=,又E=mv2
=m()2,
所以B=,方向垂直于纸面向里.
(2)带电粒子每经过一个周期被电场加速二次,能量增加2qU,则:E=2qUn,n=.
(3)可以忽略带电粒子在电场中运动的时间,又带电粒子在磁场中运行周期T=,
所以
t总=nT=×==.
答案:(1) 方向垂直于纸面向里
(2) (3)
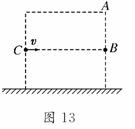
12.带电粒子以速度v沿CB方向射入一横截面为正方形的
区域.C、B均为该正方形两边的中点,如图13所示,不
计粒子的重力.当区域内有竖直方向的匀强电场E时,粒
子从A点飞出,所用时间为t1;当区域内有垂直于纸面向
里的磁感应强度为B的匀强磁场时,粒子也从A点飞出,
所用时间为t2,下列说法正确的是 ( )
A.t1<t2 B.t1>t2
C.=v D.=v
解析:带电粒子在匀强电场中做类平抛运动,水平方向上做匀速运动,而在匀强磁
场中做匀速圆周运动,水平方向上做减速运动,所以t2>t1,A项正确,B项错;设
正方形区域的边长为l,则当加电场时,有l=vt1和=t12,得E=.当加磁场
时,根据几何关系,有(R-)2+l2=R2,得R=l,再由R=得B=.所以=
v,D项对,C项错.
答案:AD
11.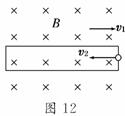 用一金属窄片折成一矩形框架水平放置,框架右边上有一
用一金属窄片折成一矩形框架水平放置,框架右边上有一
极小开口.匀强磁场的磁感应强度大小为B,方向垂直于
纸面向里,如图12所示,框架以速度v1向右匀速运动,
一带电油滴质量为m,电荷量为q,以速度v2从右边开口
处水平向左射入,若油滴恰能在框架内做匀速圆周运动,
则 ( )
A.油滴带正电,且逆时针做匀速圆周运动
B.油滴带负电,且顺时针做匀速圆周运动
C.圆周运动的半径一定等于
D.油滴做圆周运动的周期等于
解析:金属框架在磁场中切割磁感线运动,由右手定则可知上板带正电,下板带负
电.油滴恰能在框架内做匀速圆周运动,说明油滴受的重力与电场力平衡,可判定
油滴带负电.由左手定则可知,油滴沿顺时针方向做匀速圆周运动,A错B对;r=
,C错;设框架宽为l,F=Eq=
q=qBv1=mg,T==·=,D对.
 答案:BD
答案:BD
10.一电子以与磁场垂直的速度v从P处沿PQ方向进入长
为d、宽为h的匀强磁场区域,从N点射出,如图11所示,
若电子质量为m,电荷量为e,磁感应强度为B,则( )
A.h=d
B.电子在磁场中运动的时间为
C.电子在磁场中运动的时间为
D.洛伦兹力对电子做的功为Bevh
解析:过P点和N点作速度的垂线,两垂线的交点即为电子在磁场中做匀速圆周运
动时的圆心O,由勾股定理可得(R-h)2+d2=R2,整理知d=,而R
=,故d=,所以A错误.由带电粒子在有界磁场中做匀速圆周运
动,得t=,故B错误,C正确.又由于洛伦兹力和粒子运动的速度总垂直,对
粒子永远也不做功,故D错误.
答案:C
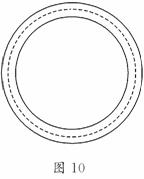
9.(2010·泰安模拟)如图10所示,为了科学研究的需要,
常常将质子(11H)和α粒子(24He)等带电粒子储存在圆环状
空腔中,圆环状空腔置于一个与圆环平面垂直的匀强磁场
(偏转磁场)中,磁感应强度为B.如果质子和α粒子在空腔
中做圆周运动的轨迹相同(如图中虚线所示),偏转磁场也
相同,则质子和α粒子在圆环状空腔中运动的动能EH和
Eα、运动的周期TH和Tα的大小关系是 ( )
A.EH=Eα,TH≠Tα B.EH=Eα,TH=Tα
C.EH≠Eα,TH≠Tα D.EH≠Eα,TH=Tα
解析:由=qvB可得:R==,T=,又因为∶=1∶1,
∶=2∶1,故EH=Eα,TH≠Tα.A项正确.
答案:A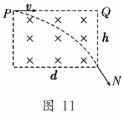
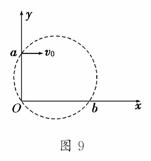
8.(2010·黄冈模拟)如图9所示,在平面直角坐标系中有一个
垂直于纸面向里的圆形匀强磁场,其边界过原点O和y轴
上的点a(0,L).一质量为m、电荷量为e的电子从a点以
初速度v0平行于x轴正方向射入磁场,并从x轴上的b点
射出磁场,此时速度方向与x轴正方向的夹角为60°.下列
说法中正确的是 ( )
A.电子在磁场中运动的时间为
B.电子在磁场中运动的时间为
C.磁场区域的圆心坐标(,)
D.电子在磁场中做圆周运动的圆心坐标为(0,-2L)
解析:由图可以计算出电子做圆周运动的半径为2L,故在磁场中运动的时间为t=
=,A错,B正确;ab是磁场区域圆的直径,故圆心坐标为(L,),电子
在磁场中做圆周运动的圆心为O′,计算出其坐标为(0,-L),所以C正确,D错、
误.
 答案:BC
答案:BC
7.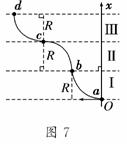 如图7所示,一个质量为m、电荷量为+q的带电粒子,不
如图7所示,一个质量为m、电荷量为+q的带电粒子,不
计重力,在a点以某一初速度水平向左射入磁场区域Ⅰ,沿
曲线abcd运动,ab、bc、cd都是半径为R的圆弧.粒子在
每段圆弧上运动的时间都为t.规定垂直于纸面向外的磁感应
强度为正,则磁场区域Ⅰ、Ⅱ、Ⅲ三部分的磁感应强度B随
x变化的关系可能是图8中的 ( )
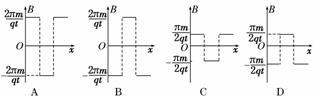
图8
解析:由左手定则可判断出磁感应强度B在磁场区域Ⅰ、Ⅱ、Ⅲ内磁场方向分别为
向外、向里、向外,在三个区域中均运动圆周,故t=,由于T=,求得B=.
只有C选项正确.
 答案:C
答案:C
6.如图6所示,相距为d的水平金属板M、N的左侧
有一对竖直金属板P、Q,板P上的小孔S正对板Q
上的小孔O,M、N间有垂直于纸面向里的匀强磁场,
在小孔S处有一带负电粒子,其重力和初速度均不
计,当滑动变阻器的滑片在AB的中点时,带负电粒
子恰能在M、N间做直线运动,当滑动变阻器的滑片
滑到A点后 ( )
A.粒子在M、N间运动过程中,动能一定不变
B.粒子在M、N间运动过程中,动能一定增大
C.粒子在M、N间运动过程中,动能一定减小
D.以上说法都不对
解析:当滑片向上滑动时,两个极板间的电压减小,粒子所受电场力减小,当滑到A
处时,偏转电场的电压为零,粒子进入此区域后做圆周运动.而加在PQ间的电压始
终没有变化,所以进入偏转磁场后动能也就不发生变化了.综上所述,A项正确.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com