
题目列表(包括答案和解析)
9.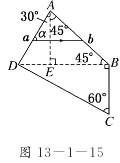 (2010·南通模拟)如图13-1-15所示,玻璃棱镜ABCD可
(2010·南通模拟)如图13-1-15所示,玻璃棱镜ABCD可
以看成是由ADE、ABE、BCD三个直角三棱镜组成.一束
频率为5.3×1014 Hz的单色细光束从AD面入射,在棱镜中
的折射光线如图中ab所示,ab与AD面的夹角α=60°.已知
光在真空中的速度c=3×108 m/s,玻璃的折射率n=1.5,求:
(1)这束入射光线的入射角多大?
(2)光在棱镜中的波长是多大?
(3)该束光线第一次从CD面出射时的折射角.(结果可用三角函数表示)
解析:(1)设光在AD面的入射角、折射角分别为θ1、θ2,θ2=30°
根据n=得sinθ1=nsinθ2=1.5×sin30°=0.75,
θ1=arcsin0.75.
(2)根据n=得
v== m/s=2×108 m/s,
根据v=λf得
λ== m≈3.77×10-7 m.
(3)光路如图所示,光线ab在AB面的入射角为45°,
设玻璃的临界角为C,则
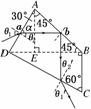
sinC==≈0.67
sin45°>0.67,因此光线ab在AB面会发生全反射
光线在CD面的入射角θ2′=θ2=30°
根据n=,光线在CD面的出射光线与法线的夹角θ1′=θ1=arcsin0.75.
答案:(1)arcsin0.75 (2)3.77×10-7 m (3)arcsin0.75
m
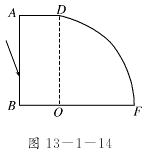
8.如图13-1-14所示为用某种透明材料制成的一块柱体
形棱镜的水平截面图,FD为圆周,圆心为O,光线从
AB面入射,入射角θ1=60°,它射入棱镜后射在BF面
上的O点并恰好不从BF面射出.
(1)画出光路图;
(2)求该棱镜的折射率n和光线在棱镜中传播的速度大小v(光在真空中的传播速度
c=3.0×108 m/s).
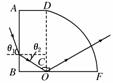 解析:(1)光路图如图所示.
解析:(1)光路图如图所示.
(2)设光线在AB面的折射角为θ2,折射光线与OD的夹角为C,
则n=.
由题意,光线在BF面恰好发生全反射,sinC=,由图可知,
θ2+C=90°
联立以上各式解出n≈1.3(或)
又n=,故解出v≈2.3×108 m/s(或×108 m/s).
答案:(1)见解析图
(2)1.3(或) 2.3×108 m/s(或×108 m/s)
7.(2010·苏南模拟)一台激光器,它的功率为P,如果它发射出的单色光在空气中的波
长为λ.
(1)它在时间t内辐射的光能为__________,如果已知这束单色光在某介质中的传播
速度为v,那么这束单色光从该介质射向真空发生全反射的临界角为__________.
(2)由于激光是亮度高、平行度好、单色性好的相干光,所以光导纤维中用激光作为
信息高速传输的载体.要使射到粗细均匀的圆形光导纤维一个端面上的激光束都能
从另一个端面射出,而不会从侧壁“泄漏”出来,光导纤维所用材料的折射率至少
应为多大?
解析:(1)激光器t时间内发出的光能W=Pt
由n=,sinC=,则C=arcsin.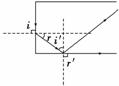
(2)设激光束在光导纤维端面的入射角为i,折射角为r,折射
光线射向侧面时的入射角为i′,折射角为r′,如图所示.
由折射定律:n=,
由几何关系:r+i′=90°,sinr=cosi′.
由全反射临界角的公式:
sini′=,
cosi′= ,
要保证从端面射入的任何光线都能发生全反射,应有i=r′=90°,sini=1.故
n===,
解得n=,故光导纤维的折射率至少应为.
 答案:(1)Pt arcsin (2)
答案:(1)Pt arcsin (2)
6.如图13-1-13所示,巡查员站立于一空的贮液池边,检查池角出液口的安全情况.已
知池宽为L,照明灯到池底的距离为H,若保持照明光束方向不变,向贮液池中注入
某种液体,当液面高为时,池底的光斑距离出液口.
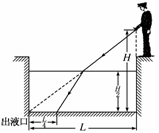
图13-1-13
(1)试求:当液面高为H时,池底的光斑到出液口的距离x.
(2)控制出液口缓慢地排出液体,使液面以vh的速率匀速下降,试求池底的光斑移动
的速率vx.
解析:(1)作出光路图如图所示.
由几何关系知:
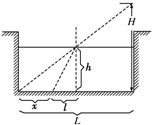 =①
=①
由折射定律:
=n· ②
代入h=、l=得:
n= ③
联立①②③式得x=·h.
当h=H时,解得x=.
(2)由x=·h知,Δx=·Δh,则
=·,即vx=·vh.
答案:(1) (2)·vh
5.(2009·海南高考)如图13-1-12所示,一透明半圆柱体折射率为n=2,半径为R,
长为L.一平行光束从半圆柱体的矩形表面垂直射入,从部分柱面有光线射出.求该
部分柱面的面积S.
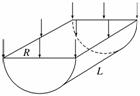
图13-1-12
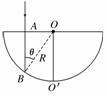 解析:半圆柱体的横截面如图所示,OO′为半径.设从A
解析:半圆柱体的横截面如图所示,OO′为半径.设从A
点入射的光线在B点处恰好满足全反射条件,由折射定律有
sinθ=
式中,θ为全反射临界角.由几何关系得
∠O′OB=θ
S=2RL·∠O′OB
代入题所给条件得
S=RL.
答案:RL
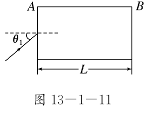
4.折射率为n、长度为L的玻璃纤维置于空气中,若从A
端射入的光线能在玻璃纤维中发生全反射,最后从B
端射出,如图13-1-11所示,求:
(1)光在A面上入射角的最大值.
(2)若光在纤维中恰能发生全反射,由A端射入到从B端射出经历的时间是多少?
解析:
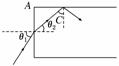 (1)光路图如右图所示,要在纤维中发生全反射,
(1)光路图如右图所示,要在纤维中发生全反射,
其临界角C有sinC=
折射角θ2=90°-C
所以cosθ2=,sinθ2=
由折射定律:sinθ1=nsinθ2=
θ1=arcsin.
(2)光在纤维中传播的速度v=(c为光在真空中传播的速度)
光在沿纤维轴线方向上的速度分量
v1=vcosθ2==
所用时间:t==.
答案:(1)arcsin (2)
3.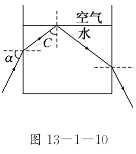 (2009·山东高考)一束单色光由左侧射入盛有清水的薄壁圆
(2009·山东高考)一束单色光由左侧射入盛有清水的薄壁圆
柱形玻璃杯,图13-1-10所示为过轴线的截面图,调整
入射角α,使光线恰好在水和空气的界面上发生全反射.已
知水的折射率为,求sinα的值.
解析:当光线在水面发生全反射时,有
sinC= ①
当光线从左侧射入时,由折射定律有
=n ②
联立①②式,代入数据可得sinα=.
 答案:
答案:
2.(2009·广东高考)在阳光照射下,充满雾气的瀑布上方常常会出现美丽的彩虹.彩虹
是太阳光射入球形水珠经折射、内反射、再折射后形成的.光的折射发生在两种不
同介质的________上,不同的单色光在同种均匀介质中________不同.
答案:界面 折射率
1.2009年10月6日,瑞典皇家科学院在斯德哥尔摩宣布,将2009年诺贝尔物理学奖
授予英国华裔科学家高锟以及美国科学家威拉德·博伊尔和乔治·史密斯.高锟在“有
关光在纤维中的传输以用于光学通信方面”取得了突破性的成就.若光导纤维是由
内芯和包层组成,下列说法正确的是 ( )
A.内芯和包层折射率相同,折射率都大
B.内芯和包层折射率相同,折射率都小
C.内芯和包层折射率不同,包层折射率较大
D.内芯和包层折射率不同,包层折射率较小
解析:为了使光线不射出来,必须利用全反射,而发生全反射的条件是光从折射率
较大的光密介质进入折射率较小的光疏介质.且入射角大于等于临界角,因此,内
芯的折射率应大于包层的折射率,故选项D正确.
答案:D
8.一般认为激光器发出的是频率为ν的“单色光”.实际上它的频率并不是真正单一
的.激光频率ν是它的中心频率,它所包含的频率范围是Δν(也称频率宽度).如图
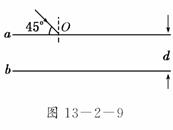
13-2-9所示,让单色光照射到薄膜表面a,一部分光从前表面反射
回来(这部分光称为甲光),其余的光进入薄膜内部,其中的一小部分光从薄膜后表面
b反射回来,再从前表面折射出(这部分光称为乙光),甲、乙这两部分光相遇叠加而
发生干涉,称为薄膜干涉,乙光与甲光相比,要在薄膜中多传播一小段时间Δt.理论
和实践都证明,能观察到明显稳定的干涉现象的条件是:Δt的最大值Δtm与Δν的乘
 积近似等于1,即只有满足Δtm·Δν≈1才会观察到明显稳
积近似等于1,即只有满足Δtm·Δν≈1才会观察到明显稳
定的干涉现象.
已知
某红宝石激光器发出的激光频率ν=4.32×1014 Hz,它的
频率宽度Δν=8.0×109 Hz.让这束激光由空气斜射到折
射率n=的薄膜表面,入射时与薄膜表面成45°角,如
图13-2-9所示.
(1)求从O点射入薄膜中的光的传播方向及速率.
(2)估算在如图13-2-9所示的情况下,能观察到明显稳定干涉现象的薄膜的最大厚
度dm.
解析:(1)设从O点射入薄膜中的光线的折射角为r,根据折射定律有:n=,
即sinr==
所以r=30°.
光在薄膜中的传播速度v=c/n≈2.12×108 m/s.
(2)乙光在薄膜中经历的路程x=
乙光通过薄膜所用时间Δt==
当Δt取最大值Δtm时,对应的薄膜厚度最大,
又因Δtm·Δν≈1,所以≈.
解得:dm≈1.15×10-2 m.
答案:(1)折射角为30°,速度大小为2.12×108 m/s
(2)1.15×10-2 m
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com