1．在用插针法测定玻璃砖的折射率的实验中，甲、乙、丙三位同学在纸上画出的界面

aa′、bb′与玻璃砖位置的关系分别如图实－1－8①、②和③所示，其中甲、丙两

同学用的是矩形玻璃砖，乙同学用的是梯形玻璃砖．他们的其他操作均正确，且均

以aa′、bb′为界面画光路图．

图实－1－8

(1)甲同学测得的折射率与真实值相比________(填“偏大”“偏小”或“不变”)．

(2)乙同学测得的折射率与真实值相比________(填“偏大”“偏小”或“不变”)．

(3)丙同学测得的折射率与真实值相比________．

解析：用图①测定折射率时，玻璃中折射光线偏折大了，所以折射角增大，折射率

减小；用图②测折射率时，只要操作正确，与玻璃砖形状无关；用图③测折射率时，

无法确定折射光线偏折的大小，所以测得的折射率可大、可小、可不变．

答案：(1)偏小　(2)不变　(3)可能偏大、可能偏小、可能不变

5．(1)某同学设计了一个测定激光波长的实验装置如图实－2－12所示，激光器发出一

束直径很小的红色激光进入一个一端装有双缝、另一端装有感光片的遮光筒，感光

片的位置上出现一排等距的亮线．

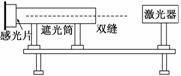
图实－2－12

这个现象说明激光具有________性．

(2)某同学在做“用双缝干涉测光的波长”的实验时，第一次分划板中心刻线对齐A

条纹中心时如图实－2－13甲所示，游标卡尺的示数如图丙所示；第二次分划板中心

刻线对齐B条纹中心线时如图乙所示，游标卡尺的读数如图丁所示．已知双缝间距

为0.5 mm，从双缝到屏的距离为 1 m，则图丙中游标卡尺的示数为________mm，

图丁中游标卡尺的示数为________ mm.实验时测量多条干涉条纹宽度的目的是

________________，所测光波的波长为________ m．(保留两位有效数字)

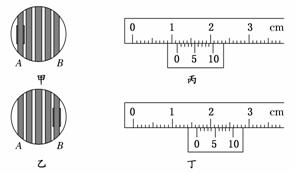
图实－2－13

解析：(1)此现象说明激光具有相干性．

(2)图丙读数11.5 mm，图丁读数16.7 mm

实验时测量多条干涉条纹宽度目的是减小测量的偶然误差．

由公式Δx＝λ得

λ＝＝ m

＝6.5×10^－7 m.

答案：(1)相干　(2)11.5　16.7　减小测量的偶然误差　6.5×10^－7

4．在利用双缝干涉测光波波长时，首先调节光源、滤光片、单缝和双缝的中心均位于

遮光筒的中心轴线上，并使单缝和双缝竖直并且互相平行，当屏上出现了干涉图样

后，用测量头上的游标卡尺去测量，转动手轮，移动分划板使分划中心刻线与某条

明纹中心对齐时(如图实－2－11A所示)将此明纹记为1，然后再转动手轮，分划板中

心刻线向右移动，依次经过2,3……等明纹，最终与明纹6中心对齐，分划板中心刻

线与明纹1和明纹6对齐时游标卡尺示数分别如图实－2－11中B、C所示(游标卡

尺为10分度)，则图B对应的读数为________m，图C对应的读数为________m．用

刻度尺量得双缝到屏的距离为60.00 cm，由双缝上标示获知双缝间距为0.2 mm，则

发生干涉的光波波长为________m.

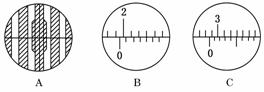
图实－2－11

在实验中，若经粗调后透过测量头上的目镜观察，看不到明暗相间的条纹，只看到

一片亮区，造成这种情况的最可能的原因是_________________________________．

解析：图B对应读数为1.94×10^－2 m

图C对应读数为2.84×10^－2 m

根据公式Δx＝λ得

λ＝＝ m

＝6.00×10^－7 m

若粗调后看不到干涉条纹，只看到一片亮区，则最可能的原因是单缝与双缝不平行．

答案：1.94×10^－2　2.84×10^－2　6.00×10^－7　单缝与双缝不平行

1．180 mm(1.179 mm-1.181 mm均正确)．

相邻两条亮(暗)纹间的距离：

Δx′＝＝ mm＝0.320 mm

由公式Δx′＝λ得

λ＝＝ mm＝4.8×10^－4 mm.

答案：1.180(1.179-1.181 均正确)　4.8×10^－4 mm

3．(2010·青岛模拟)某次实验时，该同学调节分划板的位置，使分

划板中心刻线对齐某亮纹的中心，如图实－2－10所示，此时螺

旋测微器的读数为________mm.转动手轮，使分划线向一侧移动

到另一条亮纹的中心位置，再次从螺旋测微器上读数．若实验测

得4条亮纹中心间的距离为Δx＝0.960 mm，已知双缝间距为 d＝1.5 mm，双缝到屏

的距离为L＝1.00 m，则对应的光波波长λ应为多少？

解析：螺旋测微器的读数为

2．利用双缝干涉测光的波长的实验中，双缝间距d＝0.4 mm，双缝到光屏间的距离l

＝0.5 m，用某种单色光照射双缝得到干涉条纹如图实－2－9所示，分划板在图中A、

B位置时游标卡尺读数也由图中所给出，则：

图实－2－9

(1)分划板在图中A、B位置时游标卡尺读数分别为x_A＝________mm，x_B＝

________mm，相邻两条纹间距Δx＝________mm；

(2)波长的表达式λ＝________(用Δx、l、d表示)，该单色光的波长λ＝________m；

(3)若改用频率较高的单色光照射，得到的干涉条纹间距将________(填“变大”、

“不变”或“变小”)．

解析：(1)游标卡尺读数时：一要注意精确度，二要注意读数时主尺读数应为游标尺

零刻度线所对主尺位置的读数；三要注意单位，无论是主尺读数还是游标尺读数都

要以mm为单位读取．本题中还要注意主尺上的数字的单位是cm，不是mm.

由图可知x_A＝11.1 mm，x_B＝15.6 mm，

Δx＝×(15.6－11.1) mm＝0.75 mm.

(2)由Δx＝λ得λ＝Δx＝×0.75×10^－3 m＝6.0×10^－7 m.

(3)由Δx＝λ可知，波长越长的光，干涉条纹间距越大．根据频率、光速与波长的关

系可知，频率越大的光，波长越短，所以干涉条纹间距越小．

答案：(1)11.1　15.6　0.75

(2)Δx　6.0×10^－7　(3)变小

1．(2009·上海高考)如图实－2－8所示为双缝干涉的实验示意图，若要使干涉条纹的间

距变大，可改用波长更________(填：长、短)的单色光，或者使双缝与光屏之间的距

离________(填：增大，减小)．

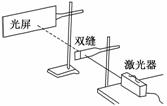
图实－2－8

解析：依据双缝干涉条纹间距规律Δx＝λ，可知要使干涉条纹的间距变大，需要改

用波长更长的单色光或增大双缝与屏之间的距离l.

答案：长　增大

2.0×10³ kg/m³，其中悬浮微粒的直径小于10^－7 m的称为“可吸入颗粒物”，对人体

的危害最大．北京地区出现上述沙尘暴时，设悬浮微粒中总体积的1/50为可吸入颗

粒物，并认为所有可吸入颗粒物的平均直径为5.0×10^－8 m，求1.0 cm³的空气中所

含可吸入颗粒物的数量是多少？(计算时可把可吸入颗粒物视为球形，计算结果保留

1位有效数字)

解析：出沙尘暴天气时，1 m³的空气中所含悬浮微粒的总体积为

V＝＝ m³＝2.9×10^－9 m³

那么1 m³中所含的可吸入颗粒物的体积为

V′＝＝5.8×10^－11 m³

又因为每一个可吸入颗粒物的体积为

V₀＝πd³≈6.54×10^－23 m³

所以1 m³中所含的可吸入颗粒物的数量

N＝≈8.9×10¹¹个

所以1.0 cm³的空气中所含可吸入颗粒物的数量为

N′＝N×1.0×10^－6＝8.9×10⁵个≈9×10⁵个．

　　 答案：9×10⁵个

12．(11分)由于生态环境的破坏，地表土裸露，大片土地沙漠化，加上春季干旱少雨，

所以近年来我国北方地区3、4月份扬尘天气明显增多．特别是2006年的3月26日

至28日，由于南下的冷空气所带来的大风，席卷了我国从新疆到沿海的北方大部分

地区，出现了罕见的沙尘暴天气．据环保部门测定，在北京地区沙尘暴严重时，最

大风速达到12 m/s，同时大量的微粒在空中悬浮．

沙尘暴使空气中的悬浮微粒的最高浓度达到5.8×10^－6 kg/m³，悬浮微粒的密度为

11．(12分)(1)随着科技的迅猛发展和人们生活水平的提高，下列问题一定能够实现或

完成的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．假如全世界60亿人同时数1 g水的分子个数，每人每小时可以数5000个，不间

断地数，则大约20年能数完(阿伏加德罗常数N_A取6.0×10²³个/mol)

B．热量可以从低温物体传到高温物体

C．热机的效率达到100 %

D．太阳能的利用普及到老百姓的日常生活中

(2)某学校研究性学习小组组织开展一次探究活动，想估算地球周围大气层空气的分

子个数和早晨同中午相比教室内的空气的变化情况．一学生通过网上搜索，查阅得

到以下几个物理量数据：地球的半径R＝6.4×10⁶ m，地球表面的重力加速度g＝9.8

m/s²，大气压强p₀＝1.0×10⁵ Pa，空气的平均摩尔质量M＝2.9×10^－2 kg/mol，阿伏加

德罗常数N_A＝6.0×10²³个/mol.另一个同学用温度计测出早晨教室内的温度是7℃，

中午教室内的温度是27℃.

①第一位同学根据上述几个物理量能估算出地球周围大气层空气的分子数吗？若

能，请说明现由；若不能，也请说明理由．

②根据上述几个物理量能否估算出中午跑到教室外的空气是早晨教室内的空气的几

分之几？

解析：(1)可估算需要10万年才能数完，所以A错；热力学第二定律告诉我们B正

确；热机是把内能转化为机械能的机器，根据热力学第二定律可知C错；太阳能的

开发和利用是人类开发新能源的主要思路，完全可以实现全民普及太阳能，所以D

正确．正确的答案为B、D.

(2)①能．因为大气压强是由大气重力产生的，

由p₀＝＝，得m＝

把查阅得到的数据代入上式得m≈5.2×10¹⁸kg

大气层空气的分子数为

N＝N_A＝×6.0×10²³个

≈1.1×10⁴⁴个

②可认为中午同早晨教室内的压强不变，根据等压变化规律＝，

将T₁＝280 K、T₂＝300 K，代入得

V₂＝V₁

故跑到室外的空气体积ΔV＝V₂－V₁＝V₁

所以跑到室外空气占早晨室内的比例为

＝＝.

答案：(1)B、D　(2)①能，理由见解析　②