
题目列表(包括答案和解析)
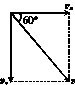
5. 如图甲所示,在高为1.5 m的光滑平台上有一个质量为2 kg的小球被一细线拴在墙上,球与墙之间有一根被压缩的轻质弹簧.当细线被烧断时,小球被弹出,小球落地时的速度方向与水平方向成60°角.求弹簧被压缩时具有的弹性势能.(取g=10 m/s2)
如图甲所示,在高为1.5 m的光滑平台上有一个质量为2 kg的小球被一细线拴在墙上,球与墙之间有一根被压缩的轻质弹簧.当细线被烧断时,小球被弹出,小球落地时的速度方向与水平方向成60°角.求弹簧被压缩时具有的弹性势能.(取g=10 m/s2)
解析:设小球落地前瞬间的速度为v,将v沿水平和竖直方向正交分解,如图乙所示,有:
 vy== m/s
vy== m/s
v==2 m/s
对于细线被烧断后的过程,由动能定理,有:
mgh+W弹=mv2-0
解得:W弹=10 J
弹簧被压缩时具有的弹性势能等于细线被烧断后弹簧对小球做的功,即Ep=W弹=10 J.
答案:10 J
4. 在盛水的一个杯子里有一木块,开始时木块被一根细绳拴住而完全没入水中,如图所示,整个装置与外界绝热,断开细绳,则木块将浮在水面上,最后达到平衡,在这一过程中,水、杯子和木块组成的系统( )
在盛水的一个杯子里有一木块,开始时木块被一根细绳拴住而完全没入水中,如图所示,整个装置与外界绝热,断开细绳,则木块将浮在水面上,最后达到平衡,在这一过程中,水、杯子和木块组成的系统( )
A.内能增大 B.内能减小
C.内能不变 D.条件不足,无法判断
解析:断开细绳后木块上升至水面,木块原来所处的位置被水填充,故水与木块组成的系统重心下降、重力势能减小.由能的转化和守恒定律知,系统的内能增大.
答案:A
3. 如图所示,M、N是固定的半圆形轨道的两个端点,轨道半径为R,一个质量为m的小球从M点正上方高为H处自由落下,正好沿切线进入轨道,M、N两点等高,小球离开N点后能上升的最大高度为.不计空气阻力,小球在此过程中克服半圆轨道摩擦力做的功为W;小球到最高点后又落回半圆轨道,向左侧滑动.则下列说法正确的是( )
如图所示,M、N是固定的半圆形轨道的两个端点,轨道半径为R,一个质量为m的小球从M点正上方高为H处自由落下,正好沿切线进入轨道,M、N两点等高,小球离开N点后能上升的最大高度为.不计空气阻力,小球在此过程中克服半圆轨道摩擦力做的功为W;小球到最高点后又落回半圆轨道,向左侧滑动.则下列说法正确的是( )
A.W=mgH,小球恰好能向左滑至M点
B.W=mgH,小球能向左滑出M点并继续上升一定高度
C.W<mgH,小球恰好能向左滑至M点
D.W<mgH,小球能向左滑出M点并继续上升一定高度
解析:小球从H高处下落经轨道后又上升至H高处的过程,由动能定理有:
mg(H-)-W=0
得:W=mgH
设小球再次落下后向左滑至M点时的速度为vM,由动能定理:mg-W′=mv
又因为向左滑过半圆轨道时经过每一点的速率都小于向右滑过时的速率,故小球对半圆轨道的压力以及半圆轨道对小球的摩擦力都小于前次向右滑过轨道该处的数值,可得W′<W,vM>0,即小球能滑出M点后又继续上升一定高度.
答案:B
2. 一块长木板B放在光滑的水平面上,在B上放一物体A,现以恒定的水平外力F拉B,由于A、B间摩擦力的作用,A将在B上滑动,如图所示.以地面为参考系,A、B都向前移动一段距离,在此过程中( )
一块长木板B放在光滑的水平面上,在B上放一物体A,现以恒定的水平外力F拉B,由于A、B间摩擦力的作用,A将在B上滑动,如图所示.以地面为参考系,A、B都向前移动一段距离,在此过程中( )
A.外力F做的功等于A和B动能的增量
B.B对A的摩擦力所做的功等于A动能的增量
C.A对B的摩擦力所做的功等于B对A的摩擦力所做的功
D.外力F对B所做的功等于B动能的增量与B克服摩擦力做的功之和
错解:由动能定理可得A正确.在物体A受的力中,只有B对A的摩擦力做了功,故B正确.作用力与反作用力做功大小相等,方向相反,故C正确.F对B做的功应等于B动能的增量减去B克服摩擦力做的功,故D错误.
剖析:从功能关系的角度来说,A、B组成的系统中还有内能产生,故WF=ΔEkA+ΔEkB+ΔQ.从动能定理的角度来说,A、B动能的增量应为所有力做功的总和,包括一对滑动摩擦力,而这对滑动摩擦力做的功之和并不为0,故A错误.由动能定理可知,B正确.一对作用力与反作用力可以同时做正功,也可同时做负功,还可……题中所述过程中,两物体在摩擦力作用下的位移不相等,故C错误.
正解:对于A,WBA=ΔEkA,故B正确.
设B克服摩擦力做的功为Wf,由动能定理得:
WF-Wf=ΔEkB
即:WF=ΔEkB+Wf.
故D正确.
答案:BD
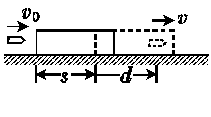
1.如图所示,一木块放在光滑水平面上,一子弹水平射入木块中,射入的深度为d,平均阻力为f.设木块运动s远时开始匀速前进,下列判断正确的是( )
 A.fs量度子弹损失的动能
A.fs量度子弹损失的动能
B.f(s+d)量度子弹损失的动能
C.fd量度子弹损失的动能
D.fd量度子弹、木块系统总动能的损失
解析:对木块运用动能定理有:fs=ΔEk1
对子弹运用动能定理有:-f(s+d)=ΔEk2
对系统运用动能定理有:-fd=ΔEk3
故选项B、D正确.
答案:BD
12.(10分)检测一个最大阻值为5 Ω的滑动变阻器,可供使用的器材如下:
A.待测滑动变阻器Rx,全电阻约为5 Ω(电阻丝绕制紧密,匝数清晰可数)
B.电流表 (量程为0.6 A,内阻约为0.6 Ω);
(量程为0.6 A,内阻约为0.6 Ω);
C.电流表 (量程为3 A,内阻约为0.12 Ω);
(量程为3 A,内阻约为0.12 Ω);
D.电压表 (量程为15 V,内阻约为15
kΩ);
(量程为15 V,内阻约为15
kΩ);
E.电压表 (量程为3 V,内阻约为3
kΩ);
(量程为3 V,内阻约为3
kΩ);
F.滑动变阻器R(最大阻值为20 Ω);
G.直流电源E(电动势为3 V,内阻不计);
H.游标卡尺;
I.毫米刻度尺;
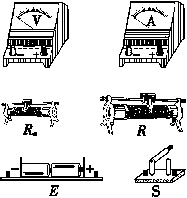 J.开关S、导线若干.
J.开关S、导线若干.
(1)用伏安法测定Rx的最大阻值,所选电流表为 (填“ ”或“
”或“ ”),所选电压表为 (填“
”),所选电压表为 (填“ ”或“
”或“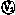 ”).
”).
(2)在虚线框中画出测量电路的原理图,并根据所画原理图将图甲中的实物连接成测量电路.
(3)为了进一步测量待测滑动变阻器电阻丝的电阻率,需要测量电阻丝的直径和总长度,在不破坏变阻器的前提下,请设计一个实验方案,写出所需器材及操作步骤,并给出直径和总长度的表达式.[2007年高考·山东理综卷]
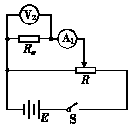
解析:(1)电源的电动势为3 V,故电压表应选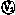 .若在待测滑动变阻器Rx两端加上3 V的电压,通过Rx的电流也仅约为0.6 A(I== A=0.6 A),故电流表应选
.若在待测滑动变阻器Rx两端加上3 V的电压,通过Rx的电流也仅约为0.6 A(I== A=0.6 A),故电流表应选 .
.
 (2)设计此题中的测量电路时,根据题中提供的可使用器材,要注意考虑两个方面的问题:①用伏安法测电阻时,电流表内外接法的选择;②将滑动变阻器接入电路时,分压式和限流式接法的选择.由于选用的电压表
(2)设计此题中的测量电路时,根据题中提供的可使用器材,要注意考虑两个方面的问题:①用伏安法测电阻时,电流表内外接法的选择;②将滑动变阻器接入电路时,分压式和限流式接法的选择.由于选用的电压表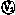 的内阻(约为3
kΩ)远大于待测滑动变阻器Rx的阻值(最大阻值为5
Ω),故采用电流表外接法.由于滑动变阻器的全电阻约为20 Ω,在此题中,采用分压式或限流式接法均能满足要求完成实验,故有两种方案可供选用.(答题时选用任一种均可)
的内阻(约为3
kΩ)远大于待测滑动变阻器Rx的阻值(最大阻值为5
Ω),故采用电流表外接法.由于滑动变阻器的全电阻约为20 Ω,在此题中,采用分压式或限流式接法均能满足要求完成实验,故有两种方案可供选用.(答题时选用任一种均可)
答案:(1)
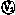
方案一 (2)电路原理图和对应的实物连接图如图乙所示
(3)需要的器材:游标卡尺、毫米刻度尺
主要操作步骤如下:
①数出变阻器线圈缠绕的匝数n;
②用毫米刻度尺(也可以用游标卡尺)测量所有线圈的排列长度l,可得电阻丝的直径d=;
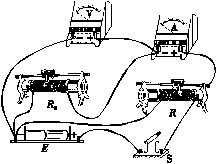 ③用游标卡尺测量变阻器线圈部分的外径D,可得电阻丝的总长度L=nπ(D-),也可以用游标卡尺测量变阻器瓷管部分的外径D,得电阻丝的总长度L=nπ(D+);
③用游标卡尺测量变阻器线圈部分的外径D,可得电阻丝的总长度L=nπ(D-),也可以用游标卡尺测量变阻器瓷管部分的外径D,得电阻丝的总长度L=nπ(D+);
④重复测量三次,求出电阻丝的直径和总长度的平均值.
方案二 (2)电路原理图和对应的实物连接图如图丙所示
(3)需要的器材:游标卡尺.
主要操作步骤如下:
 ①数出变阻器线圈缠绕的匝数n;
①数出变阻器线圈缠绕的匝数n;
②用游标卡尺测量变阻器线圈部分的外径D1和瓷管部分的外径D2,可得电阻丝的直径d=,电阻丝的总长度L=π(D1-D2);
③重复测量三次,求出电阻丝的直径和总长度的平均值.
11.(10分)有一根细而均匀的导电材料样品,截面为同心圆环,如图甲所示.此样品的长L约为3 cm,电阻约为100 Ω,已知这种材料的电阻率为ρ,且该样品的内径太小而无法直接测量.现提供以下实验器材:
 A.20等分刻度的游标卡尺;
A.20等分刻度的游标卡尺;
B.螺旋测微器;
C.电流表 (量程为50 mA,内阻r1=100 Ω);
(量程为50 mA,内阻r1=100 Ω);
D.电流表 (量程为100 mA,内阻r2约为40 Ω);
(量程为100 mA,内阻r2约为40 Ω);
E.滑动变阻器R1(0-10 Ω,额定电流为2 A);
F.直流电源E(电动势为12 V,内阻很小);
G.导电材料样品R2(长L约为3 cm,电阻R2约为100 Ω);
H.开关一只,导线若干.
请根据上述器材设计一个尽可能精确地测量该样品内径d的实验方案,回答下列问题:
(1)用游标卡尺测得该样品的长度如图乙所示,其示数L= mm;用螺旋测微器测得该样品的外径如图丙所示,其示数D= mm.

(2)在虚线框中画出设计的实验电路图,并标明所选器材的字母.
(3)用已知物理量和所测得的物理量的符号表示样品的内径d(写出推导过程).
答案:(1)30.35 3.204-3.206
 (2)电路如图丁所示
(2)电路如图丁所示
(3)设电流表 、
、 的示数分别为I1、I2,则:
的示数分别为I1、I2,则:
I1r1=(I2-I1)R2
根据电阻定律R2=ρ,由几何知识得:
S=
联立解得:d=.
10.(10分)要测量一长度为L、直径为D的电阻丝的阻值.
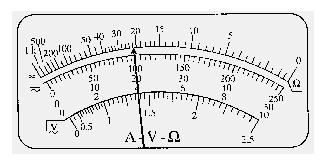
(1)用多用电表粗测该段电阻丝的阻值.用已经调零且选择旋钮指向欧姆挡“×10”位置的多用电表测量,发现指针偏转角度太大,这时应将选择旋钮指向欧姆挡“ ”位置;调零后测量,其表盘及指针所指位置如图所示,则此段电阻丝的电阻为 Ω.
(2)现在需要进一步精确测量该电阻丝的阻值.实验室备有下列器材:
A.量程为0.6 A、内阻为0.5 Ω的电流表;
B.量程为3 A、内阻为0.1 Ω的电流表;
C.量程为3 V、内阻为6 kΩ的电压表;
D.量程为15 V、内阻为30 kΩ的电压表;
E.阻值范围为1 kΩ的滑动变阻器R1;
F.阻值范围为50 Ω的滑动变阻器R2;
G.蓄电池的电动势为6 V,内阻很小;
H.开关一个,导线若干.
为使测量结果尽可能准确,电流表应选用 ,电压表应选用 ,滑动变阻器应选用 .(填仪器的代号)
若选择了最合适的器材,采用最恰当的实验电路进行实验测量,电流表的示数是I,电压表的示数是U,则该电阻丝的电阻率ρ= .
解析:(1)指针偏转角度太大,说明电阻值小,这时应使选择旋钮指向较小倍率,即欧姆挡的“×1”位置,多用电表欧姆挡的示数是表针示数乘以旋钮所在位置的倍率,所以电阻值为22×1 Ω=22 Ω.
(2)测量电路中的最大电流约为I==A<0.3 A,所以电流表应选择A,电压表应选择C,滑动变阻器应选择F.
由R=和R=ρ=ρ
联立解得:ρ=.
答案:(1)×1 22 (2)A C F
9.(10分)用下列器材测量一待测电阻Rx的阻值(900-1000 Ω):
电源E(具有一定内阻,电动势约为9.0 V);
电压表 (量程为1.5 V,内阻r1=750 Ω);
(量程为1.5 V,内阻r1=750 Ω);
电压表 (量程为5 V,内阻r2=2500 Ω);
(量程为5 V,内阻r2=2500 Ω);
滑动变阻器R(最大阻值约为100 Ω);
单刀单掷开关S,导线若干.
(1)测量中要求电压表的示数不小于其量程的,试画出测量电阻Rx的一种实验电路原理图(原理图中的元件要用题图中相应的英文字母标注).
(2)根据你所画的电路原理图在题给的实物图上连线.
(3)若电压表 的示数用U1表示,电压表
的示数用U1表示,电压表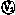 的示数用U2表示,则由已知量和测得量表示Rx的公式为: .
的示数用U2表示,则由已知量和测得量表示Rx的公式为: .
解析:(1)由于题目中要求电压表的示数不小于其量程的,所以必须采用分压式电路;而测量电阻Rx的值还必须知道Rx两端的电压和通过它的电流,由于电压表的内阻已知,所以可以用电压表充当电流表,可以选用下列两种中的任一种.
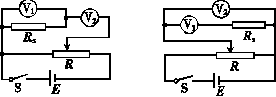
乙 丙
(2)实物连接图如图丁或戊所示.
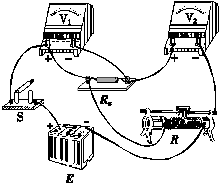
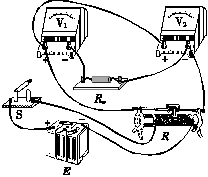
丁 戊
(3)采用乙图,则:=-
所以Rx=
采用丙图,则:=
所以Rx=r1.
答案:(1)如图乙或丙所示 (2)如图丁或戊所示
(3)Rx=或Rx=r1
8.(10分)需要测量电流表 的内阻r1,实验室中有下列器材可供选用:
的内阻r1,实验室中有下列器材可供选用:
|
器材(代号) |
规格 |
电流表 |
量程为10 mA,内阻r1待测(约40
Ω) |
电流表 |
量程为750 μA,内阻r2=600 Ω |
电压表 |
量程为15 V,阻值约为10 kΩ |
|
电源E |
电动势E=1.5 V,内阻可以忽略 |
|
滑动变阻器R1 |
阻值范围为0-20 Ω |
|
电阻箱R2 |
阻值范围为0-9999.9 Ω |
|
开关S两个 |
|
|
导线若干 |
|
在下列设计的四个电路图中,选出你认为最合适的在对应的横线上写出r1的表达式,并说明所用符号的物理意义;认为不合适的在对应的横线上写出理由.
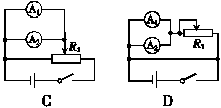
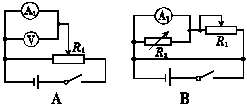
A图: ;
B图: ;
C图: ;
D图: .
解析:若选用 表测量电压,工作电压最大为量程的,示数误差会很大.由数据表可知,
表测量电压,工作电压最大为量程的,示数误差会很大.由数据表可知, 、
、 表满偏时电压相近,故可将
表满偏时电压相近,故可将 当电压表使用.
当电压表使用.
答案:A图: 的示数远小于量程,无法准确读数
的示数远小于量程,无法准确读数
B图: 、R1、R2都被短路
、R1、R2都被短路
 C图:r1=,I1、I2分别为
C图:r1=,I1、I2分别为 、
、 的示数
的示数
D图: 、
、 、R1被短路
、R1被短路
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com