1. (2010年南通调研)物体做平抛运动时，它的速度方向与水平方向夹角θ的正切值tan θ随时间t变化的图象如下图所示的(　)

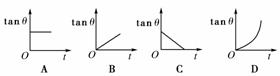
[解析]　根据平抛运动的规律，速度与水平方向的夹角θ的正切值为tan θ＝＝，为定值，所以tan θ与t成正比，选项B正确．

[答案]　B

14．(16分)

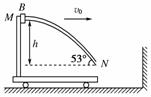
(2010年豫南九校联考)如右图所示，小车的刚性支架上固定一条刚性的轨道MN，轨道的左边是水平的，右边倾斜与水平面夹角为53°，两边通过一小段圆弧相连，小车、支架和轨道的总质量为2m，轨道M、N两点间的高度差为h.在轨道的最左边套一个质量为m的物块B，开始小车和物块一起以速度v₀沿光滑的水平面向右匀速运动，当小车与墙壁碰撞后，小车立即以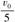的速度弹回，物块B开始沿着轨道滑行，当物块从轨道的N点滑出时，小车的速度刚好为零．求：

(1)小车与墙壁碰撞时，墙壁对小车的冲量；

(2)物块B从N点滑出时的速度；

(3)物块滑动过程中，轨道对物块做的功；

(4)物块滑动过程中，系统减少的机械能．(cos 53°=0.6)

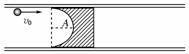
13．(16分)(2010石家庄二中)如图，是固定在水平面上的横截面为“”形的光滑长直导轨槽，槽口向上，槽内放置一金属滑块，滑块上有半径为R的半圆形光滑凹槽，金属滑块的宽度为2R，比“”形槽的宽度略小．现有半径为r(r<R)的金属小球以水平初速度v₀冲向滑块，从滑块上的半圆形槽口边缘进入．已知金属小球的质量为m，金属滑块的质量为3m，全过程中无机械能损失．求：

(1)当金属小球滑离金属滑块时，金属小球和金属滑块的速度各是多大？

(2)当金属小球经过金属滑块上的半圆形槽的底部A点时，对金属块的作用力是多大？

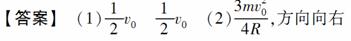
12.

(16分)(2010年豫南九校联考)如右图所示，小车的刚性支架上固定一条刚性的轨道MN，轨道的左边是水平的，右边倾斜与水平面夹角为53°，两边通过一小段圆弧相连，小车、支架和轨道的总质量为2m，轨道M、N两点间的高度差为h.在轨道的最左边套一个质量为m的物块B，开始小车和物块一起以速度v₀沿光滑的水平面向右匀速运动，当小车与墙壁碰撞后，小车立即以的速度弹回，物块B开始沿着轨道滑行，当物块从轨道的N点滑出时，小车的速度刚好为零．求：

(1)小车与墙壁碰撞时，墙壁对小车的冲量；

(2)物块B从N点滑出时的速度；

(3)物块滑动过程中，轨道对物块做的功；

(4)物块滑动过程中，系统减少的机械能．(cos 53°＝0.6)

[解析]　(1)对小车：由动量定理：I＝2m－2m(－v₀)＝，方向向左

(2)整个系统碰撞后水平方向动量守恒：mv₀－2mv₀＝mv_Ncos 53°，v_N＝v₀，速度方向与水平方向成53°，斜向右下．

(3)对物块B由动能定理：mgh+W＝－，得W＝－mgh.

(4)由动量守恒得：E_损＝2m²+mgh+mv－mv＝mgh+.

[答案]　(1)，方向向左

(2)v₀　速度方向与水平方向成53°，斜向右下．

(3)－mgh

(4)mgh+

11．(14分)

如右图所示，质量m₁＝0.3　 kg的小车静止在光滑的水平面上，车长L＝1.5 m，现有质量m₂＝0.2 kg可视为质点的物块，以水平向右的速度v₀＝2 m/s从左端滑上小车，最后在车面上某处与小车保持相对静止．物块与车面间的动摩擦因数μ＝0.5，取g＝10 m/s²，求：

(1)物块在车面上滑行的时间t；

(2)要使物块不从小车右端滑出，物块滑上小车左端的速度v′₀不超过多少．

[解析]　(1)设物块与小车共同速度为v，以水平向右为正方向，根据动量守恒定律有

m₂v₀＝(m₁+m₂)v①

设物块与车面间的滑动摩擦力为f，对物块应用动量定理有

－ft＝m₂v－m₂v₀②

又f＝μm₂g③

解得t＝

代入数据得t＝0.24 s．④

(2)要使物块恰好不从车面滑出，须使物块到车面最右端时与小车有共同的速度，设其为v′，则

m₂v′₀＝(m₁+m₂)v′⑤

由功能关系有

m₂v′＝(m₁+m₂)v′²+μm₂gL⑥

代入数据解得v′₀＝5 m/s

故要使物块不从小车右端滑出，物块滑上小车左端的速度v′₀不超过5 m/s.

[答案]　(1)0.24 s　(2)5 m/s

10.

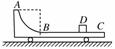
如右图所示，质量为M的小车静止在光滑的水平面上．小车上AB部分是半径为R的四分之一光滑圆弧，BC部分是粗糙的水平面．现把质量为m的小物体从A点由静止释放，m与BC部分间的动摩擦因数为μ.最终小物体与小车相对静止于B、C之间的D点，则B、D间的距离x随各量变化的情况是(　)

A．其他量不变，R越大x越大

B．其他量不变，μ越大x越大

C．其他量不变，m越大x越大

D．其他量不变，M越大x越大

[解析]　两个物体组成的系统水平方向的动量是守恒的，所以当两物体相对静止时，系统水平方向的总动量为零，则两物体最终会停止运动，由能量守恒有μmgx＝mgR，解得x＝，故选项A是正确的．

[答案]　A

9．如右图所示

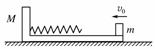
，长木板静止在光滑的水平面上，长木板的左端固定一个挡板，挡板上固定一个长度为L的轻质弹簧，长木板与挡板总质量为M，在木板的右端有一质量为m的铁块．现给铁块一个水平向左的初速度v₀，铁块向左滑行并与轻弹簧相碰，碰后返回恰好停在长木板的右端．根据以上条件可以求出的物理量是(　)

A．铁块与轻弹簧相碰过程中所具有的最大弹性势能

B．弹簧被压缩的最大长度

C．长木板运动速度的最大值

D．铁块与长木板间的动摩擦因数

[解析]　弹簧弹性势能最大时，铁块和木板的速度相等，在压缩弹簧的过程中两物体组成的系统动量守恒，摩擦力作为相互作用力，不知动摩擦因数，不能计算，但可根据功能关系选择整个过程，可计算摩擦力做功，再根据动量守恒计算两者速度相等时的速度，并计算过程中动能的减少量，即为弹簧弹性势能的最大值，A正确，因不知道弹簧劲度系数，故不能计算出弹簧的形变，B错误，而弹簧弹性势能达到最大后将释放出弹性势能，木板速度将继续增大，缺乏关于木板速度最大状态的参量， 故无法计算最大速度，C也错误，选A.

[答案]　A

8.

质量相等的5个物块在光滑水平面上间隔一定距离排成一直线，如右图所示，具有初动能E0的物块1向其他4个静止物块运动，依次发生碰撞，每次碰撞后不再分开，最后5个物块粘成一整体，这个整体的动能等于(　)

A．E₀　 　　　　　　　　　　　　　　　　　　　　　　 B.E₀

C.E₀　 　　　　　　　　　　　　　　　　　　　　　　 D.E₀

[解析]　物块1的动能E₀＝mv，得v₀＝，其初动量p₁＝mv₀＝.由5个物块组成的系统动量守恒，以碰撞前为初状态，碰后粘连在一起为末状态，有

p₁＝5mv

即＝5mv解得v＝

末动能E_k＝(5m)v²＝×(5m)²＝，选项C正确．

[答案]　C

7.

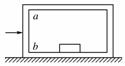
如右图所示，质量M＝50 kg的箱子，放在光滑水平面上，箱子中有一个质量m＝30 kg的铁块，铁块与箱子的左端ab壁相距s＝1 m，它一旦与ab壁接触后就不会分开，铁块与箱底间的摩擦可以忽略不计．用水平向右的恒力F＝10 N作用于箱子，2 s末立即撤去作用力，最后箱子与铁块的共同速度大小是(　)

A. m/s　 　　　　　　　　　　　　　　　　　　　　 B. m/s

C. m/s　 　　　　　　　　　　　　　　　　　　　　 D. m/s

[答案]　B

6.

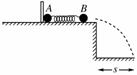
A、B两球之间压缩一根轻弹簧，静置于光滑水平桌面上．已知A、B两球质量分别为2m和m.当用板挡住A球而只释放B球时，B球被弹出落于距桌边距离为s的水平地面上，如右图所示．问当用同样的程度压缩弹簧，取走A左边的挡板，将A、B同时释放，B球的落地点距桌边距离为(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　 B.

C．s　 　　　　　　　　　　　　　　　　　　　　　　　 D.s

[解析]　当用板挡住小球A而只释放B球时，根据能量守恒有：E_p＝mv，根据平抛运动规律有：s＝v₀t.当用同样的程度压缩弹簧，取走A左边的档板，将A、B同时释放，设A、B的速度分别为v_A和v_B，则根据动量守恒和能量守恒有：2mv_A－mv_B＝0，E_p＝·2mv+mv，解得v_B＝v₀，B球的落地点距桌边距离为s′＝v_Bt＝s，D选项正确．

[答案]　D