12.

(2009年高考山东理综)如右图所示，某货场需将质量为m₁＝100 kg的货物(可视为质点)从高处运送至地面，为避免货物与地面发生撞击，现利用固定于地面的光滑四分之一圆轨道，使货物由轨道顶端无初速滑下，轨道半径R＝1.8 m．地面上紧靠轨道依次排放两块完全相同的木板A、B，长度均为l＝2 m，质量均为m₂＝100 kg，木板上表面与轨道末端相切．货物与木板间的动摩擦因数为μ₁，木板与地面间的动摩擦因数μ₂＝0.2.(最大静摩擦力与滑动摩擦力大小相等，取g＝10 m/s²)

(1)求货物到达圆轨道末端时对轨道的压力．

(2)若货物滑上木板A时，木板不动，而滑上木板B时，木板B开始滑动，求μ₁应满足的条件．

(3)若μ₁＝0.5，求货物滑到木板A末端时的速度和在木板A上运动的时间．

[解析]　(1)设货物滑到轨道末端时的速度为v₀，对货物的下滑过程，根据机械能守恒定律得

m₁gR＝m₁v①

设货物在轨道末端所受支持力的大小为F_N，根据牛顿第二定律得

F_N－m₁g＝m₁②

联立①②式，代入数据得

F_N＝3 000 N③

根据牛顿第三定律，货物对轨道的压力大小为3 000 N，方向竖直向下．

(2)若滑上木板A上时，木板不动，由受力分析得

μ₁m₁g≤μ₂(m₁+2m₂)g④

若滑上木板B时，木板B开始滑动，由受力分析得

μ₁m₁g>μ₂(m₁+m₂)g⑤

联立④⑤式，代入数据得

11.

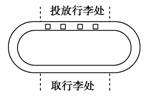
飞机场上运送行李的装置为一水平放置的环形传送带，传送带的总质量为M，其俯视图如右图所示．现开启电动机，传送带达稳定运行的速度v后，将行李依次轻轻放到传送带上．若有n件质量均为m的行李需通过传送带运送给旅客．假设在转弯处行李与传送带无相对滑动，忽略皮带轮、电动机损失的能量．求从电动机开启，到运送完行李需要消耗的电能为多少？

[解析]　设行李与传送带间的动摩擦因数为μ，则传送带与行李间由于摩擦产生的总热量Q＝nμmgΔs

由运动学公式得：Δs＝s_传－s_行＝vt－＝

又：v＝μgt，

联立解得：Q＝nmv²

由能量守恒得：E＝Q+Mv²+n×mv²

所以：E＝Mv²+nmv².

[答案]　Mv²+nmv²

10．在半径R＝5 000 km的某星球表面，宇航员做了如下实验，实验装置如图甲所示．竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成，将质量m＝0.2 kg的小球，从轨道AB上高H处的某点静止滑下，用力传感器测出小球经过C点时对轨道的压力F，改变H的大小，可测出相应的F大小，F随H的变化关系如图乙所示．求：

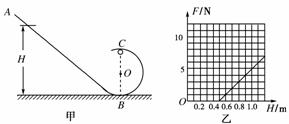
(1)圆轨道的半径；

(2)该星球的第一宇宙速度．

[解析]　(1)小球过C点时满足F+mg＝m

又根据mg(H－2r)＝mv

联立解得F＝H－5mg

由题图可知：H₁＝0.5 m时，F₁＝0；可解得r＝0.2 m

H₂＝1.0 m时F₂＝5 N；可解得g＝5 m/s²

(2)据m＝mg

可得v＝＝5×10³ m/s.

[答案]　(1)0.2 m　(2)5×10³ m/s

9.

(2010年华中科大附中)某同学经查阅资料得知：弹簧弹性势能的表达式为E_p＝kx²，其中k为弹簧的劲度系数，x为弹簧的形变量．为验证这个结论，他找来一根劲度系数未知的轻质弹簧和已知质量为m的物块，事先测出物块与水平面间的动摩擦因数μ的值．又查出当地重力加速度g的值．

(1)在测量实验所用弹簧的劲度系数k时，若只能选用一个测量仪器，则可以选择________．

(2)在测出弹簧的劲度系数k和物块与水平面间的动摩擦因数μ的值之后，按照图所示的方式进行仪器组装：弹簧左端固定在墙上，物块紧靠弹簧右端放置在水平面上，且与弹簧不拴接．

在弹簧处于原长的情况下，标记物块左侧边缘(即弹簧右端)的位置O；然后用水平力推物块，将弹簧压缩，标记弹簧压缩最短时物块左侧边缘的位置A；然后突然撤去推力，弹簧将物块推出，物块滑行一段距离后停下，标记此时物块左侧边缘的位置B.测得OA之间的距离为x₁，OB之间的距离为x₂.

在分析实验数据时，若算出________与________的值近似相等，便可视为成功验证了弹簧的弹性势能表达式．(且测得的物理量和已知物理量的符号表示)．

[答案]　(1)刻度尺(钟表同样得分)

(2)kx　μmg(x₁+x₂)

8．用起重机将一个质量为m的货物竖直向上以加速度a匀加速提升H米，在这个过程中，以下说法中正确的是(　)

A．起重机对物体的拉力大小为ma

B．物体的机械能增加了mgH

C．物体的动能增加了maH

D．物体的机械能增加了maH

[解析]　由动能定理可知，合外力对物体所做的功等于物体动能的变化，动能增加了F_合H＝maH，故选C.

[答案]　C

7.

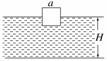
面积很大的水池，水深为H，水面上浮着一正方体木块，木块边长为a，密度为水的1/2，质量为m.开始时，木块静止，有一半没入水中，如右图所示．现用力将木块缓慢地压到池底．在这一过程中(　)

A．木块的机械能减少了mg

B．水池中水的机械能不变

C．水池中水的机械能增加了2mg

D．水池中水的机械能增加了2mg

[答案]　AD

6.

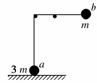
(2010年湖南师大附中)一不可伸长的轻绳两端各系小球a和b，跨在固定在同一高度的两根光滑水平细杆上，a球置于地面上，质量为3m，b球从水平位置静止释放，质量为m，如右图所示，当a球对地面压力刚好为零时，b球摆过的角度为θ，下列结论正确的是(　)

A．θ＝90°

B．θ＝45°

C．b球摆到最低点的过程中，重力对小球做功的瞬时功率先增大后减小

D．b球摆动到最低点的过程中，重力对小球做功的瞬时功率一直增大

[解析]　设b球的摆动半径为R，当摆过角度θ时的速度为v，对b球由动能定理：mgRsin θ＝mv²，此时绳子拉力为F_T＝3mg，在绳子方向由向心力公式：F_T－mgsin θ＝m，解得θ＝90°，A对B错；故b球摆动到最低点的过程中一直机械能守恒，竖直方向的分速度先从零开始逐渐增大，然后逐渐减小到零，故重力的瞬时功率P_b＝mgv_竖先增大后减小，C对D错．

[答案]　AC

5.

(2010年哈师大附中)在2008年北京奥运会上，俄罗斯著名撑杆跳运动员伊辛巴耶娃以5.05 m的成绩第24次打破世界纪录．右图为她在比赛中的几个画面，下列说法中正确的是(　)

A．运动员助跑阶段，运动员的动能增加

B．撑杆恢复形变时，其弹性势能全部转化为运动员的动能

C．在上升过程中运动员先对杆做负功后对杆做正功

D．运动员在上升过程中运动员的机械能守恒

[答案]　B

4.

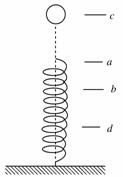
一轻弹簧竖直放置，下端固定在水平面上，上端处于a位置，一重球(可视为质点)无初速放在弹簧上端静止时，弹簧上端被压缩到b位置．现让重球从高于a位置的c位置沿弹簧中轴线自由下落，弹簧被重球压缩至d，以下关于重球下落运动过程中的正确说法是(不计空气阻力)(　)

A．整个下落a至d过程中，重球均做减速运动

B．重球落至b处获得最大速度

C．在a至d过程中，重球克服弹簧弹力做的功等于重球由c至d的重力势能的减小量

D．重球在b处具有的动能等于重球由c至b处减小的重力势能

[答案]　BC

3.

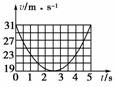
一个高尔夫球静止于平坦的地面上．在t＝0时球被击出，飞行中球的速率与时间的关系如右图所示．若不计空气阻力的影响，根据图象提供的信息可以求出(　)

A．高尔夫球在何时落地

B．高尔夫球可上升的最大高度

C．人击球时对高尔夫球做的功

D．高尔夫球落地时离击球点的距离

[解析]　因高尔夫球击出后机械能守恒，所以从题中图象看到，5 s末速率与初速率相等，说明球落回到地面，在2.5 s速率最小，为水平速度，根据运动的合成与分解可以算出竖直方向的初速度，这样就可以算出高尔夫球上升的最大高度和运动的时间，在水平方向高尔夫球匀速运动，可以求出射程，因高尔夫球的质量未知，不能算出人击球时对高尔夫球做的功，C项错误．

[答案]　ABD