1. 下列说法正确的是

　 A. 光波是-种概率波　　　 B. 光波是一种电磁波

　 C. 单色光从光密介质进入光疏介质时．光子的能量改变

　 D. 单色光从光密介质进入光疏介质时，光的波长不变

10．劈尖干涉是一种薄膜干涉，其装置如图1所示，将一块平板玻璃放置在另一平板玻璃之上，在一端夹入两张纸片，从而在两玻璃表面之间形成一个劈形空气薄膜。当光垂直入 　 射后，从上往下看到的干涉条纹如图2所示。

　干涉条纹有如下特点：(1)任意一条明条

　 纹或暗条纹所在位置下面的薄膜厚度相等；

　 (2)任意相邻明条纹和暗条纹所对应的薄膜厚度差

　 恒定。现若在图1装置中抽去一张纸片，则

　当光垂直入射到新的劈形空气薄膜后，从上

　 往下观察到的干涉条纹

　　 A．变疏　　　　　 B．变密　　　　　 C．不变　　　　　 D．消失

9．一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B。支架的两直角边长度分别为2l和l，支架可绕固定轴O在竖直平面内摩擦转动，如图所示。开始时OA边处于水平位置，由静止释放，则

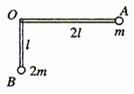　 　　 A．A球的最大速度为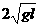

　　 B．A球速度最大时，两小球的总重力势能最小

　　 C．A球速度最大时，两直角边与竖直方向的夹角为45°

　　 D．A、B两球的最大速度之比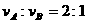

8．滑块以速率v₁靠惯性沿固定斜面由底端向上运动，当它回到出发点时速率为v₂，且v₂< v₁，若滑块向上运动的位移中点为A，取斜面底端重力势能为零，则

　 A．上升时机械能减小，下降时机械增大

　 B．上升时机械能减小，下降时机械能也减小

　 C．上升过程中动能和势能相等的位置在A点上方

　　 D．上升过程中动能和势能相等的位置在A点下方

7．光滑水平面上有一边长为l的正方形区域处在场强为E的匀强电场中，电场方向与正方形一边平行。一质量为m、带电量为q的小球由某一边的中点，以垂直于该边的水平初速v₀进入该正方形区域。当小球再次运动到该正方形区域的边缘时，具有的动能可能为

　 A．0　　　　　　　　　 B．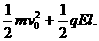

　 C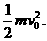．　　　　　　 D．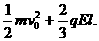

3．火星有两颗卫星，分别是火卫一和火卫二，它们的轨道近似为圆。已知火卫一的周期为7小时39分。火卫二的周期为30小时18分，则两颗卫星相比

　 A．火卫一距火星表面较近　　　　　　 B．火卫二的角速度较大

　 C．火卫一的运动速度较大　　　　　　 D．火卫二的向心加速度较大

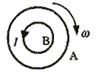　 4．两圆环A、B置于同一水平面上，其中A为均匀带电绝缘环，B为导体环，当A以如图所示的方向绕中心转动的角速度发生变化时，B中产生如图所示方向的感应电流。则

　 A．A可能带正电且转速减小

　 B．A可能带正电且转速增大

　 C．A可能带负电且转速减小

　 D．A可能带负电且转速增大

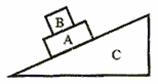　 5．物体B放在物体A上，A、B的上下表面均与斜面平行(如图)，当两者以相同的初速度靠惯性沿光滑固定斜面C向上做匀减速运动时，

　 A．A受到B的摩擦力沿斜面方向向上

　 B．A受到B的摩擦力沿斜面方向向下

　 C．A、B之间的摩擦力为零

　 D．A、B之间是否存在摩擦力取决于A、B表面的性质

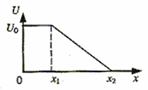　 6．某静电场沿x方向的电势分布如图所示，则

　 A．在0-x₁之间不存在沿x方向的电场

　 B．在0-x₁之间存在着沿x方向的匀强电场

　 C．在x₁-x₂之间存在着沿x方向的匀强电场

　 D．在x₁-x₂之间存在着沿x方向的非匀强电场

2．下列说法中正确的是

　 A．玛丽·居里首先提出原子的核式结构学说

　 B．卢瑟福在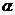粒子散射实验中发现了电子

　 C．查德威克在原子核人工转变的实验中发现了中子

　 D．爱因斯坦为解释光电效应的实验规律提出了光子说

1．下列说法正确的是

　 A．光的干涉和衍射现象说明光具有波动性

　 B．光的频率越大，波长越长

　 C．光的波长越大，光子的能量越大

　 D．光在真空中的传播速度为3.00×10⁸m/s

13.图示中滑块和小球的质量均为m，滑块可在水平放置的光滑固定导轨上自由滑动，小球与滑块上的悬点O由一不可伸长的轻绳相连，轻绳长为l.开始时，轻绳处于水平拉直状态，小球和滑块均静止.现将小球由静止释放，当小球到达最低点时，滑块刚好被一表面涂有黏性物质的固定挡板粘住，在极短的时间内速度减为零，小球继续向左摆动，当轻绳与竖直方向的夹角θ＝60° 时小球达到最高点.求：

(1)从滑块与挡板接触到速度刚好变为零的过程中，挡板阻力对滑块的冲量.

(2)小球从释放到第一次到达最低点的过程中，绳的拉力对小球做功的大小.[2008年高考·全国理综卷Ⅰ]

解析：(1)解法一　设小球摆至最低点时，滑块和小球的速度大小分别为v₁、v₂，对于滑块和小球组成的系统，由机械能守恒定律得：mv+mv＝mgl

同理，滑块被粘住后，对于小球向左摆动的过程，有：

mv＝mgl(1－cos 60°)

解得：v₁＝v₂＝

对于滑块与挡板接触的过程，由动量定理得：

I＝0－mv₁

挡板对滑块的冲量I＝－m，负号表示方向向左.

解法二　设小球摆至最低点时，滑块和小球的速度大小分别为v₁、v₂，由动量守恒定律得：

mv₁－mv₂＝0

对于小球向左摆动的过程，由机械能守恒定律得：

mv＝mgl(1－cos 60°)

解得：v₁＝v₂＝

对于滑块与挡板接触的过程，由动量定理有：

I＝0－mv₁

解得挡板对滑块的冲量为：

I＝－m，负号表示方向向左.

解法三　设小球摆至最低点时，滑块和小球的速度大小分别为v₁、v₂，由机械能守恒定律得：

mv+mv＝mgl

又由动量守恒定律得：

mv₁+m(－v₂)＝0

解得：v₁＝v₂＝

对于滑块与挡板接触的过程，由动量定理得：

I＝0－mv₁解得挡板对滑块的冲量为：

I＝－m，负号表示方向向左.

　解法四　由全过程的能量转换和守恒关系可得(滑块在碰撞时损失的能量等于系统机械能的减少量，等于滑块碰前的动能)：

ΔE＝mgl－mgl(1－cos 60°)＝mv²

解得滑块碰前的速度为：v＝

对于滑块与挡板接触的过程，由动量定理得：

I＝0－mv

解得挡板对滑块的冲量为：

I＝－m，负号表示方向向左.

(2)解法一　对小球下摆的过程，由动能定理得：

mgl+W＝mv

解得细绳对其做的功为：

W＝－mgl.

解法二　绳的张力对小球所做功的绝对值等于滑块在碰前的动能(或等于绳子的张力对滑块做的功)，则有：

W′＝mv或W′＝mv－0

解得：W＝－W′＝－mgl.

解法三　绳子的张力对小球做的功等于小球在全过程中的机械能的增量，取滑块所在高度的水平面为参考平面，有：

W＝(－mg·)－0＝－mgl(取水平位置为重力势能零点)

或W＝mgl(1－cos 60°)－mgl＝－mgl(取最低点为重力势能零点)

或W＝0－mg·＝－mgl(取小球运动到的最高点为重力势能零点).

解法四　对小球运动的全过程，由动能定理得：

W+mglcos 60°＝0或W+mg·＝0

解得：W＝－mgl.

解法五　考虑小球从水平位置到最低点的过程：

若滑块固定，绳子的张力对小球不做功，小球处于最低点时的速率v_球′＝(由mgl＝mv_球′²得到)

若滑块不固定，绳子的张力对小球做功，小球处于最低点时的速率v_球＝(v_球应由前面正确求得)

则绳子对小球做的功为：

W＝mv－mv_球′²＝－mgl.

答案：(1)－m，负号表示方向向左

(2)－mgl

12.如图甲所示，有一个竖直固定在地面的透气圆筒，筒中有一劲度系数为k的轻弹簧，其下端固定，上端连接一质量为m的薄滑块，圆筒内壁涂有一层新型智能材料--ER流体，它对滑块的阻力可调.起初，滑块静止，ER流体对其阻力为0，弹簧的长度为L.现有一质量也为m的物体从距地面2L处自由落下，与滑块碰撞后粘在一起向下运动.为保证滑块做匀减速运动，且下移距离为时速度减为0，ER流体对滑块的阻力须随滑块下移而变.试求(忽略空气阻力)：

(1)下落物体与滑块碰撞过程中系统损失的机械能.

(2)滑块向下运动过程中加速度的大小.

(3)滑块下移距离d时ER流体对滑块阻力的大小.

[2008年高考·重庆理综卷]

解析：(1)设物体自由下落的末速度为v₀，由机械能守恒定律有：

mgL＝mv

解得：v₀＝

设碰后共同速度为v₁，由动量守恒定律有：

2mv₁＝mv₀

解得：v₁＝

碰撞过程中系统损失的机械能为：

ΔE＝mv－×2mv＝mgL.

(2)设加速度的大小为a，有：2as＝v

解得：a＝.　　　　　　　　　　　　　　　　　　　　　　　　　 乙

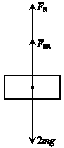
(3)设弹簧的弹力为F_N，ER流体对滑块的阻力为F_ER，滑块的受力分析如图乙所示，则有：

F_N+F_ER－2mg＝2ma

F_N＝kx

x＝d+

解得：F_ER＝mg+－kd.

答案：(1)mgL　(2)　(3)mg+－kd.